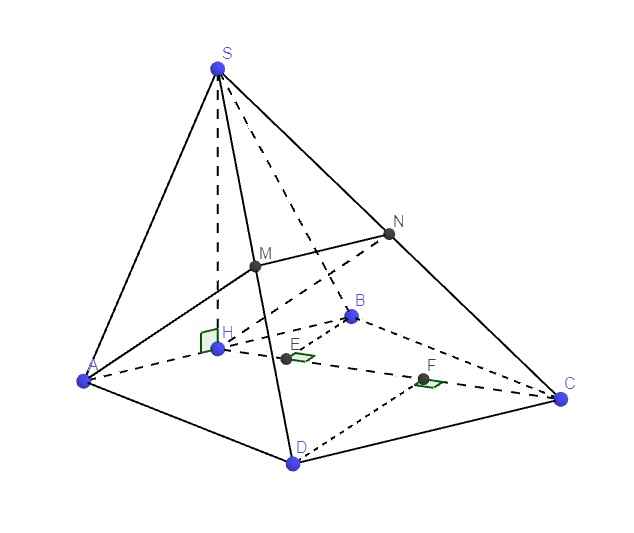
Tam giác SAB đều \(\Rightarrow SH\perp AB\)
Mà \(\left\{{}\begin{matrix}AB=\left(SAB\right)\cap\left(ABCD\right)\\\left(SAB\right)\perp\left(ABCD\right)\end{matrix}\right.\) \(\Rightarrow SH\perp\left(ABCD\right)\)
Gọi N là trung điểm SC \(\Rightarrow MN\) là đường trung bình tam giác SCD
\(\Rightarrow\left\{{}\begin{matrix}MN||CD\\MN=\dfrac{1}{2}CD\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}MN||AH\\MN=AH\end{matrix}\right.\) \(\Rightarrow AMNH\) là hbh
\(\Rightarrow AM||HN\Rightarrow AM||\left(SHC\right)\)
\(\Rightarrow d\left(AM;SC\right)=d\left(AM;\left(SHC\right)\right)=d\left(A;\left(SHC\right)\right)\)
Mặt khác H là trung điểm AB \(\Rightarrow d\left(A;\left(SHC\right)\right)=d\left(B;\left(SHC\right)\right)\)
Từ B kẻ \(BE\perp HC\Rightarrow BE\perp\left(SHC\right)\) (do \(SH\perp BE\))
\(\Rightarrow BE=d\left(B;\left(SHC\right)\right)\)
Hệ thức lượng: \(BE=\dfrac{BH.BC}{CH}=\dfrac{BH.BC}{\sqrt{BH^2+BC^2}}=\dfrac{a\sqrt{5}}{5}\)
b.
Từ D kẻ \(DF\perp HC\Rightarrow DF\perp\left(SHC\right)\) (do \(SH\perp DF\))
\(\Rightarrow DF=d\left(D;\left(SHC\right)\right)\)
\(DF=DC.cos\widehat{FDC}=DC.cos\widehat{BCH}=\dfrac{DC.BC}{CH}=\dfrac{DC.BC}{\sqrt{BC^2+BH^2}}=\dfrac{2a\sqrt{5}}{5}\)