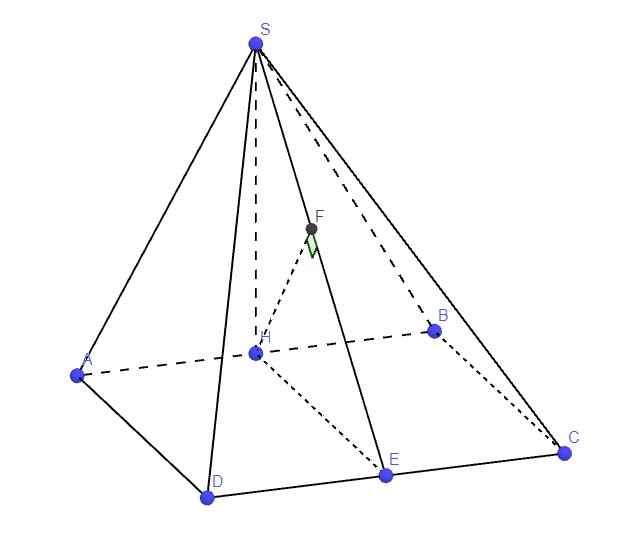
Do SAB là tam giác đều \(\Rightarrow SH\perp AB\)
Mà \(\left\{{}\begin{matrix}\left(SAB\right)\perp\left(ABCD\right)\\AB=\left(SAB\right)\cap\left(ABCD\right)\end{matrix}\right.\) \(\Rightarrow SH\perp\left(ABCD\right)\)
Gọi E là trung điểm CD, từ H kẻ \(HF\perp SE\) (F thuộc SE)
\(\left\{{}\begin{matrix}HE\perp CD\\SH\perp\left(ABCD\right)\Rightarrow SH\perp CD\end{matrix}\right.\) \(\Rightarrow CD\perp\left(SHE\right)\)
\(\Rightarrow CD\perp HF\)
\(\Rightarrow HF\perp\left(SCD\right)\Rightarrow HF=d\left(H;\left(SCD\right)\right)\)
\(HE=BC=a\) ; \(SH=\dfrac{a\sqrt{3}}{2}\) (trung tuyến tam giác đều cạnh a)
Hệ thức lượng:
\(HF=\dfrac{SH.HE}{\sqrt{SH^2+HE^2}}=\dfrac{a\sqrt{21}}{7}\)