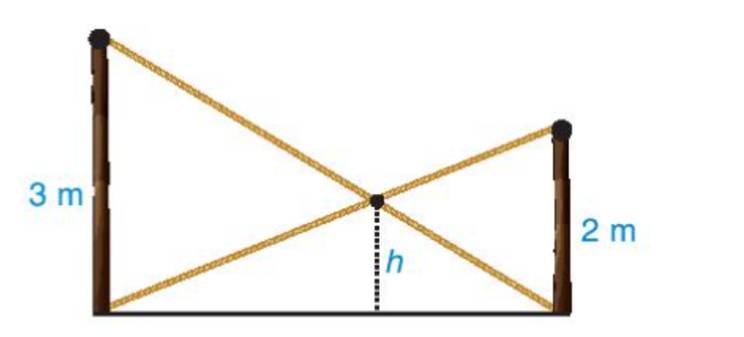
Có hai chiếc cột dựng thẳng đứng trên mặt đất với chiều cao lần lượt là 3m và 2m. Người ta nối hai sợi dây từ đỉnh cột này đến chân cột kia và hai sợi dây cắt nhau tại một điểm (H.9.25), hãy tính độ cao h của điểm đó so với mặt đất.
Những câu hỏi liên quan
Hai cột thẳng đứng của hai trại A và B cách nhau 8 mét .Từ một cái cọc ở chính giữa hai cột ,người ta đo được góc giữa các dây căng từ đỉnh hai cột của hai trại A và B đến cọc tạo với mặt đất lần lượt là 35 độ và 30 độ
a) tinh chiều cao mỗi trại ?
b) tại nào cao hơn và cao hơn bao nhiêu mét ?
Hai cột thẳng đứng của hai trại A và B (của lớp 9A và lớp 9B) cách nhau 8m. Từ một cái cọc ở chính giữa hai cột, người ta đo được góc giữa các dây căng từ đỉnh hai cột của hai trại A và B đến cọc tạo với mặt đất lần lượt là
35
°
và
30
°
. Hỏi trại nào cao hơn và cao hơn bao nhiêu mét?
Đọc tiếp
Hai cột thẳng đứng của hai trại A và B (của lớp 9A và lớp 9B) cách nhau 8m. Từ một cái cọc ở chính giữa hai cột, người ta đo được góc giữa các dây căng từ đỉnh hai cột của hai trại A và B đến cọc tạo với mặt đất lần lượt là 35 ° và 30 ° . Hỏi trại nào cao hơn và cao hơn bao nhiêu mét?
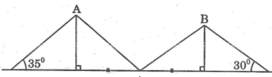
Chiều cao trại A là cạnh góc vuông đối diện với góc nhọn 35 ° , chiều cao trại B là cạnh góc vuông đối diện với góc nhọn 30 ° , cạnh kề với hai góc nhọn bằng nhau bằng 4m.
Chiều cao trại A là: 4.tg 35 ° ≈ 2,801 (m)
Chiều cao trại B là: 4.tg 30 ° ≈ 2,309 (m)
Trại A cao hơn trại B là: 2,801 – 2,309 = 0,492 (m)
Đúng 0
Bình luận (0)
Hai cột thẳng đứng của hai trại A và B , của lớp 9A và lớp 9B, cách nhau 8m. Từ một cái cọc ở chính giữa hai cột, người ta đo được góc giữa các dây căng từ đỉnh hai cột của hai trại A và B đến cọc tạo với mặt đất là 35 độ và 30 độ. Hỏi trại nào cao hơn và cao hơn bao nhiêu?
Chiều cao trại A là: 4.tan350≈ 2,801(m)
Chiều cao trại B là: 4.tan300 ≈ 2,309(m)
Trại A cao hơn trại B là: 2,801– 2,309 = 0,492(m)
Đúng 0
Bình luận (0)
Cổng Arch tại thành phố St Louis của Mỹ có hình dạng là một parabol (hình vẽ). Biết khoảng cách giữa hai chân cổng bằng 162m. Trên thành cổng, tại vị trí có độ cao 43m so với mặt đất (điểm M), người ta thả một sợi dây chạm đất (dây căng thẳng theo phương vuông góc với đất). Vị trí chạm đất của đầu sợi dây này cách chân cổng A một đoạn 10m. Giả sử các số liệu trên là chính xác. Hãy tính độ cao của cổng Arch (tính từ mặt đất đến điểm cao nhất của cổng). A. 175,6m B. 197,5m C. 210m D. 185,6m
Đọc tiếp
Cổng Arch tại thành phố St Louis của Mỹ có hình dạng là một parabol (hình vẽ). Biết khoảng cách giữa hai chân cổng bằng 162m. Trên thành cổng, tại vị trí có độ cao 43m so với mặt đất (điểm M), người ta thả một sợi dây chạm đất (dây căng thẳng theo phương vuông góc với đất). Vị trí chạm đất của đầu sợi dây này cách chân cổng A một đoạn 10m. Giả sử các số liệu trên là chính xác. Hãy tính độ cao của cổng Arch (tính từ mặt đất đến điểm cao nhất của cổng).
A. 175,6m
B. 197,5m
C. 210m
D. 185,6m
một cột buòm cao 60m được giữ cố định bỏi các sợi dây có một đầu buộc vào đỉnh cột, đầu kia buộc vào sàn tàu cách chân cột 25m . Tính chiều dài của sợi dây
Trên cánh đồng cỏ có 2 con bò được cột vào hai cây cộc khác nhau. Biết khoảng cách giữa 2 cọc là 5m, còn hai sợi dây buộc hai con bò lần lượt có chiều dài là 4m và 3m( không tính phần chiều dài dây buộc bò ). Tính diện tích mặt cỏ lớn nhất mà 2 con bò có thể ăn chung (làm tròn đến hàng phần nghìn). A. 6,642
m
2
B. 6,246
m
2
C. 4,624
m
2
D. 4,262 ...
Đọc tiếp
Trên cánh đồng cỏ có 2 con bò được cột vào hai cây cộc khác nhau. Biết khoảng cách giữa 2 cọc là 5m, còn hai sợi dây buộc hai con bò lần lượt có chiều dài là 4m và 3m( không tính phần chiều dài dây buộc bò ). Tính diện tích mặt cỏ lớn nhất mà 2 con bò có thể ăn chung (làm tròn đến hàng phần nghìn).
A. 6,642 m 2
B. 6,246 m 2
C. 4,624 m 2
D. 4,262 m 2
Đáp án A
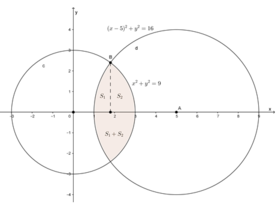
Ta giải bằng phương pháp gắn hệ tọa độ Oxy, với gốc tọa độ O chính là chỗ cây cộc buộc con bò có sợi dây dài 3m, trục Ox là đường nối 2 cây cộc buộc dây của 2 con bò, ta được như hình vẽ.
Khi đó con bò có sợi dây 3m có thể ăn cỏ trong hình tròn giới hạn bởi đường tròn có bán kính 3m và có phương trình đường tròn tâm O là
là đường phía trên trục hoành. Ta cũng có phần cỏ của con bò có sợi dây 4m bị hạn chế trong đường tròn có phương trình tâm A, bán kính 4 là
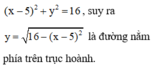
Giao điểm của 2 đường tròn này là nghiệm của hệ 2 pt đường tròn đó
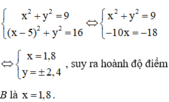
Ta chỉ cần tính phần diện tích phía trên trục hoành, phần dưới trục hoành có độ lớn cũng bằng như vậy. Từ B ta vẽ đường nét đứt vuông góc với Ox để chia đôi phần cần tính diện tích phía trên trục hoành, ta có
Đúng 0
Bình luận (0)
SGK Kết nối tri thức và cuộc sống
16 tháng 8 2023 lúc 18:16
Ở một con dốc lên cầu, người ta đặt một khung khống chế chiều cao, hai cột của khung có phương thẳng đứng và có chiều dài bằng 2,28 m. Đường thẳng nối hai chân cột vuông góc với hai đường mép dốc. Thanh ngang được đặt trên đỉnh hai cột. Biết dốc nghiêng 150 so phương nằm ngang. Tính khoảng cách giữa thanh ngang của khung và mặt đường (theo đơn vị mét và làm tròn kết quả đến chữ số thập phân thứ hai). Hỏi cầu này có cho phép xe cao 2,21 m đi qua hay không?
Đọc tiếp
Ở một con dốc lên cầu, người ta đặt một khung khống chế chiều cao, hai cột của khung có phương thẳng đứng và có chiều dài bằng 2,28 m. Đường thẳng nối hai chân cột vuông góc với hai đường mép dốc. Thanh ngang được đặt trên đỉnh hai cột. Biết dốc nghiêng 150 so phương nằm ngang. Tính khoảng cách giữa thanh ngang của khung và mặt đường (theo đơn vị mét và làm tròn kết quả đến chữ số thập phân thứ hai). Hỏi cầu này có cho phép xe cao 2,21 m đi qua hay không?
Gọi B là một điểm nằm trên thanh ngang và H là hình chiếu vuông góc xuống mặt dốc.
Vì dốc nghiêng 150 so với phương nằm ngang nên nên góc giữa cột và mặt phẳng dốc bằng 750
Khoảng cách từ B đến mặt phẳng dốc là:
\(BH=2.28\cdot sin75\simeq2,2\left(m\right)\)
=>Không cho phép xe cao 2,21m đi qua cầu
Đúng 0
Bình luận (0)
Một sợi cáp R được gắn vào một cột thẳng đứng ở vị trí cách mặt đất 14m. Một sợi cáp S khác cũng được gắn vào cột đó ở vị trí cách mặt đất 12m. Biết rằng hai sợi cáp trên cũng được gắn với mặt đất tại một vị trí cách chân cột 15m (Hình 18)a) Tính tan alpha , ở đó alpha là góc giữa hai sợi cáp trênb) Tìm góc alpha (làm tròn đến kết quả hàng đơn vị theo đơn vị độ)
Đọc tiếp
Một sợi cáp R được gắn vào một cột thẳng đứng ở vị trí cách mặt đất 14m. Một sợi cáp S khác cũng được gắn vào cột đó ở vị trí cách mặt đất 12m. Biết rằng hai sợi cáp trên cũng được gắn với mặt đất tại một vị trí cách chân cột 15m (Hình 18)
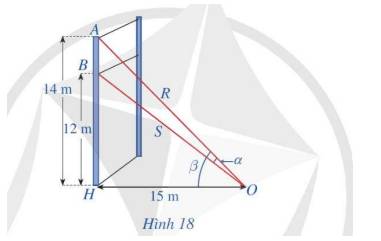
a) Tính \(\tan \alpha \), ở đó \(\alpha \) là góc giữa hai sợi cáp trên
b) Tìm góc \(\alpha \) (làm tròn đến kết quả hàng đơn vị theo đơn vị độ)
a) Ta có:
\(\begin{array}{l}\tan \widehat {AOB} = \frac{{AH}}{{HO}} = \frac{{14}}{{15}}\\\tan \beta = \frac{{BH}}{{HO}} = \frac{{12}}{{15}} = \frac{4}{5}\end{array}\)
Ta có: \(\tan \alpha = \tan \left( {\widehat {AOB} - \beta } \right) = \frac{{\tan \widehat {AOB} - \tan \beta }}{{1 + \tan \widehat {AOB.}\tan \beta }} = \frac{{\frac{{14}}{{15}} - \frac{4}{5}}}{{1 + \frac{{14}}{{15}}.\frac{4}{5}}} = \frac{{10}}{{131}}\)
b) \(\tan \alpha = \frac{{10}}{{131}} \Rightarrow \alpha \approx {4^o}\)
Đúng 0
Bình luận (0)
Hai cột thẳng đứng của hai trại A và B, của lớp 9A và lớp 9B, cách nhau 8m. Từ một cái cọc ở chính giữa hai cột, người ta đo được góc giữa các dây căng từ đỉnh hai cột của hai trại A và B đến cọc tạo với mặt đất lần lượt là 35^0 và 30^0 (h.23).
Hỏi trại nào cao hơn và cao hơn bao nhiêu mét ?
(Các kết quả tính độ dài, diện tích, các tỉ số lượng giác được làm tròn đến chữ số thập phân thứ ba và các kết quả tính góc được làm tròn đến phút)
Đọc tiếp
Hai cột thẳng đứng của hai trại A và B, của lớp 9A và lớp 9B, cách nhau 8m. Từ một cái cọc ở chính giữa hai cột, người ta đo được góc giữa các dây căng từ đỉnh hai cột của hai trại A và B đến cọc tạo với mặt đất lần lượt là \(35^0\) và \(30^0\) (h.23).
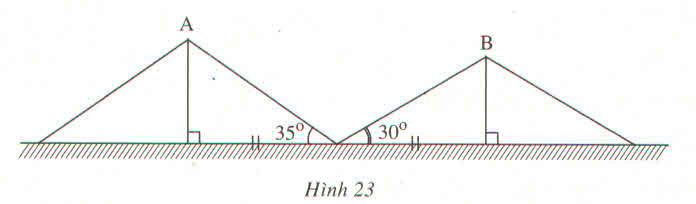
Hỏi trại nào cao hơn và cao hơn bao nhiêu mét ?
(Các kết quả tính độ dài, diện tích, các tỉ số lượng giác được làm tròn đến chữ số thập phân thứ ba và các kết quả tính góc được làm tròn đến phút)
