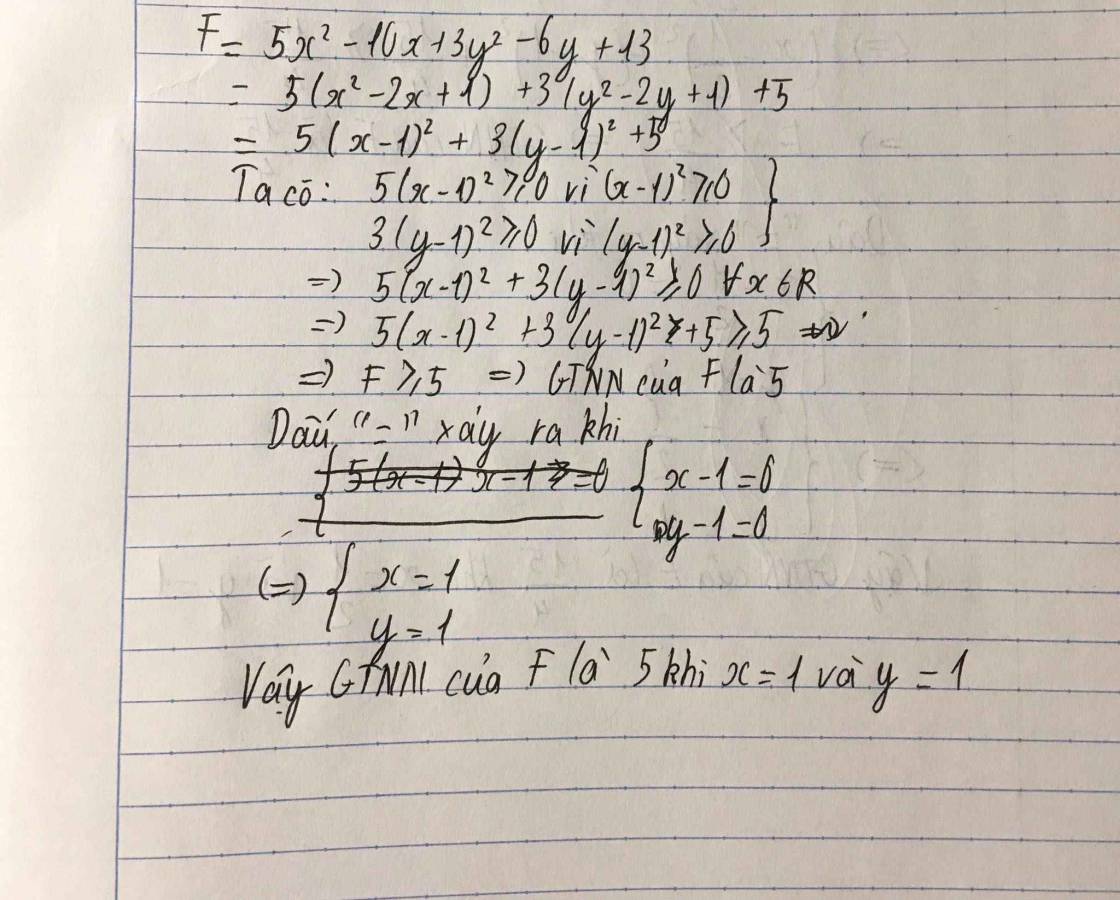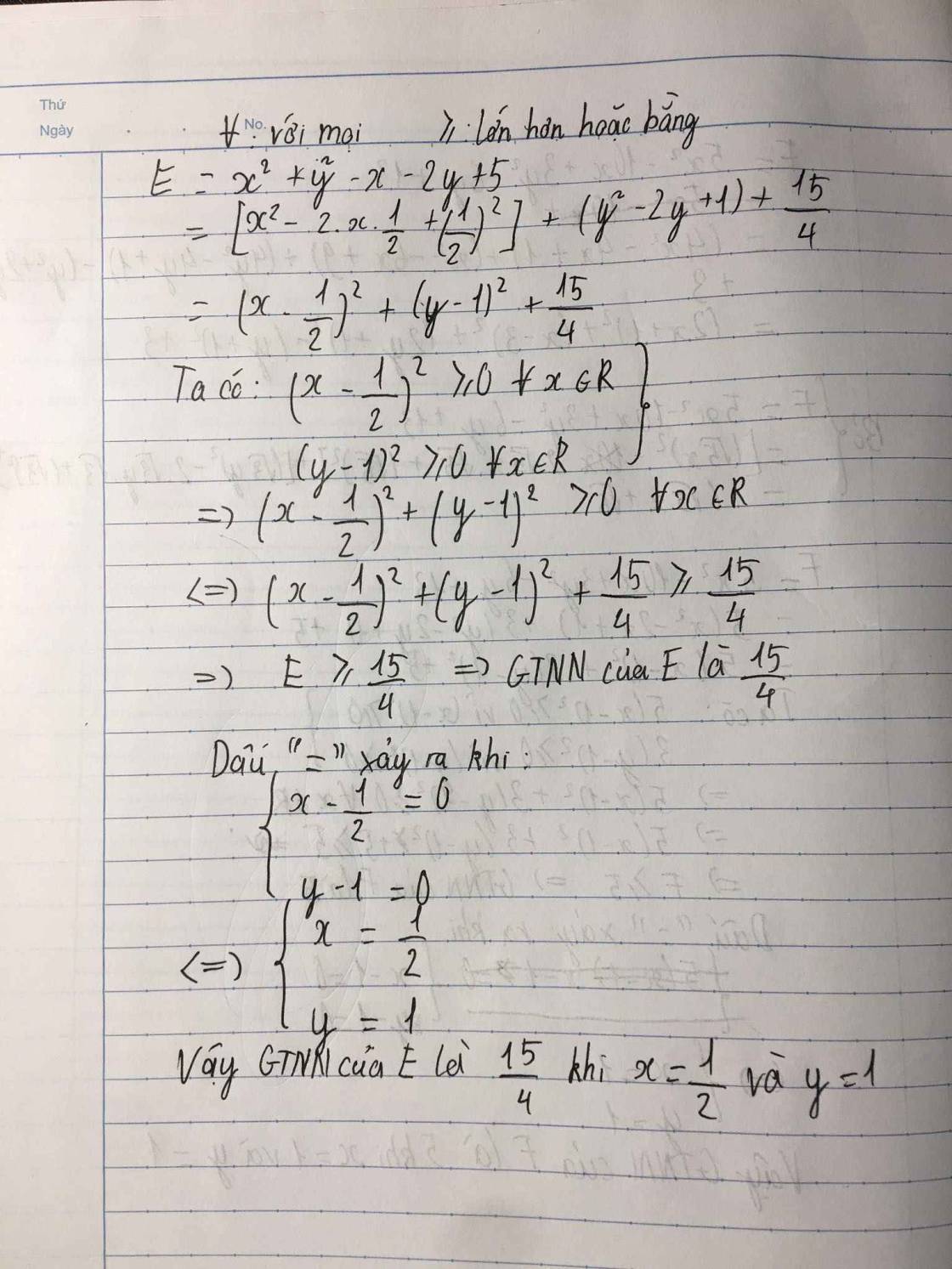2) Cho x+ 3y = 1. Tìm GTNN của Q= x2 + 3y2

Những câu hỏi liên quan
Cho x, y > 0 và x + y ≥1 . Tìm GTNN của P= (21x2 +1)/3y+(3y2+2)/4
1. cho x+y = 1 . tìm GTNN của biểu thức C = x2 + y2
2. cho x + 2y =1 . tìm GTNN của biểu thức P = x2 + 2y2
3. cho x + y =1 . tìm GTNN của biểu thức G = 2x2 + y2
4. cho x + y =1 . tìm GTNN của biểu thức H = x2 + 3y2
5. cho 2x + y =1 . tìm GTNN của biểu thức I = 4x2 + 2y2
6. tìm các số thực thõa mãn Pt :
2x2 + 5y2 + 8x - 10y + 13 = 0
Áp dụng Bunyakovsky, ta có :
\(\left(1+1\right)\left(x^2+y^2\right)\ge\left(x.1+y.1\right)^2=1\)
=> \(\left(x^2+y^2\right)\ge\frac{1}{2}\)
=> \(Min_C=\frac{1}{2}\Leftrightarrow x=y=\frac{1}{2}\)
Mấy cái kia tương tự
Đúng 1
Bình luận (0)
tìm GTNN của biểu thức
E=x2+y2-x-2y+5
F=5x2-10x+3y2-6y+13
Tìm GTNN của biểu thức M = x2 - 2x(y+1) + 3y2 + 2025
Ta có:
\(M=x^2-2x\left(y+1\right)+3y^2+2025\)
\(M=x^2-2\cdot x\cdot\left(y+1\right)+\left(y+1\right)^2+3y^2+2025-\left(y+1\right)^2\)
\(M=\left[x-\left(y+1\right)\right]^2+3y^2+2025-y^2-2y-1\)
\(M=\left(x-y-1\right)^2+2y^2-2y+2024\)
\(M=\left(x-y-1\right)^2+2\left(y-\dfrac{1}{2}\right)^2+\dfrac{4047}{2}\)
Mà: \(\left\{{}\begin{matrix}\left(x-y-1\right)^2\ge0\\2\left(y-\dfrac{1}{2}\right)^2\ge0\end{matrix}\right.\)
\(\Rightarrow M=\left(x-y-1\right)^2+2\left(y-\dfrac{1}{2}\right)^2+\dfrac{4047}{2}\ge\dfrac{4047}{2}\)
Dấu "=" xảy ra khi:
\(\left\{{}\begin{matrix}x-y-1=0\\y-\dfrac{1}{2}=0\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=\dfrac{1}{2}+1\\y=\dfrac{1}{2}\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=\dfrac{3}{2}\\y=\dfrac{1}{2}\end{matrix}\right.\)
Vậy GTNN của M là ....
Đúng 6
Bình luận (0)
(Nghỉ dịch từ ngày 28/2/2022)Bài 1:a) Cho hai đa thức: M 2x2 – 2xy – 3y2 + 1; N x2 – 2xy + 3y2 – 1Tính M + N; M – N.b) Cho hai đa thức: P(x) x3 – 6x + 2; Q(x) 2x2 - 4x3 + x - 5+ Tính P(x) + Q(x)+ Tính P(x) - Q(x)Bài 2: Tìm x biết:a) (x - 8 )( x3+ 8) 0; b) (4x - 3) – ( x + 5) 3(10 - x)Bài 3: Cho đa thức: P(x) 5x3 + 2x4 – x2 + 3x2 – x3 – 2x4 + 1 – 4x3.a) Thu gọn và xắp sếp các hạng tử của đa thức trên theo lũy thừa giảm của biến.b) Tính P(1) và P(–1).Bài 4: Tính nhanh...
Đọc tiếp
(Nghỉ dịch từ ngày 28/2/2022)
Bài 1:
a) Cho hai đa thức: M = 2x2 – 2xy – 3y2 + 1; N = x2 – 2xy + 3y2 – 1
Tính M + N; M – N.
b) Cho hai đa thức: P(x) = x3 – 6x + 2; Q(x) = 2x2 - 4x3 + x - 5
+ Tính P(x) + Q(x)
+ Tính P(x) - Q(x)
Bài 2: Tìm x biết:
a) (x - 8 )( x3+ 8) = 0; b) (4x - 3) – ( x + 5) = 3(10 - x)
Bài 3: Cho đa thức: P(x) = 5x3 + 2x4 – x2 + 3x2 – x3 – 2x4 + 1 – 4x3.
a) Thu gọn và xắp sếp các hạng tử của đa thức trên theo lũy thừa giảm của biến.
b) Tính P(1) và P(–1).
Bài 4: Tính nhanh (nếu có thể):
Bài 5: Cho tam giác ABC có AB = AC = 5cm, BC = 6cm. Đường trung tuyến AM xuất phát từ đỉnh A của tam giác ABC.
a) Chứng minh ΔAMB = ΔAMC và AM là tia phân giác của góc A.
b) Chứng minh AM vuông góc với BC.
c) Tính độ dài các đoạn thẳng BM và AM.
d) Từ M vẽ ME AB (E thuộc AB) và MF AC (F thuộc AC). Tam giác MEF là tam giác gì? Vì sao?
Bài 6: Cho ΔABC cân có AB = AC = 5cm, BC = 8cm. Kẻ AH vuông góc với BC.
a) Chứng minh: HB = HC.
b) Tính độ dài AH.
c) Kẻ HD vuông góc với AB (D∈AB), kẻ HE vuông góc với AC (E∈AC).
Chứng minh ΔHDE cân.
d) So sánh HD và HC.
Bài 2:
a: \(\left(x-8\right)\left(x^3+8\right)=0\)
=>\(\left[{}\begin{matrix}x-8=0\\x^3+8=0\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=8\\x^3=-8\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=8\\x=-2\end{matrix}\right.\)
b: \(\left(4x-3\right)-\left(x+5\right)=3\left(10-x\right)\)
=>\(4x-3-x-5=30-3x\)
=>3x-8=30-3x
=>6x=38
=>\(x=\dfrac{38}{6}=\dfrac{19}{3}\)
Bài 6:
a: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC
AH chung
Do đó: ΔAHB=ΔAHC
=>HB=HC
b: Ta có: HB=HC
H nằm giữa B và C
Do đó: H là trung điểm của BC
=>\(HB=HC=\dfrac{8}{2}=4\left(cm\right)\)
ΔAHB vuông tại H
=>\(AH^2+HB^2=AB^2\)
=>\(AH^2=5^2-4^2=9\)
=>\(AH=\sqrt{9}=3\left(cm\right)\)
c: Ta có: ΔAHB=ΔAHC
=>\(\widehat{BAH}=\widehat{CAH}\)
Xét ΔADH vuông tại D và ΔAEH vuông tại E có
AH chung
\(\widehat{DAH}=\widehat{EAH}\)
Do đó: ΔADH=ΔAEH
=>HD=HE
=>ΔHDE cân tại H
d: Ta có: HD=HE
HE<HC(ΔHEC vuông tại E)
Do đó:HD<HC
Đúng 0
Bình luận (0)
1, Cho x,yge0 thỏa mãn 2x+3y1 Tìm GTLN, GTNN của Ax^2+3y^22, Cho x^2+y^252 Tìm GTLN, GTNN của A2x+3y+43, Cho x,y0và x+y1 Tìm GTNN của Aleft(1+frac{1}{x}right)left(1+frac{1}{y}right)
Đọc tiếp
1, Cho \(x,y\ge0\) thỏa mãn \(2x+3y=1\) Tìm GTLN, GTNN của \(A=x^2+3y^2\)
2, Cho \(x^2+y^2=52\) Tìm GTLN, GTNN của \(A=2x+3y+4\)
3, Cho \(x,y>0\)và \(x+y=1\) Tìm GTNN của \(A=\left(1+\frac{1}{x}\right)\left(1+\frac{1}{y}\right)\)
1. Cho x,y thỏa mãn: x2 + 5y2 - 4xy + 2y = 3. Tìm x,y sao cho x đạt GTLN
2. Cho x,y thỏa mãn: 3x2 + y2 + 2xy + 4 = 7x + 3y
a) Tìm GTNN, GTLN của biểu thức P = x + y
b) Tìm GTNN, GTLN của x
3. Cho x,y thỏa mãn: x2 + 2y2 + 2xy + 7x + 7y + 10 = 0. Tìm GTLN, GTNN của S = x + y
tìm gtnn;
a, A= 3y2 cộng 6y cộng 5.
b, B= [x cộng 1].[x2 cộng 4x cộng 5].[x cộng 5]
a) Cho hai đa thức: M = 2x2 – 2xy – 3y2 + 1; N = x2 – 2xy + 3y2 – 1
Tính M + N; M – N.
b) Cho hai đa thức: P(x) = x3 – 6x + 2; Q(x) = 2x2 - 4x3 + x - 5
+ Tính P(x) + Q(x)
+ Tính P(x) - Q(x)
a, \(M+N=2x^2+x^2-2xy-2xy-3y^2+3y^2+1-1=3x^2-4xy\)
\(M-N=2x^2-x^2-2xy+2xy-3y^2-3y^2+1+1=x^2-6y^2+2\)
b, \(P\left(x\right)+Q\left(x\right)=x^3-4x^3+2x^2-6x+x+2-5=-3x^3+2x^2-5x-3\)
\(P\left(x\right)-Q\left(x\right)=x^3+4x^3-2x^2-6x-x+2+5=5x^3-2x^2-7x+7\)
Đúng 0
Bình luận (0)