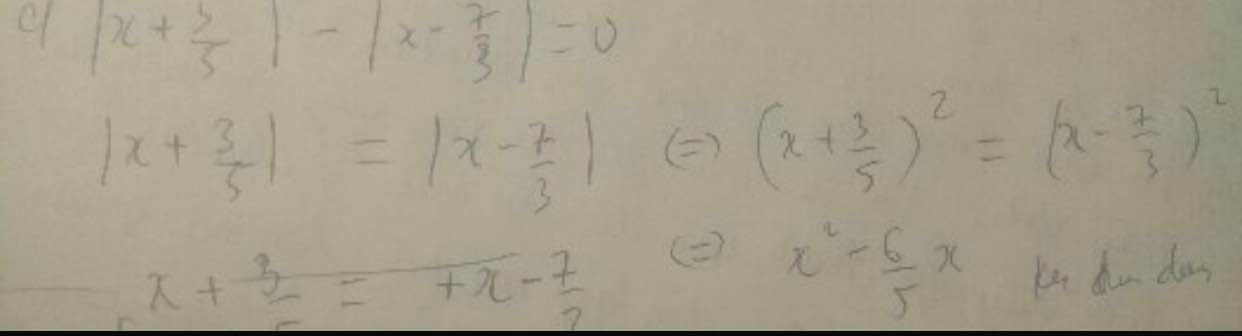Tìm x: \(\left(x-2\right)\left(x+\dfrac{3}{4}\right)>0\)

Những câu hỏi liên quan
Tìm x :
1) \(\left(-0,75x+\dfrac{5}{2}\right).\dfrac{4}{7}-\left(-\dfrac{1}{3}\right)=-\dfrac{5}{6}\)
2) \(\left(4x-9\right)\left(2,5+\dfrac{-7}{3}x\right)=0\)
3) \(\left|x-\dfrac{3}{4}\right|-\dfrac{1}{2}=0\)
4)\(\left(\dfrac{3}{5}-\dfrac{2}{3}x\right)^3=\dfrac{-64}{125}\)
3: \(\left|x-\dfrac{3}{4}\right|-\dfrac{1}{2}=0\)
\(\Leftrightarrow\left|x-\dfrac{3}{4}\right|=\dfrac{1}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}x-\dfrac{3}{4}=\dfrac{1}{2}\\x-\dfrac{3}{4}=-\dfrac{1}{2}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5}{4}\\x=\dfrac{1}{4}\end{matrix}\right.\)
Đúng 2
Bình luận (0)
Tìm x, biết : a/ dfrac{1}{3}xleft(x^2-4right)0b/ xleft(x+5right)x+5c/ x^3-dfrac{1}{9}x03)^2-left(x+5right)^20e/ left(x+2right)^2-left(x-2right)left(x+2right)0f/ xleft(2x-3right)-6+4x0g/ 2left(3x-2right)^2-9x^2+40h/ x^2left(x+1right)+2xleft(x+1right)0i/ 4x^2+9x+50
Đọc tiếp
Tìm x, biết :
a/ \(\dfrac{1}{3}x\left(x^2-4\right)=0\)
b/ \(x\left(x+5\right)=x+5\)
c/ \(x^3-\dfrac{1}{9}x=0\)
3)\(^2-\left(x+5\right)^2=0\)
e/ \(\left(x+2\right)^2-\left(x-2\right)\left(x+2\right)=0\)
f/ \(x\left(2x-3\right)-6+4x=0\)
g/ \(2\left(3x-2\right)^2-9x^2+4=0\)
h/ \(x^2\left(x+1\right)+2x\left(x+1\right)=0\)
i/ \(4x^2+9x+5=0\)
a) \(\Rightarrow\dfrac{1}{3}x\left(x-2\right)\left(x+2\right)=0\Rightarrow\left[{}\begin{matrix}x=0\\x=2\\x=-2\end{matrix}\right.\)
b) \(\Rightarrow\left(x+5\right)\left(x-1\right)=0\Rightarrow\left[{}\begin{matrix}x=-5\\x=1\end{matrix}\right.\)
c) \(\Rightarrow x\left(x^2-\dfrac{1}{9}\right)=0\Rightarrow x\left(x-\dfrac{1}{3}\right)\left(x+\dfrac{1}{3}\right)=0\Rightarrow\left[{}\begin{matrix}x=0\\x=\dfrac{1}{3}\\x=-\dfrac{1}{3}\end{matrix}\right.\)
e) \(\Rightarrow\left(x+2\right)\left(x+2-x+2\right)=0\Rightarrow\left(x+2\right).4=0\Rightarrow x=-2\)
f) \(\Rightarrow x\left(2x-3\right)+2\left(2x-3\right)=0\Rightarrow\left(2x-3\right)\left(x+2\right)=0\Rightarrow\left[{}\begin{matrix}x=\dfrac{3}{2}\\x=-2\end{matrix}\right.\)
g) \(\Rightarrow2\left(3x-2\right)^2-\left(3x-2\right)\left(3x+2\right)=0\Rightarrow\left(3x-2\right)\left(3x-6\right)=0\Rightarrow\left[{}\begin{matrix}x=\dfrac{2}{3}\\x=2\end{matrix}\right.\)
h) \(\Rightarrow x\left(x+1\right)\left(x+2\right)=0\Rightarrow\left[{}\begin{matrix}x=0\\x=-1\\x=-2\end{matrix}\right.\)
i) \(\Rightarrow4x\left(x+1\right)+5\left(x+1\right)=0\Rightarrow\left(x+1\right)\left(4x+5\right)=0\Rightarrow\left[{}\begin{matrix}x=-1\\x=-\dfrac{5}{4}\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Tìm x, biết:
a) \(\dfrac{-3}{2}x+\dfrac{1}{4}=\dfrac{1}{2}\left(x+1\right)\)
b) \(\left(6-3\sqrt{x}\right)\left(\left|x\right|-7\right)=0\)
a: \(-\dfrac{3}{2}x+\dfrac{1}{4}=\dfrac{1}{2}\left(x+1\right)\)
=>\(-\dfrac{3}{2}x+\dfrac{1}{4}=\dfrac{1}{2}x+\dfrac{1}{2}\)
=>\(-\dfrac{3}{2}x-\dfrac{1}{2}x=\dfrac{1}{2}-\dfrac{1}{4}\)
=>\(-2x=\dfrac{1}{4}\)
=>\(2x=-\dfrac{1}{4}\)
=>\(x=-\dfrac{1}{4}:2=-\dfrac{1}{8}\)
b: ĐKXĐ: x>=0
\(\left(6-3\sqrt{x}\right)\left(\left|x\right|-7\right)=0\)
=>\(\left\{{}\begin{matrix}6-3\sqrt{x}=0\\\left|x\right|-7=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}3\sqrt{x}=6\\\left|x\right|=7\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\sqrt{x}=2\\\left[{}\begin{matrix}x=7\left(nhận\right)\\x=-7\left(loại\right)\end{matrix}\right.\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=7\left(nhận\right)\\x=4\left(nhận\right)\end{matrix}\right.\)
Đúng 1
Bình luận (1)
Tìm x,biết
a)\(\left(x-2^2\right)-1=0\)
b)\(4-\left(x-2\right)^2=0\)
c)\(x^2-9-\dfrac{8}{9}x^2=0\)
d)\(\left(3x-2\right)^2-\left(2x+3\right)^2=5\left(x+4\right)\left(x-4\right)\)
a. (x - 22) - 1 = 0
<=> x - 4 - 1 = 0
<=> x = 5
b. 4 - (x - 2)2 = 0
<=> 22 - (x - 2)2 = 0
<=> (2 - x + 2)(2 + x - 2) = 0
<=> x(4 - x) = 0
<=> \(\left[{}\begin{matrix}x=0\\4-x=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=4\end{matrix}\right.\)
Đúng 2
Bình luận (2)
d. (3x - 2)2 - (2x + 3)2 = 5(x + 4)(x - 4)
<=> (3x - 2 - 2x - 3)(3x - 2 + 2x + 3) = 5(x2 - 16)
<=> (x - 5)(5x + 1) = 5x2 - 80
<=> 5x2 + x - 25x - 5 = 5x2 - 80
<=> 5x2 - 5x2 + x - 25x = -80 + 5
<=> -24x = -75
<=> x = \(\dfrac{25}{8}\)
Đúng 1
Bình luận (1)
a)\(\left(x-2^2\right)-1=0\Rightarrow x-4-1=0\Rightarrow x=5\)
Đúng 2
Bình luận (8)
Xem thêm câu trả lời
Tìm x ạ
b) \(\left|\dfrac{3}{4}x-\dfrac{3}{4}\right|-\dfrac{3}{4}=\left|\dfrac{-3}{4}\right|\)
c) \(\left|x+\dfrac{3}{5}\right|-\left|x-\dfrac{7}{3}\right|=0\)
Tìm GTNN của các hàm số sau:
a) \(f\left(x\right)=5+x+\dfrac{1}{x}\left(x>4\right)\)
b) \(g\left(x\right)=\left(x+2\right)\left(3+\dfrac{1}{x}\right)\left(x>0\right)\)
c) \(h\left(x\right)=\left(x+1\right)^2+\left(\dfrac{x^2}{x+1}+2\right)^2\left(x\ne-1\right)\)
c) \(h\left(x\right)=\left(x+1\right)^2+\left(\dfrac{x^2+2x+2}{x+1}\right)^2=\left(x+1\right)^2+\left(x+1+\dfrac{1}{x+1}\right)^2=2\left(x+1\right)^2+\dfrac{1}{\left(x+1\right)^2}+2\ge_{AM-GM}2\sqrt{2}+2\).
Đẳng thức xảy ra khi \(2\left(x+1\right)^2=\dfrac{1}{\left(x+1\right)^2}\Leftrightarrow x=\pm\sqrt{\dfrac{1}{2}}-1\).
Đúng 2
Bình luận (0)
b) \(g\left(x\right)=\dfrac{\left(x+2\right)\left(x+3\right)}{x}=\dfrac{x^2+5x+6}{x}=\left(x+\dfrac{6}{x}\right)+5\ge_{AM-GM}2\sqrt{6}+5\).
Đẳng thức xảy ra khi x = \(\sqrt{6}\).
Đúng 1
Bình luận (0)
Câu a muốn có min thì đề bài phải là \(x\ge4\) (có dấu "=")
Còn \(x>4\) thì chắc là đề sai
Đúng 2
Bình luận (0)
Tìm x biết:
\(a,\left(x-\dfrac{3}{4}\right)+50\%=\dfrac{1}{6}\)
\(b,\dfrac{1}{2}x-\dfrac{5}{6}x=\dfrac{7}{2}\)
\(c,\left(4-x\right)\left(3x+5\right)=0\)
\(d,\dfrac{x}{16}=\dfrac{50}{32}\)
\(e,\left(2x-3\right)+\dfrac{3}{2}=-\dfrac{1}{4}\)
a: =>x-3/4=1/6-1/2=1/6-3/6=-2/6=-1/3
=>x=-1/3+3/4=-4/12+9/12=5/12
b: =>x(1/2-5/6)=7/2
=>-1/3x=7/2
hay x=-21/2
c: (4-x)(3x+5)=0
=>4-x=0 hoặc 3x+5=0
=>x=4 hoặc x=-5/3
d: x/16=50/32
=>x/16=25/16
hay x=25
e: =>2x-3=-1/4-3/2=-1/4-6/4=-7/4
=>2x=-7/4+3=5/4
hay x=5/8
Đúng 0
Bình luận (0)
a) \(\left(x^2-16\right)\left(\dfrac{x}{4}-\dfrac{4x+5}{3}\right)=0\)
b) \(\left(4x-1\right)\left(x+5\right)=x^2-25\)
c) \(x\left(x+3\right)^3-\dfrac{x}{4}\left(x+3\right)=0\)
a) Ta có: \(\left(x^2-16\right)\left(\dfrac{x}{4}-\dfrac{4x+5}{3}\right)=0\)
\(\Leftrightarrow\left(x-4\right)\left(x+4\right)\left(\dfrac{3x-16x-20}{12}\right)=0\)
\(\Leftrightarrow\left(x-4\right)\left(x+4\right)\cdot\left(-13x-20\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-4=0\\x+4=0\\-13x-20=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=4\\x=-4\\-13x=20\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=4\\x=-4\\x=\dfrac{-20}{13}\end{matrix}\right.\)
Vậy: \(x\in\left\{4;-4;\dfrac{-20}{13}\right\}\)
b) Ta có: \(\left(4x-1\right)\left(x+5\right)=x^2-25\)
\(\Leftrightarrow\left(4x-1\right)\left(x+5\right)-\left(x^2-25\right)=0\)
\(\Leftrightarrow\left(4x-1\right)\left(x+5\right)-\left(x+5\right)\left(x-5\right)=0\)
\(\Leftrightarrow\left(x+5\right)\left(4x-1-x+5\right)=0\)
\(\Leftrightarrow\left(x+5\right)\left(3x+4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x+5=0\\3x+4=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-5\\3x=-4\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-5\\x=-\dfrac{4}{3}\end{matrix}\right.\)
Vậy: \(x\in\left\{-5;\dfrac{-4}{3}\right\}\)
c) Ta có: \(x\left(x+3\right)^3-\dfrac{x}{4}\cdot\left(x+3\right)=0\)
\(\Leftrightarrow\left(x+3\right)\cdot\left[x\left(x+3\right)^2-\dfrac{1}{4}x\right]=0\)
\(\Leftrightarrow\left(x+3\right)\left[x\left(x^2+6x+9\right)-\dfrac{1}{4}x\right]=0\)
\(\Leftrightarrow\left(x+3\right)\left(x^3+6x^2+9x-\dfrac{1}{4}x\right)=0\)
\(\Leftrightarrow\left(x+3\right)\cdot x\cdot\left(x^2+6x+\dfrac{35}{4}\right)=0\)
\(\Leftrightarrow x\left(x+3\right)\left(x^2+6x+9-\dfrac{1}{4}\right)=0\)
\(\Leftrightarrow x\left(x+3\right)\left[\left(x+3\right)^2-\dfrac{1}{4}\right]=0\)
\(\Leftrightarrow x\left(x+3\right)\left(x+3-\dfrac{1}{2}\right)\left(x+3+\dfrac{1}{2}\right)=0\)
\(\Leftrightarrow x\left(x+3\right)\left(x+\dfrac{5}{2}\right)\left(x+\dfrac{7}{2}\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x+3=0\\x+\dfrac{5}{2}=0\\x+\dfrac{7}{2}=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-3\\x=-\dfrac{5}{2}\\x=-\dfrac{7}{2}\end{matrix}\right.\)
Vậy: \(x\in\left\{0;-3;-\dfrac{5}{2};-\dfrac{7}{2}\right\}\)
Đúng 2
Bình luận (0)
1. Tìm GTNN của \(y=x+\dfrac{1}{x}-5\) trên \(\left(0,+\infty\right)\)
2. Tìm GTNN của \(y=4x^2+\dfrac{1}{x}-4\) trên \(\left(0,+\infty\right)\)
3. Tìm GTLN của \(y=\dfrac{x^2+4}{x}\) trên \(\left(-\infty,0\right)\)
\(y=x+\dfrac{1}{x}-5\ge2\sqrt{\dfrac{x}{x}}-5=-3\)
\(y_{min}=-3\) khi \(x=1\)
\(y=4x^2+\dfrac{1}{2x}+\dfrac{1}{2x}-4\ge3\sqrt[3]{\dfrac{4x^2}{2x.2x}}-4=-1\)
\(y_{min}=-1\) khi \(x=\dfrac{1}{2}\)
\(y=x+\dfrac{4}{x}\Rightarrow y'=1-\dfrac{4}{x^2}=0\Rightarrow x=-2\)
\(y\left(-2\right)=-4\Rightarrow\max\limits_{x>0}y=-4\) khi \(x=-2\)
Đúng 0
Bình luận (0)
Tìm x, biết
a, \(78x\left(x-97\right)-x+97=0\)
b, \(\dfrac{2}{3}x\left(x^2-4\right)=0\)
c, \(\left(x+2\right)^2-\left(x-2\right)\left(x+2\right)=0\)
giải chi tiết giúp mình
a: 78x(x-97)-x+97=0
=>(x-97)(78x-1)=0
=>\(\left[{}\begin{matrix}x=97\\x=\dfrac{1}{78}\end{matrix}\right.\)
b: \(\dfrac{2}{3}x\left(x^2-4\right)=0\)
=>\(x\left(x-2\right)\left(x+2\right)=0\)
=>\(\left[{}\begin{matrix}x=0\\x=2\\x=-2\end{matrix}\right.\)
c: \(\left(x+2\right)^2-\left(x-2\right)\left(x+2\right)=0\)
=>\(x^2+4x+4-x^2+4=0\)
=>4x+8=0
=>x+2=0
=>x=-2
Đúng 3
Bình luận (0)
\(a,78x\left(x-97\right)-x+97=0\)
\(\Leftrightarrow78x\left(x-97\right)-\left(x-97\right)=0\)
\(\Leftrightarrow\left(x-97\right)\left(78x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-97=0\\78x-1=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=97\\x=\dfrac{1}{78}\end{matrix}\right.\)
\(b,\dfrac{2}{3}x\left(x^2-4\right)=0\)
\(\Leftrightarrow\dfrac{2}{3}x\left(x-2\right)\left(x+2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}\dfrac{2}{3}x=0\\x-2=0\\x+2=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=2\\x=-2\end{matrix}\right.\)
\(c,\left(x+2\right)^2-\left(x-2\right)\left(x+2\right)=0\)
\(\Leftrightarrow\left(x+2\right)\left[\left(x+2\right)-\left(x-2\right)\right]=0\)
\(\Leftrightarrow\left(x+2\right)\left(x+2-x+2\right)=0\)
\(\Leftrightarrow\left(x+2\right)\cdot4=0\)
\(\Leftrightarrow x+2=0\)
\(\Leftrightarrow x=-2\)
Đúng 2
Bình luận (0)