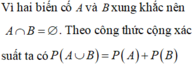Hãy tìm một biến cố khác rỗng và xung khắc với cả ba biến cố \(A,B\) và \(C\) trong Ví dụ 1.

Những câu hỏi liên quan
Tiếp tục với phép thử ở Ví dụ 1.
a) Gọi \(D\) là biến cố “Số chấm xuất hiện trên con xúc xắc thứ nhất là 3”. Hãy xác định các biến cố \(AD,BD\) và \(C{\rm{D}}\).
b) Gọi \(\bar A\) là biến cố đối của biến cố \(A\). Hãy viết tập hợp mô tả các biến cố giao \(\bar AB\) và \(\bar AC\).
a) \(D = \left\{ {\left( {3;1} \right);\left( {3;2} \right);\left( {3;3} \right);\left( {3;4} \right);\left( {3;5} \right);\left( {3;6} \right)} \right\}\)
\(A{\rm{D}} = \left\{ {\left( {3;2} \right)} \right\};B{\rm{D}} = \left\{ {\left( {3;2} \right)} \right\};C{\rm{D}} = \left\{ {\left( {3;1} \right)} \right\}\)
b) \(\bar AB = \left\{ {\left( {1;6} \right);\left( {6;1} \right)} \right\}\)
\(\bar A{\rm{C}} = \left\{ {\left( {1;6} \right);\left( {6;1} \right);\left( {1;5} \right);\left( {5;1} \right);\left( {1;3} \right);\left( {3;1} \right);\left( {1;2} \right);\left( {2;1} \right);\left( {1;1} \right)} \right\}\)
Đúng 0
Bình luận (0)
Hai xạ thủ cùng bắn vào bia. Kí hiệu
A
K
là biến cố: Người thứ K bắn trúng, k 1, 2.a. Hãy biểu diễn các biến cố sau qua các biến cố
A
1
,
A
2
;A: Không ai bắn trúngB: Cả hai đều bắn trúngC: Có đúng một người bắn trúngD: Có ít nhất một người bắn trúngb. Chứng tỏ rằng
A
D
; B và C xung khắc nh...
Đọc tiếp
Hai xạ thủ cùng bắn vào bia. Kí hiệu A K là biến cố: "Người thứ K bắn trúng", k = 1, 2.
a. Hãy biểu diễn các biến cố sau qua các biến cố A 1 , A 2 ;
A: "Không ai bắn trúng"
B: "Cả hai đều bắn trúng"
C: "Có đúng một người bắn trúng"
D: "Có ít nhất một người bắn trúng"
b. Chứng tỏ rằng A = D ; B và C xung khắc nhau.
Ak là biến cố: "Người thứ k bắn trúng"
- A1 : "Người thứ nhất bắn trúng"
⇒ 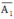 : “Người thứ nhất không bắn trúng”.
: “Người thứ nhất không bắn trúng”.
- A2 : "Người thứ hai bắn trúng"
⇒ 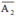 : “Người thứ hai không bắn trúng”.
: “Người thứ hai không bắn trúng”.

Đúng 0
Bình luận (0)
Cho hai biến cố xung khắc \(A\) và \(B\). Có 5 kết quả thuận lợi cho biến cố \(A\) và 12 kết quả thuận lợi cho biến cố \(B\). Hãy so sánh \(P\left( {A \cup B} \right)\) với \(P\left( A \right) + P\left( B \right)\).
Số kết quả thuận lợi cho biến cố \(A \cup B\) là \(5 + 12 = 17\).
\(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \frac{5}{{n\left( \Omega \right)}};P\left( B \right) = \frac{{n\left( B \right)}}{{n\left( \Omega\right)}} = \frac{{12}}{{n\left( \Omega\right)}};P\left( {A \cup B} \right) = \frac{{n\left( {A \cup B} \right)}}{{n\left( \Omega\right)}} = \frac{{17}}{{n\left( \Omega\right)}}\)
\( \Rightarrow P\left( A \right) + P\left( B \right) = P\left( {A \cup B} \right)\)
Đúng 0
Bình luận (0)
Cho hai biến cố A và B là hai biến cố xung khắc với P(A) > 0, P(B) > 0. Chứng tỏ rằng hai biến cố A và B không độc lập.
Hai biến cố A và B xung khắc khi và chỉ khi \(A \cap B = \emptyset \Rightarrow P\left( {AB} \right) = 0\)
Vì P(A) > 0, P(B) > 0 nên \(P\left( A \right).P\left( B \right) > 0\)
\( \Rightarrow P\left( {AB} \right) \ne P\left( A \right).P\left( B \right)\)
Vậy hai biến cố A và B không độc lập.
Đúng 0
Bình luận (0)
a) Hai biến cố đối nhau có xung khắc với nhau không?
b) Hai biến cố xung khắc có phải là hai biến cố đối nhau không?
a) Hai biến cố đối nhau không có xung khắc với nhau. Xung khắc xảy ra khi hai biến cố không thể xảy ra cùng một lúc.
b) Hai biến cố xung khắc không nhất thiết là hai biến cố đối nhau. Hai biến cố đối nhau xảy ra khi xảy ra một biến cố sẽ loại trừ hoàn toàn biến cố kia.
$HaNa$
Đúng 0
Bình luận (0)
Nếu hai biến cố A và B xung khắc thì xác suất của biến cố
P
A
∪
B
bằng A.
1
-
P
A
-
P
B
B.
P
A
.
P
B
-
P
A
-
P
B
C.
P
A...
Đọc tiếp
Nếu hai biến cố A và B xung khắc thì xác suất của biến cố P A ∪ B bằng
A. 1 - P A - P B
B. P A . P B - P A - P B
C. P A . P B
D. P A + P B
Nếu hai biến cố A và B xung khắc thì xác suất của biến cố P A ∪ B bằng
A. 1-P(A)-P(B)
B. P(A).P(B)
C. P(A).P(B)-P(A)-P(B)
D. P(A)+P(B)
Biến cố A và biến cố đối \(\overline A \) có xung khắc hay không? Tại sao?
Hai biến cố này có xung khắc vì \(\Omega=A\cup\overline{A}\)
Đúng 0
Bình luận (0)
Tung một đồng tiền đồng chất và cân đối ba lần. Kí hiệu Ak là biến cố.”lần giỏ thứ k xuất hiện mặt sấp”, với k=1,2,3. Hãy biểu diễn các biến cố sau qua các biến cố Ak và A không k A=“ cả 3 lần xuất hiện mặt sấp” B=“ cả 3 lần xuất hiện mặt ngửa” C=“ its nhất có một lần xuất hiện mặt sấp” D= “its nhất có 1 lần xuất hiện mặt ngửa”
Biến cố A: "Cả 3 lần xuất hiện mặt sấp"
=>\(A=\left\{A_1;A_2;A_3\right\}\)
Biến cố B: "Cả 3 lần xuất hiện mặt ngửa"
=>\(B=\left\{\overline{A_1};\overline{A_2};\overline{A_3}\right\}\)
Đúng 0
Bình luận (0)