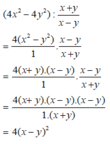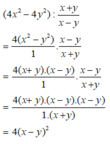4x2 + 8x + 4 - 4y2

Những câu hỏi liên quan
Viết biểu thức sau dưới dạng tổng của hai bình phương:
a. x2-2x+2+4y2+4y
b. 4x2+y2+12x+4y+13
c. x2+17+4y2+8x+4y
d. 4x2-12x+y2-4y+13
`a)x^2-2x+2+4y^2+4y`
`=x^2-2x+1+4y^2+4y+1`
`=(x-1)^2+(2y+1)^2`
`b)4x^2+y^2+12x+4y+13`
`=4x^2+12x+9+y^2+4y+4`
`=(2x+3)^2+(y+2)^2`
`c)x^2+17+4y^2+8x+4y`
`=x^2+8x+16+4y^2+4y+1`
`=(x+4)^2+(2y+1)^2`
`d)4x^2-12xy+y^2-4y+13`
`=4x^2-12x+9+y^2-4y+4`
`=(2x-3)^2+(y-2)^2`
Đúng 4
Bình luận (0)
a) \(x^2-2x+2+4y^2+4y=\left(x-1\right)^2+\left(2y+1\right)^2\)
b) \(4x^2+y^2+12x+4y+13=\left(2x+3\right)^2+\left(y+2\right)^2\)
c) \(x^2+17+4y^2+8x+4y=\left(x+4\right)^2+\left(2y+1\right)^2\)
d) \(4x^2-12x+y^2-4y+13=\left(2x-3\right)^2+\left(y-2\right)^2\)
Đúng 0
Bình luận (0)
a: \(x^2-2x+2+4y^2+4y\)
\(=x^2-2x+1+4y^2+4y+1\)
\(=\left(x-1\right)^2+\left(2y+1\right)^2\)
b: \(4x^2+12x+y^2+4y+13\)
\(=4x^2+12x+9+y^2+4y+4\)
\(=\left(2x+3\right)^2+\left(y+2\right)^2\)
c: \(x^2+8x+4y^2+4y+17\)
\(=x^2+8x+16+4y^2+4y+1\)
\(=\left(x+4\right)^2+\left(2y+1\right)^2\)
d: \(4x^2-12x+y^2-4y+13\)
\(=4x^2-12x+9+y^2-4y+4\)
\(=\left(2x-3\right)^2+\left(y-2\right)^2\)
Đúng 0
Bình luận (0)
4x2-8xy+4y2
\(4x^2-8xy+4y^2\\ =4\left(x^2-2xy+y^2\right)\\ =4\left(x-y\right)^2\)
Đúng 3
Bình luận (0)
`4x^2-8xy+4y^2`
`=4(x^2-2xy+y^2)`
`=4(x-y)^2`
Đúng 1
Bình luận (0)
a)4x2-4y2-20x+20y
b)16x2-25+(4x-5)
c)(x+5y)3
e)x2+4x+4-y2
g)x2-3x-4
\(a,4x^2-4y^2-20x+20y=4\left(x^2-y^2\right)-\left(20x-20y\right)=4\left(x-y\right)\left(x+y\right)-20\left(x-y\right)=\left(x-y\right)\left(4x+4y-20\right)=4\left(x-y\right)\left(x+y-5\right)\\ b,16x^2-25+\left(4x-5\right)=\left(4x-5\right)\left(4x+5\right)+\left(4x-5\right)=\left(4x-5\right)\left(4x+5+1\right)=\left(4x-5\right)\left(4x+6\right)=2\left(4x-5\right)\left(2x+3\right)\)
\(c,\left(x+5y\right)^3=x^3+15x^2y+75xy^2+125y^3\\ e,x^2-4x+4-y^2=\left(x-2\right)^2-y^2=\left(x-y-2\right)\left(x+y-2\right)\\ g,x^2-3x-4=\left(x^2-4x\right)+\left(x-4\right)=x\left(x-4\right)+\left(x-4\right)=\left(x+1\right)\left(x-4\right)\)
Đúng 1
Bình luận (0)
Bài 1: Phân tích đa thức thành nhân tử: a) 4y3 + 16y2 + 16y b) 8x2-48x+6xy-36y c) 8x2-48x-6xy+36y d) a2 –2ab+b2 –4 e) 4–x2 –4xy–4y2 f) 8a2 –16a+8ax–16x g) 16–4x2 +8xy–4y2 h) –4x2 –16xy–16y2 Bài 2: Tìm x, biết: a) x3 – 6x2 + 9x = 0 b) 5x(x–6)+3x–18=0 c) 5x(x – 6) – 18 + 3x = 0 d) 5x(x – 6) – 3x + 18 = 0 e) (2x – 3)2 = (5 – x)2 f) (2x + 1)2 = (3x – 2)2 g) 16(2x–3)=-25x2 (3–2x)
b: \(8x^2-48x+6xy-36y\)
\(=8x\left(x-6\right)+6y\left(x-6\right)\)
\(=2\left(x-6\right)\left(4x+3y\right)\)
d: \(a^2-2ab+b^2-4\)
\(=\left(a-b\right)^2-4\)
\(=\left(a-b-2\right)\left(a-b+2\right)\)
Đúng 0
Bình luận (0)
4x2-1
X(x+y)-6x-6y
X2-2xy+y2-z2
A2+2+2a+2ab+b2-ac-bc
9x2-1 phần 4
X2-2x-4y2-4y
9(x-y)2-4(x+y)2
(3x-2y)2-(2x-3y)2
9(x-y)2-4(x+y)2
\(4x^2-1=\left(2x-1\right)\left(2x+1\right)\)
\(x\left(x+y\right)-6x-6y=\left(x+y\right)\left(x-6\right)\)
\(x^2-2xy+y^2-z^2=\left(x-y-z\right)\left(x-y+z\right)\)
\(9x^2-\dfrac{1}{4}=\left(3x-\dfrac{1}{2}\right)\left(3x+\dfrac{1}{2}\right)\)
Đúng 0
Bình luận (0)
x3-4x2+8x-8
=(x3-4x2+8x-4)-4
giải tiếp hộ mik vs
\(x^3-4x^2+8x-8\)
\(=x^3-2x^2+4x-2x^2+4x-8\)
\(=\left(x^3-2x^2+4x\right)-\left(2x^2-4x+8\right)\)
\(=x\left(x^2-2x+4\right)-2\left(x^2-2x+4\right)\)
\(=\left(x^2-2x+4\right)\left(x-2\right)\)
Đúng 3
Bình luận (2)
Thực hiện phép tính:
4
x
2
-
4
y
2
:
x
+
y
x
-
y
.
A.
4
x
-
y
B.
4
x...
Đọc tiếp
Thực hiện phép tính: 4 x 2 - 4 y 2 : x + y x - y .
A. 4 x - y
B. 4 x x - y
C. 4 x + y 2
D. 4 x - y 2
Thực hiện phép tính:
4
x
2
-
4
y
2
:
x
+
y
x
-
y
.
A.
4
x
-
y
B.
4
x...
Đọc tiếp
Thực hiện phép tính: 4 x 2 - 4 y 2 : x + y x - y .
A. 4 x - y
B. 4 x x - y
C. 4 x + y 2
D. 4 x - y 2
Bài 2: Rút gọn biểu thức
A=(x-2)(x2+2x+4)-(128+x3)
B=(2x+3y)(4x2-6xy+9y2)-(3x-2y)(9x2+6xy+4y2)
\(A=x^3-8-128-x^3=-136\\ B=8x^3+27y^3-27x^3+8y^3=-19x^3+35y^3\)
Đúng 2
Bình luận (0)
\(A=\left(x-2\right)\left(x^2+2x+4\right)-\left(128+x^3\right)=x^3-8-128-x^3=-136\)
\(B=\left(2x+3y\right)\left(4x^2-6xy+9y^2\right)-\left(3x-2y\right)\left(9x^2+6xy+4y^2\right)=8x^3+27y^3-27x^3+8y^3=-19x^3+35y^3\)
Đúng 1
Bình luận (0)
\(A=x^3+2x^2+4x-2x^2-4x-8-128-x^3\)
\(A=-136\)
\(B=\left(2x+3y\right)\left(2x-3y\right)^2-\left(3x-2y\right)\left(3x+2y\right)^2\)
\(B=\left(2x+3y\right)\left(2x-3y\right)\left(2x-3y\right)-\left(3x-2y\right)\left(3x+2y\right)\left(3x+2y\right)\)
\(B=\left(4x^2-9y^2\right)\left(2x-3y\right)-\left(9x^2-4y^2\right)\left(3x+2y\right)\)
\(B=8x^3-12x^2y-18xy^2-27y^3-27x^3-18x^2y+12xy^2+8y^3\)
\(B=-19x^3-30x^2y-6xy^2-19y^3\)
\(B=-19\left(x^3-y^3\right)-6xy\left(5x+y\right)\)
Đúng 0
Bình luận (0)