16 lượt xem
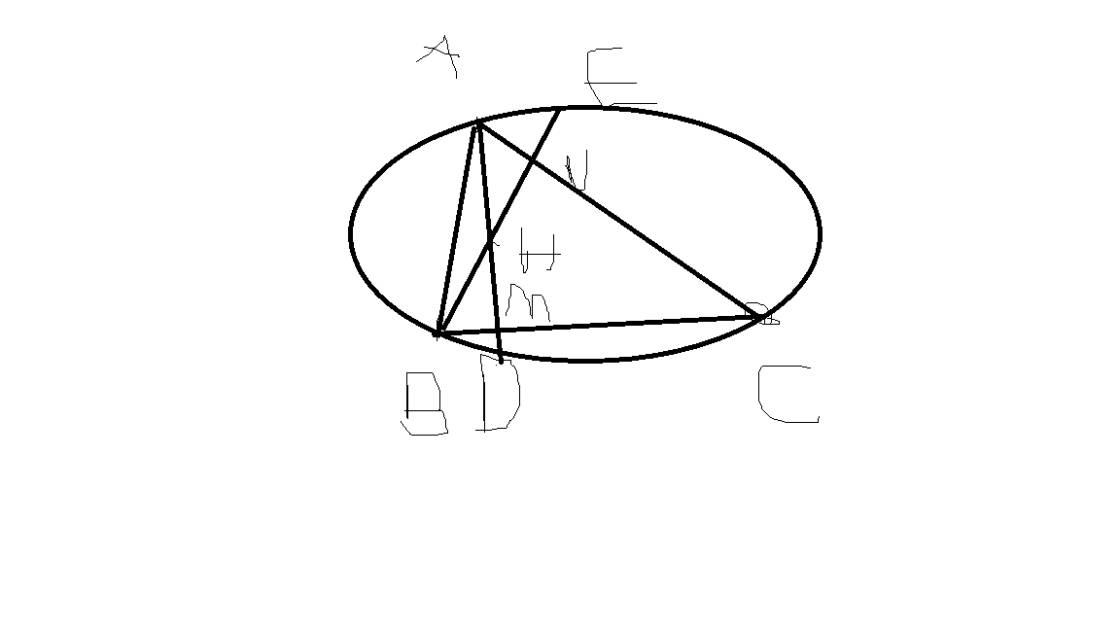
Cho tam giác nhọn ABC nội tiếp đường tròn (O;R). H là trực tâm của tam giác ABC. Từ B kẻ đường thẳng song song với HC. Từ C kẻ đường thẳng song song với HB. Hai đường thẳng này cắt nhau tại D. Hãy chứng minh:
1. Tứ giác ABDC nội tiếp và AD là đường kính của đường tròn (O;R)
2. BAH^ = CAO^
a. Gọi E là giao điểm của BC và HD; G là giao điểm của AE và OH. Chứng minh: G là trọng tâm của tam giác ABC.
b. Cho ABC ^= 60*. Tính diện tích hình quạt tròn COD (ứng với cung nhỏ CD).
4. Nếu OH song song với BC thì tanB.tanC = 3 với B, C là hai góc của tam giác ABC.