Tính giá trị của bthuc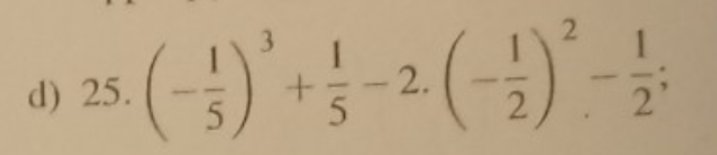

Những câu hỏi liên quan
Tính giá trị bthuc
b) \(\left[\left(\dfrac{1}{4}-0,5\right)\cdot2+\dfrac{8}{3}\right]:2\)
\(=\left[\left(\dfrac{1}{4}-\dfrac{1}{2}\right)\cdot2+\dfrac{8}{3}\right]:2\)
\(=\left[\left(\dfrac{1}{4}-\dfrac{2}{4}\right)\cdot2+\dfrac{8}{3}\right]:2\)
\(=\left(-\dfrac{1}{4}\cdot2+\dfrac{8}{3}\right):2\)
\(=\left(-\dfrac{1}{2}+\dfrac{8}{3}\right):2\)
\(=\dfrac{13}{6}:2\)
\(=\dfrac{13}{12}\)
d) \(\left(-0,75\right)-\left[\left(-2\right)+\dfrac{3}{2}\right]:1,5+\left(-\dfrac{5}{4}\right)\)
\(=\left(-0,75\right)-\left[\left(-2\right)+1,5\right]:1,5+\left(-\dfrac{5}{4}\right)\)
\(=\left(-0,75\right)-\left(-0,5\right):1,5+\left(-1,25\right)\)
\(=\left(-0,75\right)-\left(-\dfrac{1}{3}\right)-1,25\)
\(=-2+\dfrac{1}{3}\)
\(=-\dfrac{5}{3}\)
Đúng 1
Bình luận (0)
Tính giá trị bthuc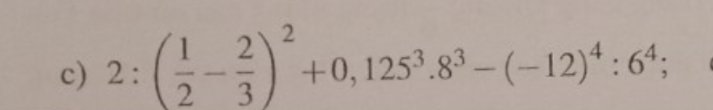
\(c,\)
\(2:\left(\dfrac{1}{2}-\dfrac{2}{3}\right)^2+0,125^3.8^3-\left(-12\right)^4:6^4\)
\(=2:\left(-\dfrac{1}{6}\right)^2+\left(\dfrac{1}{8}\right)^3.8^3-\left(-12\right)^4:6^4\)
\(=2:\dfrac{1}{36}+\left(\dfrac{1}{8}.8\right)^3-\left(-12:6\right)^4\)
\(=2.36+1^3-\left(-2\right)^4\)
\(=72+1-16\)
\(=57\)
Đúng 2
Bình luận (0)
Tìm giá trị nhỏ nhất của bthuc sau:
B= 2x^2 + 10x - 1
Tính giá trị lớn nhất của b.thức sau
C= 5x - x^2
\(B=2x^2+10x-1\)
=> \(B=2\left(x^2+5x\right)-1\)
=> \(B=2\left(x^2+2.x\frac{5}{2}+\frac{25}{4}\right)-\frac{27}{2}\)
=> \(B=2\left(x+\frac{5}{2}\right)^2-\frac{27}{2}\)
Có \(2\left(x+\frac{5}{2}\right)^2\ge0\)với mọi x
=> \(2\left(x+\frac{5}{2}\right)^2-\frac{27}{2}\ge\frac{-27}{2}\)
Dấu "=" xảy ra <=> \(\left(x+\frac{5}{2}\right)^2=0\)<=> \(x+\frac{5}{2}=0\)<=> \(x=\frac{-5}{2}\)
KL: Bmin = \(\frac{-27}{2}\)<=> \(x=\frac{-5}{2}\)
\(C=5x-x^2\)
=> \(C=-\left(x^2-5x\right)\)
=> \(C=-\left(x^2-2.x.\frac{5}{2}+\frac{25}{4}\right)+\frac{25}{4}\)
=> \(C=-\left(x-\frac{5}{2}\right)^2+\frac{25}{4}\)
Có \(\left(x-\frac{5}{2}\right)^2\ge0\)với mọi x
=> \(-\left(x-\frac{5}{2}\right)^2\le0\)
=> \(C=-\left(x-\frac{5}{2}\right)^2+\frac{25}{4}\le\frac{25}{4}\)
Dấu "=" xảy ra <=> \(\left(x-\frac{5}{2}\right)^2=0\)<=> \(x-\frac{5}{2}=0\)<=> \(x=\frac{5}{2}\)
KL: Cmax = \(\frac{25}{4}\)<=> \(x=\frac{5}{2}\)
Đúng 0
Bình luận (0)
B=2x2+10x-1=2(x2+5x-1/2)=2(x2+2*5/2*x+25/4-27/4)=2[x2+2*5/2*x+(5/2)2]-27/2=2(x+5/2)2-27/2
Ta có: (x+5/2)^2>=0(với mọi x)
=> 2(x+5/2)^2>=0(với mọi x)
=> 2(x+5/2)^2-27/2>=-27/2(với mọi x)
hay B>=-27/2( với mọi x)
Do đó, GTNN của B là -27/2 khi:
x+5/2=0
x=-5/2
Vậy GTNN của B là -27/2 khi x=-5/2
C=5x-x^2=-x^2+5x=-x^2+2*5/2*x-25/4+25/4=-[x^2-2*5/2*x+(5/2)^2]+25/4=-(x-5/2)^2+25/4
Ta có: (x-5/2)^2>=0(với mọi x)
=>-(x-5/2)^2<=0(với mọi x)
=> -(x-5/2)^2+25/4<=25/4(với mọi x) hay C<=25/4(với mọi x)
Do đó, GTLN của C là 25/4 khi: x-5/2=0
x=5/2
Vậy GTLN của C là 25/4 tại x=5/2
Đúng 0
Bình luận (0)
P= (6/x^2-9-5/3-x+1/x+3):2x-1/x^2-3x
a, Chứng minh P=6x/2x-1
b, Tính gt bthuc P khi P=1/3
c, Tìm những gt nguyên của x để bthuc P nhận giá trị nguyên
Tính giá trị bthuc
\(\sqrt{6-4\sqrt{ }2}+\sqrt{22-12\sqrt{ }2}\)
\(=\sqrt{\left(2-\sqrt{2}\right)^2}+\sqrt{\left(3\sqrt{2}-2\right)^2}\\ =2-\sqrt{2}+3\sqrt{2}-2=2\sqrt{2}\)
Đúng 2
Bình luận (0)
\(\sqrt{6-4\sqrt{2}}+\sqrt{22-12\sqrt{2}}\)
\(=\sqrt{\left(\sqrt{2}-2\right)^2}+\sqrt{\left(3\sqrt{2}-2\right)^2}\)
\(=2-\sqrt{2}+3\sqrt{2}-2=2\sqrt{2}\)
Đúng 1
Bình luận (0)
\(\sqrt{6-4\sqrt{2}}+\sqrt{22-12\sqrt{2}}\)
\(=2-\sqrt{2}+3\sqrt{2}-2\)
\(=2\sqrt{2}\)
Đúng 0
Bình luận (0)
Cho alpha là góc nhọn. Tính giá trị bthuc: M= cot alpha + tan alpha/cot alpha - tan alpha. Biết sin alpha = 3/5
sin a=3/5
=>cos a=4/5
tan a=3/5:4/5=3/4; cot a=1:3/4=4/3
M=(4/3+3/4):(4/3-3/4)=25/7
Đúng 0
Bình luận (0)
Tìm giá trị nhỏ nhất của bthuc sau:
B= 2x^2 + 10x - 1
\(B=2x^2+10x-1\)
\(\Rightarrow B=2\left(x^2+5x\right)-1\)
\(\Rightarrow B=2\left(x^2+2.x.\frac{5}{2}+\frac{25}{4}\right)-\frac{27}{2}\)
\(\Rightarrow B=\left(x+\frac{5}{2}\right)^2-\frac{27}{2}\)
Ta có : \(2\left(x+\frac{5}{2}\right)^2\ge0\)
\(\Rightarrow2\left(x+\frac{5}{2}\right)^2-\frac{27}{2}\ge\frac{-27}{2}\)
Dấu "=" xảy rak hi và chỉ khi \(\left(x+\frac{5}{2}\right)^2=0\)
\(\Leftrightarrow x+\frac{5}{2}=0\)
\(\Leftrightarrow x=-\frac{5}{2}\)
Vậy \(Min_B=\frac{-27}{2}\Leftrightarrow x=\frac{-5}{2}\)
Đúng 0
Bình luận (0)
tìm x sao cho giá trị của bthuc A = 2x - 7 luôn dương
tìm x sao cho giá trị của bth -3x không lớn hơn gtr của bth -7x + 5
Tính nhanh giá trị bthuc sau:
34 * 54 - (152 + 1)(152 - 1)
\(3^4.5^4-\left(15^2+1\right)\left(15^2-1\right)=15^4-\left(15^4-1\right)=15^4-15^4+1=1\)
Đúng 0
Bình luận (1)




















