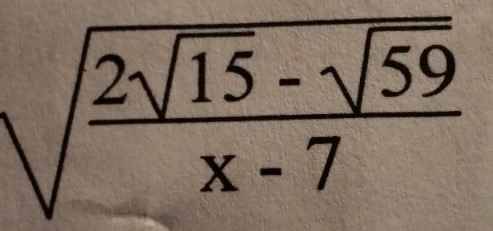
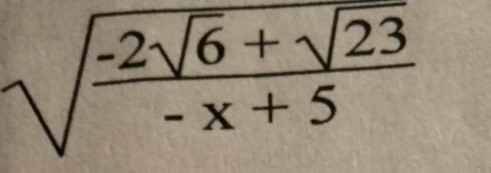
tìm đkxđ
tìm đkxđ √24+10
Vì các số trong căn bậc `2` không âm nên căn thức được xác định.
tìm đkxđ \(\sqrt{x}-1\)
2TH (mik dự đoán)
TH1: Nếu là \(\sqrt{x}-1\) => ĐKXĐ: x \(\ge\) 0
TH2: Nếu là \(\sqrt{x-1}\) => ĐKXĐ: \(x\ge1\)
tìm đkxđ \(\sqrt{x}+1\)
tìm đkxđ và rút gọn
ĐKXĐ: x<>0; x<>2; x<>1; x<>-1
\(Q=1+\dfrac{x+1+x+1-2x^2+2x-2}{\left(x+1\right)\left(x^2-x+1\right)}\cdot\dfrac{x\left(x^2-x-1\right)}{x^2\left(x-2\right)}\)
\(=1+\dfrac{-2x^2+4x}{\left(x+1\right)}\cdot\dfrac{1}{x\left(x-2\right)}\)
\(=1+\dfrac{-2x\left(x-2\right)}{x\left(x+1\right)\left(x-2\right)}=1+\dfrac{-2}{x+1}=\dfrac{x+1-2}{x+1}=\dfrac{x-1}{x+1}\)
tìm đkxđ \(\sqrt{9-x^2}\)
\(ĐKXĐ:9-x^2\ge0\Leftrightarrow x^2\le9\Leftrightarrow-3\le x\le3\)
tìm đkxđ \(\sqrt{4x^2-9}\)
\(ĐKXĐ:4x^2-9\ge0\\ \Leftrightarrow4x^2\ge9\\ \Leftrightarrow x^2\ge\dfrac{9}{4}\\ \Leftrightarrow\left\{{}\begin{matrix}x\ge\dfrac{3}{2}\\x\le-\dfrac{3}{2}\end{matrix}\right.\)
Tìm đkxđ: \(\dfrac{-5}{2x-5}\)
ĐKXĐ:
\(2x-5\ne0\Rightarrow x\ne\dfrac{5}{2}\)
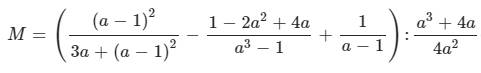
tìm đkxđ, tìm a để M>0 ( M= 4a/a^2+4 )
tìm đkxđ \(\sqrt{x^2-3x+7}\)
Đk: \(x^2-3x+7\ge0\)
\(\Leftrightarrow x^2-2.\dfrac{3}{2}x+\dfrac{9}{4}+\dfrac{19}{4}\ge0\)
\(\Leftrightarrow\left(x-\dfrac{3}{2}\right)^2+\dfrac{19}{4}\ge0\) (lđ với mọi x)
Vậy biểu thức luôn xác định với mọi x
\(\sqrt{x^2-3x+7}\)
Có \(x^2-3x+7=\left(x^2-3x+\dfrac{9}{4}\right)+\dfrac{19}{4}=\left(x-\dfrac{3}{2}\right)^2+\dfrac{19}{4}>0\forall x\)
ĐKXĐ: \(x\in R\)