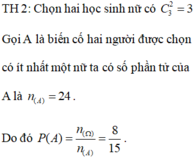Một lớp có 10 học sinh nam và 15 học sinh nữ. Chọn ngẫu nhiên 5 học sinh. Tính xác suất trong các trường hợp: a) có ít nhất 2 nam trong số được chọn. b) có ít nhất một sinh viên năm được chọn c) chọn được số năm nhiều hơn số nữ

Những câu hỏi liên quan
Chọn ngẫu nhiên 5 học sinh trong một lớp học gồm 25 nam và 20 nữ. Gọi A là biến cố “Trong 5 học sinh được chọn có ít nhất 1 học sinh nữ”. Xác suất của biến cố A là: A.
P
A
C
20
5
C
45
5
B.
P
A
20
.
C...
Đọc tiếp
Chọn ngẫu nhiên 5 học sinh trong một lớp học gồm 25 nam và 20 nữ. Gọi A là biến cố “Trong 5 học sinh được chọn có ít nhất 1 học sinh nữ”. Xác suất của biến cố A là:
A. P A = C 20 5 C 45 5
B. P A = 20 . C 25 4 C 45 5
C. P A = 20 . C 44 4 C 45 5
D. P A = 1 - C 25 5 C 45 5
Một nhóm gồm 10 học sinh trong đó có 7 học sinh nam và 3 học sinh nữ. Chọn ngẫu nhiên 3 học sinh từ nhóm 10 học sinh đó đi lao động. Tính xác suất để trong 3 học sinh được chọn có ít nhất một học sinh nữ A.
2
3
B.
17
48
C.
17
24
D.
4
9
Đọc tiếp
Một nhóm gồm 10 học sinh trong đó có 7 học sinh nam và 3 học sinh nữ. Chọn ngẫu nhiên 3 học sinh từ nhóm 10 học sinh đó đi lao động. Tính xác suất để trong 3 học sinh được chọn có ít nhất một học sinh nữ
A. 2 3
B. 17 48
C. 17 24
D. 4 9
Một nhóm gồm 10 học sinh trong đó có 7 học sinh nam và 3 học sinh nữ. Chọn ngẫu nhiên 3 học sinh từ nhóm 10 học sinh đó đi lao động. Tính xác suất để trong 3 học sinh được chọn có ít nhất một học sinh nữ. A.
2
3
. B.
17
48
. C.
17
24
. D.
4
9
.
Đọc tiếp
Một nhóm gồm 10 học sinh trong đó có 7 học sinh nam và 3 học sinh nữ. Chọn ngẫu nhiên 3 học sinh từ nhóm 10 học sinh đó đi lao động. Tính xác suất để trong 3 học sinh được chọn có ít nhất một học sinh nữ.
A. 2 3 .
B. 17 48 .
C. 17 24 .
D. 4 9 .
Đáp án C.
Phương pháp giải: Áp dụng các quy tắc đếm cơ bản
Lời giải:
Chọn 3 học sinh trong 10 học sinh có C 10 3 cách => n ( Ω ) = C 10 3 = 120 .
Gọi X là biến cố trong 3 học sinh được chọn có ít nhất một học sinh nữ
Ta xét các trường hợp sau:
TH1. Chọn 1 học sinh nữ và 2 học sinh nam => có C 7 2 . C 3 1 = 63 cách.
TH2. Chọn 2 học sinh nữ và 1 học sinh nam => có C 7 1 . C 3 2 = 21 cách.
TH3. Chọn 3 học sinh nữ và 0 học sinh nam => có C 3 3 = 1 cách.
Suy ra số kết quả thuận lợi cho biến cố X là n(X) = 63 + 21 + 1 = 85.
Vậy xác suất cần tính là P = n ( X ) n ( Ω ) = 85 120 = 17 24 .
Đúng 0
Bình luận (0)
Một nhóm gồm 10 học sinh trong đó có 7 học sinh nam và 3 học sinh nữ. Chọn ngẫu nhiên 3 học sinh từ nhóm 10 học sinh đi tham gia chương trình áo ấm vùng cao. Tính xác suất để 3 học sinh được chọn có ít nhất một học sinh nữ.
`n(\Omega)=C_10 ^3`
Gọi `\overline A:"` Chọn `3` h/s mà trong đó không có h/s nữ`."`
`=>n(\overline A)=C_7 ^3`
`=>P(A)=1-[C_7 ^3]/[C_10 ^3]=17/24`
Đúng 2
Bình luận (0)
Lớp 3A có 15 học sinh nam và 30 học sinh nữ.
a) Hỏi có bao nhiêu cách chọn một nhóm 5 học sinh sao cho vừa có nam vừa có nữ.
b) Chọn ngẫu nhiên 4 học sinh. Tính xác suất sao cho chọn được số nam nhiều hơn nữ.
c) Giả sử Lan là 1 trong 30 nữ. Chọn ngẫu nhiên 3 học sinh. Biết rằng Lan được chọn. Tính xác suất chọn được 3 nữ.
Một tổ trong lớp 10B có 12 học sinh, trong đó có 7 học sinh nam và 5 học sinh nữ. Giáo viên chọn ngẫu nhiên 6 học sinh trong tổ để kiểm tra vở bài tập Toán. Tính xác suất để trong 6 học sinh được chọn số học sinh nữ bằng số học sinh nam.
\(\Omega \) là tập tất cả 6 học sinh trong 12 học sinh. Vậy \(n\left( \Omega \right) = C_{12}^6 = 924\).
Gọi C là biến cố: “Có 3 học sinh nam và 3 học sinh nữ”. Có \(C_7^3\) cách chọn chọn 3 học sinh nam và \(C_5^3\) cách chọn 3 học sinh nữ. Theo quy tắc nhân, ta có \(C_7^3.C_5^3 = 350\) cách chọn 3 học sinh nam và 3 học sinh nữ tức là \(n\left( C \right) = 350\).Vậy \(P\left( C \right) = \frac{{350}}{{924}} \approx 0,3788\).
Đúng 0
Bình luận (0)
Một tổ học sinh có 7 nam và 3 nữ. Chọn ngẫu nhiên 2 người. Tính xác suất sao cho 2 người được chọn có ít nhất một nữ A.
1
15
B.
8
15
C.
7
15
D.
1
15
Đọc tiếp
Một tổ học sinh có 7 nam và 3 nữ. Chọn ngẫu nhiên 2 người. Tính xác suất sao cho 2 người được chọn có ít nhất một nữ
A. 1 15
B. 8 15
C. 7 15
D. 1 15
Một tổ học sinh có 7 nam và 3 nữ. Chọn ngẫu nhiên 2 người. Tính xác suất sao cho 2 người được chọn có ít nhất một nữ. A.
1
15
B.
8
15
C.
7
15
D.
1
5
Đọc tiếp
Một tổ học sinh có 7 nam và 3 nữ. Chọn ngẫu nhiên 2 người. Tính xác suất sao cho 2 người được chọn có ít nhất một nữ.
A. 1 15
B. 8 15
C. 7 15
D. 1 5
Lớp 7 A có 15 học sinh nữ và 25 học sinh nam. Chọn ra ngẫu nhiên một học sinh trong lớp. Tìm số phần tử của tập hợp E gồm các kết quả có thể xảy ra đối với học sinh được chọn ra. Sau đó, hãy tính xác suất của mỗi biến cố sau: a) “Học sinh được chọn ra là học sinh nữ”; b) “Học sinh được chọn ra là học sinh nam”;
a: n(E)=40
A là biến cố "học sinh được chọn ra là nữ"
n(A)=15
=>P(A)=15/40=3/8
b: biến cố học sinh được chọn ra là nam là biến cố đối của biến cố học sinh được chọn ra là nữ
=>P=1-3/8=5/8
Đúng 1
Bình luận (0)