giải giùm câu c d

Những câu hỏi liên quan
ai giải giùm mình bài toán 68/sgk lớp 7 câu c và câu d với
Ghi câu hỏi ra đi bn Nếu có thể mk sẽ giúp
Đúng 0
Bình luận (0)
giúp em giải giùm câu 5 d nha vẽ hình giùm ạ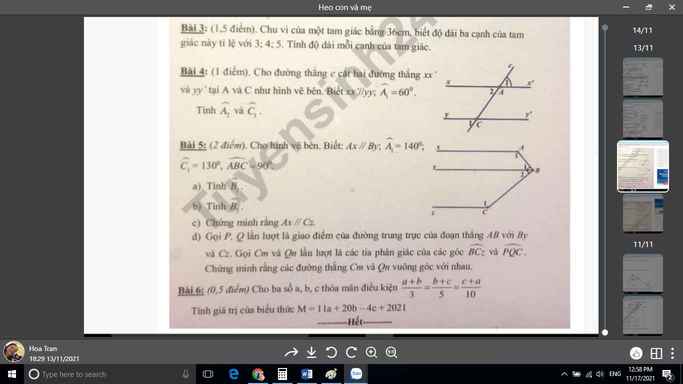
Câu 1. Tìm a,b,c,d thuộc Z biết:
|a-b| + |b-c| + |c-d| + |d-a| = 2019
Giải nhanh giùm mình!

giải giùm mik câu a và câu d đi
a) \(x^2-15=\left(x-\sqrt{15}\right)\left(x+\sqrt{15}\right)\)
d) \(x-6\sqrt{x}+9-\left(\sqrt{x}-1\right)^2=\left(\sqrt{x}-3\right)^2-\left(\sqrt{x}-1\right)^2=\left(\sqrt{x}-3-\sqrt{x}+1\right)\left(\sqrt{x}-3+\sqrt{x}-1\right)=-2\left(2\sqrt{x}-4\right)=-4\left(\sqrt{x}-2\right)\)
Đúng 2
Bình luận (2)
Giải giùm em câu d b1. b3 ý 2 câu b và b4 vs ạ
1:
d: P=A+B
\(=\dfrac{2\sqrt{x}}{\sqrt{x}+3}+\dfrac{15-\sqrt{x}+2\sqrt{x}-10}{x-25}\cdot\dfrac{\sqrt{x}-5}{\sqrt{x}+3}\)
\(=\dfrac{2\sqrt{x}}{\sqrt{x}+3}+\dfrac{1}{\sqrt{x}+3}=\dfrac{2\sqrt{x}+1}{\sqrt{x}+3}\)
P nguyên
=>2căn x+6-5 chia hết cho căn x+3
=>căn x+3 thuộc Ư(-5)
=>căn x+3=5
=>x=4
3:
2:
b: PTHĐGĐ là:
x^2-2(m+1)x+2m+1=0
Theo đề, ta có:
x1^2+x2^2=(căn 5)^2=5
=>(x1+x2)^2-2x1x2=5
=>(2m+2)^2-2(2m+1)=5
=>4m^2+8m+4-4m-2-5=0
=>4m^2+4m+1=0
=>m=-1/2
Đúng 0
Bình luận (0)

GIẢI giùm mik Câu C vs
Lời giải:
c. Đặt $\sqrt{x}=a; \sqrt{y}=b$ thì:
$C=a^3-b^3+a^2b-ab^2=(a-b)(a^2+ab+b^2)+ab(a-b)$
$=(a-b)(a^2+ab+b^2+ab)=(a-b)(a^2+2ab+b^2)$
$=(a-b)(a+b)^2=(\sqrt{x}-\sqrt{y})(\sqrt{x}+\sqrt{y})^2$
Đúng 1
Bình luận (0)
Cho tam giác ABC cân tại A. Gọi H là hình chiếu của A trên cạnh BC
a/C.m: tam giác ABH= tam giác ACH
b/Tính AH khi AB =10cm, BH=6cm
c/Gọi I là trung điểm của AC. BI cắt AH tại G. Chứng minh: AG=2GH
d/C.m: IH>IG.
giải giùm mình gấp nha! câu a,b,c khỏi giải câu d thì mình quên cách giải rồi, giúp giùm mình nha!
mọi người giải giùm mình bài 1 câu c
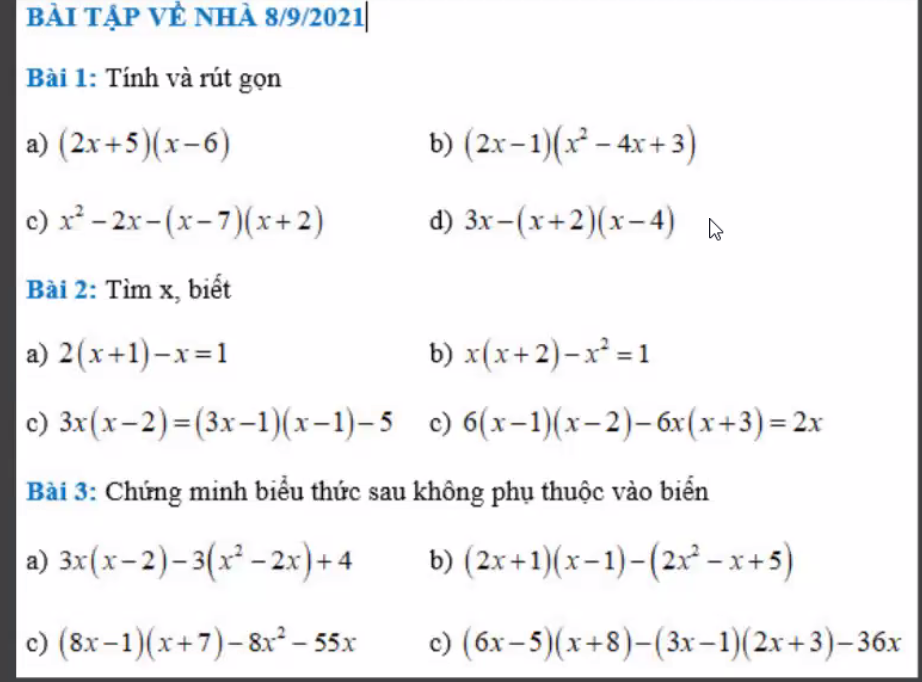
$x^2-2x-(x-7)(x+2)\\=x^2-2x-x^2+5x+14\\=3x+14$
Đúng 1
Bình luận (1)
Bài 1:
a. $(2x+5)(x-6)=2x^2-12x+5x-30$
$=2x^2-7x-30$
b. $(2x-1)(x^2-4x+3)=2x^3-8x^2+6x-x^2+4x-3$
$=2x^3-9x^2+10x-3$
c.
$x^2-2x-(x-7)(x+2)=x^2-2x-(x^2-5x-14)$
$=x^2-2x-x^2+5x+14=3x+14$
d.
$3x-(x+2)(x-4)=3x-(x^2-2x-8)$
$=3x-x^2+2x+8=-x^2+5x+8$
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
ai giải giùm e chi tiết câu c vs ạ

`a)A` có nghĩa `<=>x-1 >= 0 <=>x >= 1`
`b)B=\sqrt{3^2 .2}+\sqrt{2^3}-\sqrt{5^2 .2}`
`<=>B=3\sqrt{2}+2\sqrt{2}-5\sqrt{2}`
`<=>B=0`
`c)` Với `a >= 0,a \ne 1` có:
`C=[a-1]/[\sqrt{a}-1]-[a\sqrt{a}-1]/[a-1]`
`C=[(a-1)(\sqrt{a}+1)-a\sqrt{a}+1]/[(\sqrt{a}-1)(\sqrt{a}+1)]`
`C=[a\sqrt{a}+a-\sqrt{a}-1-a\sqrt{a}+1]/[(\sqrt{a}-1)(\sqrt{a}+1)]`
`C=a/[a-1]`
Đúng 3
Bình luận (0)























