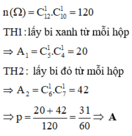Có hai túi đựng bi: túi số 1 có 3 bi đỏ, 2 bi xanh và túi số 2 có 4 bi đổ, 5 bi xanh. Từ mỗi túi lấy ngẫu nhiên ra 1 bi. Tính xác suất để lấy ra 2 bi cùng màu

Những câu hỏi liên quan
Có hai túi đựng các viên bị có cùng kích thước và khối lượng. Túi I có 3 viên bi màu xanh và 7 viên bị màu đỏ. Túi II có 10 viên bi màu xanh và 6 viên bi màu đỏ. Từ mỗi túi, lấy ngẫu nhiên ra một viên bị. Tính xác suất để:a) Hai viên bi được lấy có cùng màu xanh;b) Hai viên bi được lấy có cùng màu đỏ;c) Hai viên bi được lấy có cùng màu;d) Hai viên bi được lấy không cùng màu.
Đọc tiếp
Có hai túi đựng các viên bị có cùng kích thước và khối lượng. Túi I có 3 viên bi màu xanh và 7 viên bị màu đỏ. Túi II có 10 viên bi màu xanh và 6 viên bi màu đỏ. Từ mỗi túi, lấy ngẫu nhiên ra một viên bị. Tính xác suất để:
a) Hai viên bi được lấy có cùng màu xanh;
b) Hai viên bi được lấy có cùng màu đỏ;
c) Hai viên bi được lấy có cùng màu;
d) Hai viên bi được lấy không cùng màu.
Vì hai túi là khác nhau nên biến cố lấy một viên bi mỗi túi là độc lập.
Gọi biến cố A: “Hai viên bi được lấy có cùng màu xanh”, biến cố B: “Hai viên bi được lấy có cùng màu đỏ”, biến cố C: “Hai viên bi được lấy có cùng màu”
a) Xác suất lấy được viên bi màu xanh từ túi I là \(\frac{3}{{10}}\)
Xác suất lấy được viên bi màu xanh từ túi II là \(\frac{{10}}{{16}} = \frac{5}{8}\)
Xác suất lấy được hai viên bi cùng màu xanh là \(\frac{3}{{10}}.\frac{5}{8} = \frac{3}{{16}}\)
b) Xác suất lấy được viên bi màu đỏ từ túi I là \(\frac{7}{{10}}\)
Xác suất lấy được viên bi màu đỏ từ túi II là \(\frac{6}{{16}} = \frac{3}{8}\)
Xác suất lấy được hai viên bi cùng màu đỏ là \(\frac{7}{{10}}.\frac{3}{8} = \frac{{21}}{{80}}\)
c) Ta có \(C = A \cup B\) mà A và B xung khắc nên
\(P\left( C \right) = P\left( {A \cup B} \right) = P\left( A \right) + P\left( B \right) = \frac{3}{{16}} + \frac{{21}}{{80}} = \frac{9}{{20}}\)
Vậy xác suất để hai viên bi được lấy có cùng màu là \(\frac{9}{{20}}.\)
d) Gọi biến cố D: “Hai viên bi được lấy không cùng màu”
Khi đó \(\overline D = C\)
\( \Rightarrow P\left( D \right) = 1 - P\left( {\overline D } \right) = 1 - P\left( C \right) = 1 - \frac{9}{{20}} = \frac{{11}}{{20}}\)
Vậy xác suất để hai viên bi được lấy không cùng màu là \(\frac{{11}}{{20}}.\)
Đúng 1
Bình luận (0)
Một túi đựng 1 viên bi xanh, 1 viên bi đỏ, 1 viên bi trắng và 1 viên bi vàng có cùng kích thước và khối lượng. Lấy ngẫu nhiên 2 viên bi từ túi. Tính xác suất của các biến cố:
\(A\): “Trong hai viên bi lấy ra có 1 viên bi màu đỏ”;
\(B\): “Hai viên bi lấy ra đều không có màu trắng”.
a) Cách lấy 2 viên bi trong túi là:
Xanh – đỏ; Xanh – trắng; Xanh – vàng; Đỏ - trắng; Đỏ - vàng; Trắng – vàng.
Có 6 cách lấy hai biên bi từ trong túi.
Biến cố \(A\) xảy ra khi 2 viên bi lấy ra có 1 viên bi màu đỏ
Có 3 kết quả thuận lợi cho biến cố \(A\) là Xanh – đỏ; Đỏ - trắng; Đỏ - vàng
Xác suất 2 viên bi lấy ra có 1 viên bi màu đỏ là \(\frac{3}{6} = \frac{1}{2}\).
Vậy xác suất 2 viên bi lấy ra có 1 viên bi màu đỏ là \(\frac{1}{2}\).
b) Biến cố \(B\) xảy ra khi 2 viên bi lấy ra đều không có màu trắng
Có 3 kết quả thuận lợi cho \(B\) là : Xanh – đỏ; Xanh – vàng; Đỏ - vàng.
Xác suất 2 viên bi lấy ra không có viên bi nào màu trắng là \(\frac{3}{6} = \frac{1}{2}\).
Vậy xác suất 2 viên bi lấy ra không có viên bi nào màu trắng là \(\frac{1}{2}\).
Đúng 0
Bình luận (0)
Có hai chiếc túi, chiếc túi đầu tiên đựng 4 viên bi màu xanh và 3 viên bi màu vàng, chiếc túi còn lại chứa 3 viên bi màu xanh và 5 viên bi màu vàng. Chọn ngẫu nhiên một viên bi.a) Tính xác suất để lấy ra được một viên bi xanhb) Nếu một viên bi xanh được lấy ra, tính xác suất mà nó được lấy ra từ chiếc túi thứ nhất.
Đọc tiếp
Có hai chiếc túi, chiếc túi đầu tiên đựng 4 viên bi màu xanh và 3 viên bi màu vàng, chiếc túi còn lại chứa 3 viên bi màu xanh và 5 viên bi màu vàng. Chọn ngẫu nhiên một viên bi.
a) Tính xác suất để lấy ra được một viên bi xanh
b) Nếu một viên bi xanh được lấy ra, tính xác suất mà nó được lấy ra từ chiếc túi thứ nhất.
a: n(omega)=4+3+3+5=15
n(xanh)=4+3=7
=>P=7/15
b: P=7/15*4/7=4/15
Đúng 0
Bình luận (0)
Có hai hộp đựng bi. Hộp thứ nhất đựng 7 bi đỏ và 5 bi xanh. Hộp thứ hai đựng 6 bi đỏ và 4 bi xanh. Từ mỗi hộp lấy ngẫu nhiên một bi, tính xác suất để 2 bi được lấy ra có cùng màu. A.
31
60
B.
41
60
C.
51
60
D.
11
60
Đọc tiếp
Có hai hộp đựng bi. Hộp thứ nhất đựng 7 bi đỏ và 5 bi xanh. Hộp thứ hai đựng 6 bi đỏ và 4 bi xanh. Từ mỗi hộp lấy ngẫu nhiên một bi, tính xác suất để 2 bi được lấy ra có cùng màu.
A. 31 60
B. 41 60
C. 51 60
D. 11 60
Có hai hộp đựng bi. Hộp thứ nhất đựng 7 bi đỏ và 5 bi xanh. Hộp thứ hai đựng 6 bi đỏ và 4 bi xanh. Từ mỗi hộp lấy ngẫu nhiên một bi, tính xác suất để 2 bi được lấy ra có cùng màu. A.
31
60
B.
41
60
C.
51
60
D.
11
60
Đọc tiếp
Có hai hộp đựng bi. Hộp thứ nhất đựng 7 bi đỏ và 5 bi xanh. Hộp thứ hai đựng 6 bi đỏ và 4 bi xanh. Từ mỗi hộp lấy ngẫu nhiên một bi, tính xác suất để 2 bi được lấy ra có cùng màu.
A. 31 60
B. 41 60
C. 51 60
D. 11 60
cho hai chiếc túi kín l, ll đựng một số viên bi có cùng kích thước, trong đó tất cả các viên bi ở túi l có màu đen. Ngườ chơi lấy ngẫu nhiên từ mỗi túi một viên bi và sẽ thắng cuộc nếu trong hai viên bi lấy ra có viên bi màu đỏ. Trong túi ll cần có những viên bi có màu gì để biến cố Người chơi thắng là:a) Biến cố chắc chắn;b) Biến cố không thể;c) Biến cố ngẫu nhiên?
Đọc tiếp
cho hai chiếc túi kín l, ll đựng một số viên bi có cùng kích thước, trong đó tất cả các viên bi ở túi l có màu đen. Ngườ chơi lấy ngẫu nhiên từ mỗi túi một viên bi và sẽ thắng cuộc nếu trong hai viên bi lấy ra có viên bi màu đỏ. Trong túi ll cần có những viên bi có màu gì để biến cố "Người chơi thắng" là:
a) Biến cố chắc chắn;
b) Biến cố không thể;
c) Biến cố ngẫu nhiên?
Cho hai chiếc túi kín I, II đựng một số viên bi có cùng kích thước, trong đó tất cả các viên bi ở túi I có màu đen. Người chơi lấy ngẫu nhiên từ mỗi túi một viên bi và sẽ thắng nếu trong hai viên bi lấy ra có viên bi màu đỏ. Trong túi II cần có những viên bi màu gì để biến cố “ Người chơi thắng” là:a) Biến cố chắc chắn;b) Biến cố không thể;c) Biến cố ngẫu nhiên.
Đọc tiếp
Cho hai chiếc túi kín I, II đựng một số viên bi có cùng kích thước, trong đó tất cả các viên bi ở túi I có màu đen. Người chơi lấy ngẫu nhiên từ mỗi túi một viên bi và sẽ thắng nếu trong hai viên bi lấy ra có viên bi màu đỏ. Trong túi II cần có những viên bi màu gì để biến cố “ Người chơi thắng” là:
a) Biến cố chắc chắn;
b) Biến cố không thể;
c) Biến cố ngẫu nhiên.
a) Để biến cố “ Người chơi thắng” là biến cố chắc chắn thì người chơi luôn phải lấy được viên bi màu đỏ. Mà túi 1 toàn là bi đen nên túi 2 cần toàn là bi đỏ thì người chơi luôn lấy được bi đỏ
b) Để biến cố “ Người chơi thắng” là biến cố không thể thì người chơi luôn không lấy được viên bi màu đỏ. Vì túi 1 toàn là bi đen nên túi 2 không được có bi đỏ
c) Để biến cố “ Người chơi thắng” là biến cố ngẫu nhiên thì người chơi có thể lấy được viên bi màu đỏ. Mà túi 1 toàn là bi đen nên túi 2 cần có chứa bi đỏ và thêm bi màu khác.
Đúng 0
Bình luận (0)
Một túi đựng 10 bi đỏ và 5 bi xanh, chọn ngẫu nhiên 3 viên bi. Tính số cách để chọn được A) 3 viên bi xanh B) có đúng 1 viên bi màu đỏ C) có ít nhất 1 viên bi màu xanh
Bài 5.Một túi đựng 100 viên bi,mỗi viên bi có 1 trong 3 màu xanh,đỏ hoặc vàng.Biết rằng nếu lấy khỏi túi 75 viên bi bất kì thì luôn có 3 viên bi khác màu.Hỏi phải lấy ra ít nhất bao nhiêu viên bi để đảm bảo rằng trong số các viên bi được lấy ra có ít nhất 2 viên bi khác màu nhau.