cho nửa đường tròn o đường kính ab, 2 tia tiếp tuyến ax, by cùng thuộc 1 nửa mặt phẳng bờ ab có chứa nửa đường tròn. gọi o là 1 điểm nằm trên nửa đường tròn, qua m kẻ 1 đường thẳng vuông góc với cm cắt ã ở d, cắt by ở e a)cm: acmd, bcme nội tiếp b) am^2 = mk.mb c)so sánh góc mab, góc mec

Những câu hỏi liên quan
Cho nửa đường tròn (O;R), có đường kính AB. Kẻ 2 tia Ax, By vuông góc AB (Ax, By, nửa đường tròn (O) cùng thuộc 1 nửa mặt phẳng bờ chứa AB). Trên nửa đường tròn lấy M (M khác A, B), qua M kẻ tiếp tuyến với nửa đường tròn, nó cắt Ax, By theo thứ tự tại C, D.a, CM AC+BDCD.b, CM góc COD 90 độ.c, CM tích AC.BD không đổi khi M di chuyển trên nửa đường tròn.d, CB cắt DA tại K, MK cắt AB tại H. CM MK//AC//BD.e, CM K là trung điểm MH.f, CM AB là tiếp tuyến đường kính CD.
Đọc tiếp
Cho nửa đường tròn (O;R), có đường kính AB. Kẻ 2 tia Ax, By vuông góc AB (Ax, By, nửa đường tròn (O) cùng thuộc 1 nửa mặt phẳng bờ chứa AB). Trên nửa đường tròn lấy M (M khác A, B), qua M kẻ tiếp tuyến với nửa đường tròn, nó cắt Ax, By theo thứ tự tại C, D.
a, CM AC+BD=CD.
b, CM góc COD = 90 độ.
c, CM tích AC.BD không đổi khi M di chuyển trên nửa đường tròn.
d, CB cắt DA tại K, MK cắt AB tại H. CM MK//AC//BD.
e, CM K là trung điểm MH.
f, CM AB là tiếp tuyến đường kính CD.
a: Xét (O) có
CM là tiếp tuyến có M là tiếp điểm
CA là tiếp tuyến có A là tiếp điểm
Do đó: CM=CA
Xét (O) có
DM là tiếp tuyến có M là tiếp điểm
DB là tiếp tuyến có B là tiếp điểm
Do đó: DM=DB
Ta có: CM+MD=CD
nên CD=CA+DB
Đúng 0
Bình luận (2)
Cho nửa đường tròn (O;R), có đường kính AB. Kẻ hai tia Ax và By vuông góc với AB (Ax, By và nửa đường tròn (O) thuộc cùng một nửa mặt phẳng bờ chứa AB). Trên nửa đường tròn lấy điểm M (M khác A và B), qua M kẻ tiếp tuyến với nửa đường tròn, nó cắt Ax và By theo thứ tự tại C và D.
Chứng minh: a)AC + BD = CD
b) (góc) COD = AC + BD
Cho nửa đường tròn tâm O đường kính AB. Gọi Ax, By là các tia vuông góc với AB (Ax, By và nửa đường tròn thuộc cùng một nửa mặt phẳng bờ AB). Gọi C là 1 điểm bất kì trên nửa đường tròn ( C khác A,B ). qua C kẻ tiếp tuyến với nửa đường tròn cắt Ax, By tại M,N a. Tính MON b. Chứng minh rằng MN = AM + BN c. Chứng minh rằng AM.BN = R2
b: Xét (O) có
MC là tiếp tuyến
MA là tiếp tuyến
Do đó: MC=MA
Xét (O) có
NC là tiếp tuyến
NB là tiếp tuyến
Do đó: NC=NB
Ta có: MN=MC+NC
nên MN=MA+NB
Đúng 0
Bình luận (0)
Cho nửa đường tròn (O) đường kính AB a. Gọi Ax, By là các tia vuông góc với AB ( Ax, By thuộc cùng một nửa mặt phẳng bờ AB). Qua điểm M thuộc nửa đường tròn (O) (M khác A và B) kẻ tiếp tuyến với nửa đường tròn (O); nó cắt Ax, By lần lượt ở E và F.1. Chứng minh: góc EOF 90o2. Chứng minh tứ giác AEMO nội tiếp; hai tam giác MAB và OEF đồng dạng.3. Gọi K là giao điểm của AF và BE, chứng minh MK vuông góc AB.
Đọc tiếp
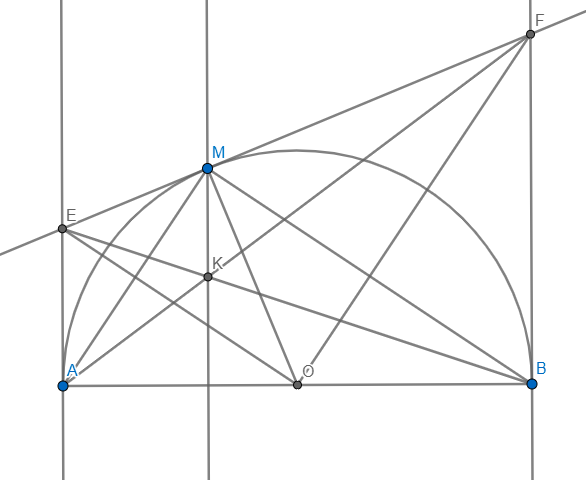
Cho nửa đường tròn (O) đường kính AB = a. Gọi Ax, By là các tia vuông góc với AB ( Ax, By thuộc cùng một nửa mặt phẳng bờ AB). Qua điểm M thuộc nửa đường tròn (O) (M khác A và B) kẻ tiếp tuyến với nửa đường tròn (O); nó cắt Ax, By lần lượt ở E và F.
1. Chứng minh: góc EOF = 90o
2. Chứng minh tứ giác AEMO nội tiếp; hai tam giác MAB và OEF đồng dạng.
3. Gọi K là giao điểm của AF và BE, chứng minh MK vuông góc AB.
1) Vì EM,EA là tiếp tuyến \(\Rightarrow OE\) là phân giác \(\angle MOA\)
\(\Rightarrow\angle MOE=\dfrac{1}{2}\angle MOA\)
Vì FM,FB là tiếp tuyến \(\Rightarrow OF\) là phân giác \(\angle MOB\)
\(\Rightarrow\angle MOF=\dfrac{1}{2}\angle MOB\)
\(\Rightarrow\angle MOE+\angle MOF=\dfrac{1}{2}\left(\angle MOA+\angle MOB\right)=\dfrac{1}{2}.180=90\)
\(\Rightarrow\angle EOF=90\)
2) Ta có: \(\angle EAO+\angle EMO=90+90=180\Rightarrow AEMO\) nội tiếp
\(\Rightarrow\angle MEO=\angle MAO\)
Vì AB là đường kính \(\Rightarrow\angle AMB=90\)
Xét \(\Delta MAB\) và \(\Delta OEF:\) Ta có: \(\left\{{}\begin{matrix}\angle AMB=\angle EOF\\\angle FEO=\angle MAB\end{matrix}\right.\)
\(\Rightarrow\Delta MAB\sim\Delta OEF\left(g-g\right)\)
Vì \(AE\parallel BF(\bot AB)\) \(\Rightarrow\dfrac{BF}{AE}=\dfrac{FK}{AK}\left(1\right)\)
Vì EM,EA là tiếp tuyến \(\Rightarrow EA=EM\left(2\right)\)
Vì FM,FB là tiếp tuyến \(\Rightarrow FB=FM\left(3\right)\)
Thế (2),(3) vào (1) \(\Rightarrow\dfrac{FM}{EM}=\dfrac{FK}{AK}\Rightarrow\) \(MK\parallel AE\) \(\Rightarrow MK\bot AB\)
Đúng 1
Bình luận (0)
Cho nửa đường tròn (O) đường kính AB. Gọi Ax; By là các tia vuông góc với AB.(Ax ; By và nửa đường tròn cùng thuộc một nửa mặt phẳng bờ AB).Qua điểm M thuộc nửa đường tròn ( M khác A và B), kẻ tiếp tuyến với nửa đường tròn, nó cắt Ax tại C và cắt By tại DA) c/m CDAC+BD và COD 90B) AD cắt BC tại N. Chứng minh: MN//BDC) Gọi H là trung điểm của AM. Chứng minh: ba điểm O, H , C thẳng hànggiúp tớ câu b và c thôi ạ
Đọc tiếp
Cho nửa đường tròn (O) đường kính AB. Gọi Ax; By là các tia vuông góc với AB.(Ax ; By và nửa đường tròn cùng thuộc một nửa mặt phẳng bờ AB).Qua điểm M thuộc nửa đường tròn ( M khác A và B), kẻ tiếp tuyến với nửa đường tròn, nó cắt Ax tại C và cắt By tại D
A) c/m CD=AC+BD và COD = 90
B) AD cắt BC tại N. Chứng minh: MN//BD
C) Gọi H là trung điểm của AM. Chứng minh: ba điểm O, H , C thẳng hàng
giúp tớ câu b và c thôi ạ
Cho nửa đường tròn tâm O, đường kính AB. Gọi Ax, By là các tia vuông góc với AB (Ax, By và nửa đường tròn thuộc cùng một nửa mặt phẳng bờ AB). Qua điểm M thuộc nửa đường tròn (M khác A,B), kẻ tiếp tuyến với nửa đường tròn, nó cắt Ax và By theo thứ tự ở C và D. Biết CDa và BD 3ACa) CMR: OC và OD vuông gócb) Tính tỉ số AC^2+BD^2/ CD^2c) Tính theo a diện tích tứ giác ACDB
Đọc tiếp
Cho nửa đường tròn tâm O, đường kính AB. Gọi Ax, By là các tia vuông góc với AB (Ax, By và nửa đường tròn thuộc cùng một nửa mặt phẳng bờ AB). Qua điểm M thuộc nửa đường tròn (M khác A,B), kẻ tiếp tuyến với nửa đường tròn, nó cắt Ax và By theo thứ tự ở C và D. Biết CD=a và BD= 3AC
a) CMR: OC và OD vuông góc
b) Tính tỉ số AC^2+BD^2/ CD^2
c) Tính theo a diện tích tứ giác ACDB
Bài 5. Cho nửa đường tròn (O) đường kính AB. Gọi Ax; By là các tia vuông góc với AB.(Ax ; By và nửa đường tròn cùng thuộc một nửa mặt phẳng bờ AB).Qua điểm M thuộc nửa đường tròn ( M khác A và B), kẻ tiếp tuyến với nửa đường tròn, nó cắt Ax tại C và cắt By tại D.a) Chứng minh và b) AD cắt BC tại N. Chứng minh: c) Tích AC.BD không đổi khi điểm M di chuyển trên nửa đường tròn.d) Gọi H là trung điểm của AM. Chứng minh: ba điểm O, H , C thẳng hàng.Thu gọn
Đọc tiếp
Bài 5. Cho nửa đường tròn (O) đường kính AB. Gọi Ax; By là các tia vuông góc với AB.(Ax ; By và nửa đường tròn cùng thuộc một nửa mặt phẳng bờ AB).Qua điểm M thuộc nửa đường tròn ( M khác A và B), kẻ tiếp tuyến với nửa đường tròn, nó cắt Ax tại C và cắt By tại D.
a) Chứng minh
và
b) AD cắt BC tại N. Chứng minh:
c) Tích AC.BD không đổi khi điểm M di chuyển trên nửa đường tròn.
d) Gọi H là trung điểm của AM. Chứng minh: ba điểm O, H , C thẳng hàng.
Thu gọn
Bài 5. Cho nửa đường tròn (O) đường kính AB. Gọi Ax; By là các tia vuông góc với AB.(Ax ; By và nửa đường tròn cùng thuộc một nửa mặt phẳng bờ AB).Qua điểm M thuộc nửa đường tròn ( M khác A và B), kẻ tiếp tuyến với nửa đường tròn, nó cắt Ax tại C và cắt By tại D.a) Chứng minh và b) AD cắt BC tại N. Chứng minh: c) Tích AC.BD không đổi khi điểm M di chuyển trên nửa đường tròn.d) Gọi H là trung điểm của AM. Chứng minh: ba điểm O, H , C thẳng hàng.
Đọc tiếp
Bài 5. Cho nửa đường tròn (O) đường kính AB. Gọi Ax; By là các tia vuông góc với AB.(Ax ; By và nửa đường tròn cùng thuộc một nửa mặt phẳng bờ AB).Qua điểm M thuộc nửa đường tròn ( M khác A và B), kẻ tiếp tuyến với nửa đường tròn, nó cắt Ax tại C và cắt By tại D.
a) Chứng minh và
b) AD cắt BC tại N. Chứng minh:
c) Tích AC.BD không đổi khi điểm M di chuyển trên nửa đường tròn.
d) Gọi H là trung điểm của AM. Chứng minh: ba điểm O, H , C thẳng hàng.
:. Cho nửa đường tròn (O), đường kính AB 2R. Gọi Ax, By là các tia vuông góc với AB (Các tia Ax, By và nửa đường tròn thuộc cùng một nửa mặt phẳng bờ AB). Qua điểm I thuộc nửa đường tròn (I khác A và B) kẻ tiếp tuyến với nửa đường tròn (O), nó cắt các tia Ax, By lần lượt ở M và N. a) Chứng minh:góc MON90 độ b) Chứng minh : MN AM + BN. c) Chứng minh AB là tiếp tuyến của đường tròn đường kính MN. d) Xác định vị trí của điểm I trên nửa đường tròn (O) để diện tích tứ giác...
Đọc tiếp
:. Cho nửa đường tròn (O), đường kính AB = 2R. Gọi Ax, By là các tia vuông góc với AB (Các tia Ax, By và nửa đường tròn thuộc cùng một nửa mặt phẳng bờ AB). Qua điểm I thuộc nửa đường tròn (I khác A và B) kẻ tiếp tuyến với nửa đường tròn (O), nó cắt các tia Ax, By lần lượt ở M và N.
a) Chứng minh:góc MON=90 độ
b) Chứng minh : MN = AM + BN.
c) Chứng minh AB là tiếp tuyến của đường tròn đường kính MN.
d) Xác định vị trí của điểm I trên nửa đường tròn (O) để diện tích tứ giác AMNB đạt giá trị nhỏ nhất.
a: Xét (O) có
MI,MA là tiếp tuyến
nên MI=MA và OM là phân giác của góc AOI(1)
Xét (O) có
NI,NB là tiếp tuyến
nên NI=NB và ON là phân giác của góc IOB(2)
Từ (1), (2) suy ra góc MON=1/2*180=90 độ
b: MN=MI+IN
=>MN=MA+NB
c: Gọi H là trung điểm của MN
Xét hình thang AMNB có
O,H lần lượt là trung điểm của AB,MN
nên HO là đường trung bình
=>HO//AM//BN
=>HO vuông góc AB
=>AB là tiếp tuyến của(H)
Đúng 0
Bình luận (0)
Cho nửa đường tròn tâm O đường kính AB. Gọi Ax, By là các tia vuông góc với AB (Ax, By và nửa đường tròn thuộc cùng một nửa mặt phẳng bờ AB). Gọi M là điểm bất kì thuộc tia Ax. Qua M kẻ tiếp tuyến với nửa đường tròn, cắt By ở N.a. Tính số đo góc MONb. Chứng minh rằng MN AM + BNc. Chứng minh rằng AM.BN R2 (R là bán kính của nửa đường tròn)giúp với ạ
Đọc tiếp
Cho nửa đường tròn tâm O đường kính AB. Gọi Ax, By là các tia vuông góc với AB (Ax, By và nửa đường tròn thuộc cùng một nửa mặt phẳng bờ AB). Gọi M là điểm bất kì thuộc tia Ax. Qua M kẻ tiếp tuyến với nửa đường tròn, cắt By ở N.
a. Tính số đo góc MON
b. Chứng minh rằng MN = AM + BN
c. Chứng minh rằng AM.BN = R2 (R là bán kính của nửa đường tròn)
giúp với ạ
bạn tự vẽ hình giúp mik nha
a) áp dụng t/c 2 tiếp tuyến cắt nhau ta có
OM là tia phân giác \(\widehat{AOI}\)
ON là tpg \(\widehat{IOB}\)
mà:\(\widehat{AOI}+\widehat{BOI}=180^o\)\(\Rightarrow OM\perp ON\)(t/c 2 góc kề bù)
vậy \(\widehat{MON}=90^o\)
b)từ t/c 2 tiếp tuyến cắt nhau ta có
MA=MI;BN=NI
\(\Rightarrow\)AM+BN=MI+NI=MN9(đpcm)
c)ta có:AM.BN=MI.NI(1)
xét \(\Delta MON\) vuông tại O có
MI.NI(đlý)=\(OI^2=R^2\)(2)
từ (1) và (2)\(\Rightarrow AM.BN=R^2\)
Đúng 0
Bình luận (0)
















