1) Cho tam giác ABC cân tại A nội tiếp đường tròn (O;R). Qua A kẻ đường thẳng cắt cạnh BC tại D và cắt (O) tại E.
a) Chứng minh EA là tia phân giác góc BEC.
b) Chứng minh tg AEB đồng dạng với tg ABD và suy ra tích AD. AE không đổi.
Những câu hỏi liên quan
Cho tam giác ABC cân tại A nội tiếp đường tròn (O) , cạnh bên bằng b. Tính bán kính đường tròn nội tiếp tam giác
cho tam giác abc nội tiếp đường tròn (o), I là tâm đường tròn nội tiếp tam giác abc. AI cắt (o) tại M, c/m tam giác MIB cân
Cho tam giác ABC cân tại A nội tiếp đường tròn (O), cạnh AB = a, đường cao AH = h. Tính
bán kính đường tròn ngoại tiếp tam giác theo a và h.
Cho tam giác ABC cân tại A nội tiếp đường tròn O đường kính AI gọi E là trung điểm của AB K là trung điểm của OI
a, CMR: tam giác EKB cân
b, tứ giác AEKC nội tiếp đường tròn
Cho tam giác ABC cân tại A nội tiếp đường tròn (O), cạnh bên bằng b, đường cao
AH=h. Tính bán kính đường tròn (O).
Kéo dài AH cắt đường tròn tại D \(\Rightarrow\) AD là đường kính
\(\Rightarrow\widehat{ABD}\) là góc nội tiếp chắn nửa đường tròn hay tam giác ABD vuông tại B
Áp dụng hệ thức lượng:
\(AB^2=AH.AD\Rightarrow AD=\dfrac{AB^2}{AH}=\dfrac{b^2}{h}\)
\(\Rightarrow2R=\dfrac{b^2}{h}\Rightarrow R=\dfrac{b^2}{2h}\)
Đúng 0
Bình luận (0)
cho tam giác ABC nhọn nội tiếp đường tròn (O). Hai đường cao AM ,BN cắt nhau tại H và cắt đường tròn (O) lần lượt tại D,E. chứng minh rằng
a. tứ giác HMCN nội tiếp đường tròn
b. CD=CE
c. tam giác BHD cân
a: góc HMC+góc HNC=180 độ
=>HMCN nội tiếp
b: góc CAD=góc NBC
=>1/2*sđ cung CD=1/2*sđ cung CE
=>CD=CE
c: góc BHM=góc BCN=1/2*sđ cung BA
góc BDH=1/2*sđ cung BA
=>góc BHD=góc BDH
=>ΔBHD cân tại B
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A nội tiếp đường tròn (O), cạnh bên bằng 10a, đường cao AH bằng
8a. Tính bán kính đường tròn (O).
Kẻ đường kính AD thì góc ACD = 90°
Ta có AC²= AD.AH nên AD = AC²/AH
<=>AD= (10a)²/ 8a=100a/8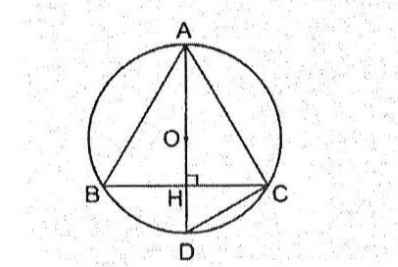
Đúng 1
Bình luận (0)
cho đường tròn tâm o nội tiếp tam giác ABC cân tại A đường cao AH cắt đường tròn tâm o tại D chứng minh BC.BC=4AH.DH
các bạn giúp mình nhé sáng thứ tư mình nộp bài rồi cảm ơn
Đúng 0
Bình luận (0)
5 tháng 2 2022 lúc 9:55
Tam giác ABC vuông cân tại A và nội tiếp trong đường tròn tâm O bán kính R. Gọi r là bán kính đường tròn nội tiếp tam giác ABC. Khi đó tỉ số \(\dfrac{R}{r}\) bằng
Giải chi tiết cho mk vs
Tham khảo:
Ta có: \(R=\dfrac{abc}{4S};r=\dfrac{S}{p}\)
Vì tam giác ABC vuông cân tại A nên \(b=c\) và \(a=\sqrt{b^2+c^2}=b\sqrt{2}\)
Xét tỉ số:
\(\dfrac{R}{r}=\dfrac{abc.p}{4S^2}=\dfrac{abc.\dfrac{a+b+c}{2}}{4.\dfrac{1}{4}.\left(b.c\right)^2}=\dfrac{a\left(a+2b\right)}{2b^2}=\dfrac{2b^2\left(1+\sqrt{2}\right)}{2b^2}=1+\sqrt{2}\)
Đúng 0
Bình luận (3)
\(\dfrac{R}{r}=\dfrac{abc.p}{4S^2}=\dfrac{abc.\dfrac{a+b+c}{2}}{4.\dfrac{1}{4}\left(b.c\right)^2}=\dfrac{a.b^2\dfrac{\left(a+2b\right)}{2}}{b^4}=\dfrac{a.b^2\left(a+2b\right)}{2b^4}=\dfrac{a\left(a+2b\right)}{2b^2}\)
\(=\dfrac{b\sqrt{2}\left(b\sqrt{2}+2b\right)}{2b^2}=\dfrac{b^2\sqrt{2}\left(\sqrt{2}+2\right)}{2b^2}=\dfrac{2b^2\left(1+\sqrt{2}\right)}{2b^2}=1+\sqrt{2}\)
Đúng 3
Bình luận (1)
Cho tam giác ABC cân tại A, đ tròn (O) ngoại tiếp tam giác ABC, đường tròn tâm (O') tiếp xúc trong với (O) và tiếp xúc với cạnh AB ở P, AC ở Q. Cm trung điểm I của PQ là tâm đ tròn nội tiếp tam giác ABC