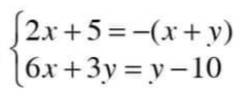
giải hệ ptrinh
Cho hệ phương trình \(\left\{{}\begin{matrix}mx+y=1\\x+my=2\end{matrix}\right.\)
a) Giải hệ ptrinh khi m=2
b) Giải và biểu diễn hệ ptrinh theo tham số m
c) Tìm m để hệ ptrinh có (x;y) thỏa mãn x-y=1
d) Tìm hệ thức liên hệ giữa x và y không phụ thuộc vào m
Giai bài toán bằng cách lập hệ ptrinh hoặc ptrinh:
Chu vi của 1 tam giác bằng 48cm. Biết cạnh lớn nhất bằng 20cm, hai cạnh còn lại hơn kém nhau 2 đơn vị. Tìm độ dài 2 cạnh đó ??
P/s: Cần lời giải chi tiết ạ :33
Gọi cạnh lớn hơn trong hai cạnh còn lại là a (a > 2)
Cạnh bé hơn trong hai cạnh còn lại là b (b > 0)
Tổng hai cạnh còn lại này là \(48-20=28\left(cm\right)\)
Theo đề bài, ta có hệ phương trình:
\(\hept{\begin{cases}a+b=28\\a-b=2\end{cases}}\Leftrightarrow\hept{\begin{cases}a=15\\b=13\end{cases}}\)
Vậy độ dài hai cạnh còn lại lần lượt dài \(15cm\) và \(13cm\)
Hệ ptrinh : (m+1)x-(m+1)y=4m (1) x+(m-2)y =2. (2) tìm điều kiện của m đe ptrinh có nghiệm duy nhất . Tìm nghiệm duy nhat đó
Lời giải:
a) Khi $m=2$ thì pt trở thành:
$x^2-10x+15=0\Leftrightarrow (x-5)^2=10\Rightarrow x=5\pm \sqrt{10}$
b)
Để pt có 2 nghiệm pb $x_1,x_2$ thì trước tiên:
$\Delta'=(2m+1)^2-(4m^2-2m+3)>0$
$\Leftrightarrow 6m-2>0\Leftrightarrow m>\frac{1}{3}$
Áp dụng định lý Viet: \(\left\{\begin{matrix} x_1+x_2=2(2m+1)\\ x_1x_2=4m^2-2m+3\end{matrix}\right.\)
Để $(x_1-1)^2+(x_2-1)^2+2(x_1+x_2-x_1x_2)=18$
$\Leftrightarrow x_1^2+x_2^2-2(x_1+x_2)+2+2(x_1+x_2-x_1x_2)=18$
$\Leftrightarrow x_1^2+x_2^2-2x_1x_2=16$
$\Leftrightarrow (x_1+x_2)^2-4x_1x_2=16$
$\Leftrightarrow 4(2m+1)^2-4(4m^2-2m+3)=16$
$\Leftrightarrow (2m+1)^2-(4m^2-2m+3)=4$
$\Leftrightarrow 6m-2=4\Leftrightarrow m=1$ (thỏa mãn)
vậy...........
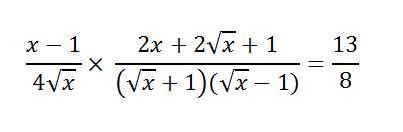
giải bất ptrinh hộ mình với
ĐKXĐ: \(\left\{{}\begin{matrix}x>0\\x\ne1\end{matrix}\right.\)
\(\dfrac{x-1}{4\sqrt{x}}\cdot\dfrac{2x+2\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}=\dfrac{13}{8}\)
=>\(\dfrac{\left(x-1\right)}{4\sqrt{x}}\cdot\dfrac{2x+2\sqrt{x}+1}{x-1}=\dfrac{13}{8}\)
=>\(\dfrac{2x+2\sqrt{x}+1}{4\sqrt{x}}=\dfrac{13}{8}\)
=>\(8\left(2x+2\sqrt{x}+1\right)=13\cdot4\sqrt{x}=52\sqrt{x}\)
=>\(16x+16\sqrt{x}+16-52\sqrt{x}=0\)
=>\(16x-36\sqrt{x}+16=0\)
=>\(4x-9\sqrt{x}+4=0\)
=>\(x-\dfrac{9}{4}\sqrt{x}+1=0\)
=>\(x-2\cdot\sqrt{x}\cdot\dfrac{9}{8}+\dfrac{81}{64}-\dfrac{17}{64}=0\)
=>\(\left(\sqrt{x}-\dfrac{9}{8}\right)^2-\dfrac{17}{64}=0\)
=>\(\left(\sqrt{x}-\dfrac{9}{8}-\dfrac{\sqrt{17}}{8}\right)\left(\sqrt{x}-\dfrac{9}{8}+\dfrac{\sqrt{17}}{8}\right)=0\)
=>\(\left[{}\begin{matrix}\sqrt{x}-\dfrac{9}{8}-\dfrac{\sqrt{17}}{8}=0\\\sqrt{x}-\dfrac{9}{8}+\dfrac{\sqrt{17}}{8}=0\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}\sqrt{x}=\dfrac{9+\sqrt{17}}{8}\\\sqrt{x}=\dfrac{9-\sqrt{17}}{8}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{49+9\sqrt{17}}{32}\left(nhận\right)\\x=\dfrac{49-9\sqrt{17}}{32}\left(nhận\right)\end{matrix}\right.\)
Giải ptrinh 4+x/5=5/3
\(4+\dfrac{x}{5}=\dfrac{5}{3}\\ \Rightarrow\dfrac{x}{5}=-\dfrac{7}{3}\\ \Rightarrow x=-\dfrac{35}{3}\)
\(4+\dfrac{x}{5}=\dfrac{5}{3}\)
=>\(\dfrac{x}{5}=\dfrac{5}{3}-4=-\dfrac{7}{3}\)
=>x=-7/3*5=-35/3
giải hệ ptrinh
a)\(\left\{{}\begin{matrix}5x+2y=4\\x-2y=8\end{matrix}\right.\)
b)\(\left\{{}\begin{matrix}x-2y=2\\\dfrac{x}{2}+\dfrac{y}{3}=1\end{matrix}\right.\)
a)Cộng hai pt, ta được:
6x=12\(\Leftrightarrow x=2\)
Thay vào (1), ta có: y=-3.
Vậy hpt có nghiệm (2;-3).
b) Nhân pt 2 với 6, ta được: 3x+2y=6.
Cộng 2 pt ta được: 4x=8\(\Leftrightarrow x=2\)
Thay vào pt 1, ta được : y=0.
Vậy hpt có nghiệm là (2;0).
Giải như thế này cho dễ nhìn nhé:
a, \(\left\{{}\begin{matrix}5x+2y=4\\x-2y=8\end{matrix}\right.\)
⇔\(\left\{{}\begin{matrix}5x+2y=4\\5x-10y=40\end{matrix}\right.\)
⇔\(\left\{{}\begin{matrix}x=4\\y=-2\end{matrix}\right.\)
Vậy hệ phương trình có 2 nghiệm: \(\left\{{}\begin{matrix}x=4\\y=-2\end{matrix}\right.\)
b, \(\left\{{}\begin{matrix}x-2y=2\\\dfrac{x}{2}+\dfrac{y}{3}=1\end{matrix}\right.\)
⇔\(\left\{{}\begin{matrix}6x-12y=12\\\dfrac{6x}{2}+\dfrac{6y}{3}=6\end{matrix}\right.\)
⇔\(\left\{{}\begin{matrix}x=2\\y=0\end{matrix}\right.\)
Vậy hệ phương trình có 2 nghiệm :\(\left\{{}\begin{matrix}x=2\\y=0\end{matrix}\right.\)
giải ptrinh (x-1)^2=2(x^2-1)
\(\left(x-1\right)^2=2.\left(x^2-1\right)\\ \Leftrightarrow x^2-2x+1=2x^2-2\\ \Leftrightarrow2x^2-x^2+2x-2-1=0\\ \Leftrightarrow x^2+2x-3=0\\ \Leftrightarrow x^2+3x-x-3=0\\ \Leftrightarrow x.\left(x+3\right)-\left(x+3\right)=0\\ \Leftrightarrow\left(x-1\right).\left(x+3\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x-1=0\\x+3=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-3\end{matrix}\right.\\ \Rightarrow S=\left\{-3;1\right\}\)
3x-6x-3/4=5x-7/6 giải ptrinh
\(3x-6x-\dfrac{3}{4}=5x-\dfrac{7}{6}\)
\(\Leftrightarrow-3x-\dfrac{3}{4}=5x-\dfrac{7}{6}\)
\(\Leftrightarrow-3x-5x=-\dfrac{7}{6}+\dfrac{3}{4}\)
\(\Leftrightarrow-8x=-\dfrac{5}{12}\)
\(\Leftrightarrow x=-\dfrac{5}{12}:-8=\dfrac{5}{96}\)
Trong mặt phẳng với hệ trục tọa độ Oxy có tam giác ABC có a(1;4) tiếp tuyến tại A cùa đường tròn ngoại tiếp tam gia1`c ABC cắt BC tãi D,đường phân giác trong góc ABD ptrinh: x-y+2=0 co điểm M(-4;10 thuộc cạnh AC.viết ptrinh đường thẳng AB