\(\dfrac{x}{0}\) và x - 1 đâu không phải là phân thức đại số

Những câu hỏi liên quan
CâuNội dungĐúngSai1dfrac{x^5+1}{sqrt{x}-1}là một phân thức đại số 2dfrac{left(x+1right)^2}{1+x}dfrac{1+x}{-1} 3Phân thức nghịch đảo của phân thức dfrac{x}{x-2}là dfrac{x-2}{x} 4Điều kiện xác định của phân thức dfrac{x}{x^3-x}là x khác 0; x khác 1; x khác -1
Đọc tiếp
Câu | Nội dung | Đúng | Sai |
1 | \(\dfrac{x^5+1}{\sqrt{x}-1}\)là một phân thức đại số |
|
|
2 | \(\dfrac{\left(x+1\right)^2}{1+x}=\dfrac{1+x}{-1}\) |
|
|
3 | Phân thức nghịch đảo của phân thức \(\dfrac{x}{x-2}\)là \(\dfrac{x-2}{x}\) |
|
|
4 | Điều kiện xác định của phân thức \(\dfrac{x}{x^3-x}\)là x khác 0; x khác 1; x khác -1 |
|
|
Lời giải:
1. Đúng
2. Sai
3. Đúng
4. Đúng
Đúng 0
Bình luận (0)
Cho các biểu thức:
\(\dfrac{1}{a}x^2y^3\); \(2ax^2y^3\); \(\left(a+1\right)x^2y^3\); \(\dfrac{3a}{x}x^2\); \(\dfrac{2a}{y}y^3\)
Gọi a là hằng số; x,y là biến thì trong các biêu thức trên đâu là đơn thức và các đơn thức đó có đồng dạng không?
Kiểm tra xem:
a) \(x = - \dfrac{1}{8}\) có phải là nghiệm của đa thức P(x) = 4x + \(\dfrac{1}{2}\) không?
b) Trong ba số 1; -1 và 2, số nào là nghiệm của đa thức Q(x) = x2 + x – 2 ?
a) Ta có: P(\( - \dfrac{1}{8}\)) = 4.(\( - \dfrac{1}{8}\))+ \(\dfrac{1}{2}\)= (-\(\dfrac{1}{2}\)) + \(\dfrac{1}{2}\) = 0
Vậy \(x = - \dfrac{1}{8}\) là nghiệm của đa thức P(x) = 4x + \(\dfrac{1}{2}\)
b) Q(1) = 12 +1 – 2 = 0
Q(-1) = (-1)2 + (-1) – 2 = -2
Q(2) = 22 + 2 – 2 = 4
Vì Q(1) = 0 nên x = 1 là nghiệm của Q(x)
Đúng 1
Bình luận (0)
Bài 1. Trong các biểu thức sau, biểu thức nào là phân thức đại số
A. \(\dfrac{\dfrac{1}{2}x+5}{3x^3+3x+12}\) B. \(\dfrac{\dfrac{1}{x}}{2x+5}\) C. 4x2 – 5y D. \(\dfrac{1+\dfrac{1}{x}}{2-\dfrac{2}{x}}\)
Định nghĩa phân thức đại số. Một đa thức có phải là một phân thức đại số không ? Một số thực bất kì có phải là một phân thức đại số không ?
- Phân thức đại số (phân thức) là một biểu thức có dạng
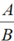
trong đó A, B là những đa thức, B ≠ 0. A là tử thức, B là mẫu thức.
- Một đa thức được coi như một phân thức với mẫu thức bằng 1.
- Một số thực a bất kì cũng là một phân thức đại số.
Đúng 0
Bình luận (0)
Định nghĩa phân thức đại số. Một đa thức có phải là phân thức đại số không ? Một số thực bất kì có phải là một phân thức đại số không ?
-Định nghĩa:Một phân thức đại số(hay nói gọn là phân thức)là một biểu thức có dạng\(\dfrac{A}{B}\),trong đó A,B là những đa thức và B khác đa thức 0.A được gọi là tử thức (hay tử) , B gọi là mẫu thức (hay mẫu).
-Mỗi đa thức cũng được coi như một phân thức với mẫu thức bằng 1.
-Chỉ có số 0, số 1 là những phân thức đại số.
Đúng 0
Bình luận (0)
*Một phân thức đại số(hay nói gọn là phân thức)là một biểu thức có dạng A/B,trong đó A,B là những đa thức và B khác đa thức 0.A được gọi là tử thức (hay tử) , B gọi là mẫu thức (hay mẫu).
-Mỗi đa thức cũng được coi như một phân thức với mẫu thức bằng 1.
-Chỉ có số 0, số 1 là những phân thức đại số.
Đúng 0
Bình luận (0)
câu1:Định nghĩa phân thức đại số.Một đa thức có phải là phân thức đại só không?Một số thực bất kì có phải là 1 phân thức đại số không?
câu2:Định nghĩa hai phân thức đại só ngang bằng nhau
câu3:Phát biểu tính chất cơ bản của phân thức đại số
câu4:neu quy tắc rút gọn 1 phân thứcs đai số.Hãy rút gọn phân thức \(\frac{8x-4}{8x^3-1}\)
Biểu thức nào sau đây không phải là đa thức
A. \(\sqrt 2 {x^2}y\)
B. \( - \dfrac{1}{2}x{y^2} + 1\)
C. \(\dfrac{1}{{2z}}x + y\)
D. 0
Các biểu thức không phải đa thức là:
\(\sqrt{2}x^2y,0\)
Đúng 1
Bình luận (0)
Đại lượng x lấy các giá trị là các số tự nhiên, đại lượng y lấy giá trị là số dư phép chia x cho 3. Đại lượng y có phải là hàm số của đại lượng x không?Đại lượng x lấy các giá trị là các số tự nhiên, đại lượng y lấy giá trị là ước của x. Đại lượng y có phải là hàm số của đại lượng x không?CMR: a)Tổng của 1 số hữu tỉ và 1 số vô tỉ là 1 số vô tỉb) Tích của một số hữu tỉ khác 0 với 1 số vô tỉ là 1 số VTc) Thương của 1 số HT với 1 số VT là 1 số VT
Đọc tiếp
Đại lượng x lấy các giá trị là các số tự nhiên, đại lượng y lấy giá trị là số dư phép chia x cho 3. Đại lượng y có phải là hàm số của đại lượng x không?
Đại lượng x lấy các giá trị là các số tự nhiên, đại lượng y lấy giá trị là ước của x. Đại lượng y có phải là hàm số của đại lượng x không?
CMR: a)Tổng của 1 số hữu tỉ và 1 số vô tỉ là 1 số vô tỉ
b) Tích của một số hữu tỉ khác 0 với 1 số vô tỉ là 1 số VT
c) Thương của 1 số HT với 1 số VT là 1 số VT
1.Đại lượng y là hàm số của đại lượng x vì ta có mỗi giá trị của đại lượng x đều có một giá trị tương ứng của đại lượng y . Giá trị tương ứng ấy của đại lượng y là duy nhất.
2. Đại lượng y không phải là hàm số của đại lượng x vì ứng với giá trị x = 5 chẳng hạn ta có hai giá trị của y (ước tự nhiên của 5 là 1 và 5)
3. Dựa vào định nghĩa các phép toán về số hữu tỉ. Chú ý rằng với các số hữu tỉ thì kết quả của các phép toán này là số hữu tỉ. Chẳng hạn câu b). Giả sử tích của số hữu tỉ \(x\ne0\)với số vô tỉ y là số hữu tỉ z. Ta có x.y=z.
Như vậy thì \(y=\frac{z}{x}\). Nhưng z và x \(\left(x\ne0\right)\)là hai số hữu tỉ nên thương của chúng cũng là số hữu tỉ. Suy ra y là số hữu tỉ, trái với đề bài. Vậy tích của một số hữu tỉ khác 0 với một số vô tỉ là một số vô tỉ.
Đúng 0
Bình luận (0)




















