Cho hình chóp tứ giác đều có tất cả các cạnh bên, cạnh đáy là a. Tính chiều cao của hình chóp?

Những câu hỏi liên quan
Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng 3. Tính diện tích xung quanh của hình nón có đáy là đường tròn ngoại tiếp tứ giác ABCD và chiều cao bằng chiều cao của hình chóp.
Đọc tiếp
Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng 3. Tính diện tích xung quanh của hình nón có đáy là đường tròn ngoại tiếp tứ giác ABCD và chiều cao bằng chiều cao của hình chóp.
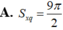
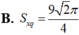
![]()
Cho hình chóp tứ giác đều có tất cả các cạnh đều bằng a. Tính cosin của góc giữa mặt bên với mặt đáy của hình chóp.
A. 1 3
B. 1 3
C. 1 2
D. 1 2
Đáp án A
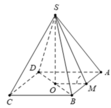
Xét hình chóp tứ giác đều S.ABCD có các cạnh bằng a.
Gọi O là tâm hình vuông ABCD, M là trung điểm của AB.
Khi đó S O ⊥ A B O M ⊥ A B ⇒ A B ⊥ S M O ⇒ S A B ; A B C D ^ = S M O ^
Tam giác SMO vuông tại O, có c o s S M O ^ = O M S M = a 2 : a 3 2 = 3 3
Vậy c o s S A B ; A B C D ^ = 3 3
Đúng 0
Bình luận (0)
Cho hình chóp cụt tứ giác đều ABCD.A'B'C'D' có các cạnh đáy là a và 2 a, chiều cao của mặt bên là a
a) Tính diện tích xung quanh của hình chóp cụt
b) Tính độ dài cạnh bên và chiều cao hình chóp cụt
\(a,S_{xp}=4.\dfrac{a+2a}{2}.a=6a^2\)
\(b,\)Vẽ một mặt bên. Ta có:\(AH=\dfrac{AB-A^'B^'}{2}=\dfrac{2a-a}{2}=\dfrac{a}{2}\)
Trong tamn giác vuông A'HA:
\(AA^'=\sqrt{a^2+\left(\dfrac{a}{2}\right)^2}=\sqrt{\dfrac{5a^2}{4}}\)
Từ đó tính tiếp sẽ ra chiều cao hình chóp
Đáp số :Độ dài cạnh bên là :\(\sqrt{\dfrac{5a^2}{4}}\)
Chiều cao chóp cụt :\(\sqrt{\dfrac{3a^2}{4}}\)
Đúng 0
Bình luận (0)
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a, tất cả các cạnh bên tạo với mặt phẳng đáy một góc
60
o
. Thể tích của khối chóp S.ABCD là
Đọc tiếp
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a, tất cả các cạnh bên tạo với mặt phẳng đáy một góc 60 o . Thể tích của khối chóp S.ABCD là



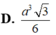
Hình chóp tứ giác đều S.ABCD có đáy là hình vuông cạnh a, các mặt bên của mình chóp là các tam giác đều. Tính đường cao SH của hình chóp đó. A. SH
a
3
2
B. SH
a
2
C. SH
a
2
2
D. SH
a
2
3
Đọc tiếp
Hình chóp tứ giác đều S.ABCD có đáy là hình vuông cạnh a, các mặt bên của mình chóp là các tam giác đều. Tính đường cao SH của hình chóp đó.
A. SH = a 3 2
B. SH = a 2
C. SH = a 2 2
D. SH = a 2 3
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy AB = 20cm, cạnh bên SA = 24cm.
a) Tính chiều cao SO rồi tính thể tích của hình chóp.
b) Tính diện tích toàn phần của hình chóp.
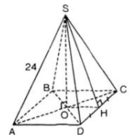
a) S.ABCD là hình chóp tứ giác đều
⇒ ABCD là hình vuông
⇒ AC = AB√2 = 20√2 (cm).
SO là chiều cao của hình chóp
⇒ O = AC ∩ BD và SO ⊥ (ABCD)
⇒ SO ⊥ AO
⇒ ΔSAO vuông tại O
⇒ SO2 + OA2 = SA2
⇒ SO2 = SA2 – OA2 = SA2 – (AC/2)2 = 242 - 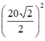 = 376
= 376
⇒ SO = √376 ≈ 19,4 (cm).
Thể tích hình chóp:
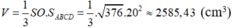
b) Gọi H là trung điểm của CD
SH2 = SD2 – DH2 = 242 – 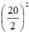 = 476
= 476
⇒ SH = √476 ≈ 21,8 (cm)
⇒ Sxq = p.d = 2.AB.SH = 2.20.√476 ≈ 872,7 (cm2 ).
Sđ = AB2 = 202 = 400 (cm2 )
⇒ Stp = Sxq + Sđ = 872,7 + 400 = 1272,7 (cm2 ).
Đúng 0
Bình luận (0)
Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng a . Tính góc giữa cạnh bên và mặt đáy .
Cho hình chóp tứ giác đều S.ABCD các cạnh đáy bằng a, góc giữa cạnh bên SA và mặt đáy bằng
30
o
. Tính diện tích xung quanh
S
x
q
của hình trụ có một đường tròn đáy là đường tròn nội tiếp hình vuông ABCD và chiều cao bằng chiều cao của hình chóp S.ABCD A.
S
x
q
π...
Đọc tiếp
Cho hình chóp tứ giác đều S.ABCD các cạnh đáy bằng a, góc giữa cạnh bên SA và mặt đáy bằng 30 o . Tính diện tích xung quanh S x q của hình trụ có một đường tròn đáy là đường tròn nội tiếp hình vuông ABCD và chiều cao bằng chiều cao của hình chóp S.ABCD
A. S x q = π a 2 6 12
B. S x q = π a 2 3 12
C. S x q = π a 2 3 6
D. S x q = π a 2 6 6
a) Tính diện tích xung quanh của hình chóp tam giác đều có độ dài cạnh đáy là 1010cm, chiều cao của mặt bên xuất phát từ đỉnh của hình chóp tam giác đều là 1212cm.
b) Tính diện tích toàn phần và thể tích của hình chóp tứ giác đều có độ dài cạnh đáy là 7272dm, chiều cao là 68,168,1dm, chiều cao của mặt bên xuất phát từ đỉnh của hình chóp tứ giác đều là 7777dm.
a) Diện tích xung quanh của hình chóp tam giác đều là: \(\frac{{10.3}}{2}.12 = 180\) (\(c{m^2}\))
b) Diện tích xung quanh của hình chóp tứ giác đều là: \(\frac{{72.4}}{2}.77 = 11088\) (\(d{m^2}\))
Diện tích đáy của hình chóp tứ giác đều là: \({72^2}=5184\) (\(d{m^2}\))
Diện tích toàn phần của hình chóp tứ giác đều là: \(11088 + 5184 = 16 272\) (\(d{m^2}\))
Thể tích của hình chóp tứ giác đều là: \(\frac{1}{3}.5184.68,1=117676,8\) (\(d{m^3}\))
Đúng 1
Bình luận (0)