Bài 1: Cho đoạn thẳng AB. Gọi d là đường trung trực của AB. Trên d lấy 1 điểm M bất kì. Chứng minh MA=MB. Từ đó suy ra tính chất đường trung trực của 1 đoạn thẳng

Những câu hỏi liên quan
Cho đoạn thẳng AB có O là trung điểm và d là đường trung trực. Lấy điểm M tùy ý thuộc d (Hình 5). Chứng minh rằng hai tam giác MOA và MOB bằng nhau, từ đó suy ra MA = MB
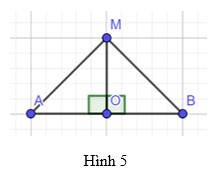
Theo giả thiết ta có O là trung điểm AB \( \Rightarrow \) AO = OB
Xét tam giác AOM và tam giác BOM có :
OM là cạnh chung
AO = OB
\(\widehat {MOA} = \widehat {MOB} = {90^o}\)(do d là trung trực AB)
(c-g-c)
\( \Rightarrow MA = MB\) (cạnh tương ứng)
Đúng 0
Bình luận (0)
Cho đoạn thẳng AB, gọi d là đường trung trực của AB, trên d lấy điểm M bất kì
a) So sánh MB+MC và CA
b) Tìm M trên d sao cho MB + MC bé nhất. Biết C là 1 điểm bất kì sao cho CB<CA
M thuộc d nên MA = MB. Vậy MB + MC = MA + MC. Trong tam giác MAC, ta có : MA + MC > AC. Vậy MB + MC > AC
Vì CB < CA nên C và B nằm trong cùng một nửa mặt phẳng bờ d. Do đó A và C nằm trong hai nửa mặt phẳng bờ d khác nhau. Do đó d cắt AC tại H.
Vậy khi M ≡≡ H thì : MB + MC = HB + HC = HA + HC
=> MB + MC = AC
Vậy ta có MB + MC ≥ AC
Khi M trùng với H thì HB + HC = AC.
Tức là MB + MC nhỏ nhất khi M ≡≡ H giao điểm của AC với d
Bài 3: Cho đoạn thẳng AB, gọi I là trung điểm của AB. Trên đường trung trực của đoạn thẳng AB lấy điểm M (M≠I).
a) Chứng minh tam giác MAB cân.
b) Kẻ IH vuông góc với MA, kẻ IK vuông góc với MB. Chứng minh IH = IK.
cho đoạn thẳng AB= 6cm. kẻ đường thẳng d là đường trung trực của đoạn thẳng AB, lấy điểm M thuộc đường thẳng d sao cho khoảng cách từ M đến đoạn thẳng AB=4cm. tính độ dài đoạn thẳng MA,MB
Cho đoạn thẳng AB.Đường trung trực của đoạn thẳng AB cắt AB tại I. Lấy điểm M bất kì nằm trên đường trung trực của đoạn thẳng AB.
a/ Chứng minh: AM=MB.
b/ Chứng minh: MI là tia phân giác của góc AMB.
c/ Biết : Góc AMB bằng \(^{ }\)\(110^o\) . Hãy tính số đo góc ngoài tại đỉnh A.
a: Ta có: M nằm trên đường trung trực của AB
nên MA=MB
b: Ta có: ΔMAB cân tại M
mà MI là đường trung trực
nên MI là đường phân giác
Đúng 1
Bình luận (1)
Cho đoạn thẳng AB. Gọi d là đường trung trực của AB. Trên đường thẳng d lấy điểm M bất kì. Trong mặt phẳng lấy điểm C sao cho BC< CA
,Tìm vị trí của M trên d sao cho MB+MC nhỏ nhất
Mấy pro giúp cái coi :>
M thuộc d nên MA = MB. Vậy MB + MC = MA + MC. Trong tam giác MAC, ta có : MA + MC > AC. Vậy MB + MC > AC
Vì CB < CA nên C và B nằm trong cùng một nửa mặt phẳng bờ d. Do đó A và C nằm trong hai nửa mặt phẳng bờ d khác nhau. Do đó d cắt AC tại H.
Khi M trùng với H thì HB + HC = AC.
Tức là MB + MC nhỏ nhất khi M ≡≡ H giao điểm của AC với d.
Trên đường trung trực của d của đoạn thẳng AB lấy điểm C bất kì.
a) Chứng minh: Tam giác HAC bằng tam giác BBC. Từ đó suy ra CA = CB ( H là giao điểm của D thuộc d )
b) Trên nửa mặt phẳng không chứa điểm C bờ AB lấy điểm D thuộc d. Chứng minh: Tam giác CAD bằng tam giác CBD.
Giải:
Vì d là đường trung trực của AB và cắt AB tại H
\(\Rightarrow AH=HB\) (*)
Xét \(\Delta HAC,\Delta HBC\) có:
AH = HB ( theo (*) )
\(\widehat{AHC}=\widehat{BHC}\left(=90^o\right)\)
CH: cạnh chung
\(\Rightarrow\Delta HAC=\Delta HBC\left(c-g-c\right)\)
\(\Rightarrow CA=CB\) ( hai cạnh tương ứng ) ( đpcm )
b) Vì \(\Delta HAC=\Delta HBC\)
\(\Rightarrow\widehat{C_1}=\widehat{C_2}\) ( góc tương ứng )
Xét \(\Delta CAD,\Delta CBD\) có:
\(CA=CB\)
\(\widehat{C_1}=\widehat{C_2}\)
CD: cạnh chung
\(\Rightarrow\Delta CAD=\Delta CBD\left(c-g-c\right)\)
Đúng 0
Bình luận (0)
Xin lỗi nhé, câu hỏi câu a là thế này:
Chứng minh tam giác HAC bằng tam giác HBC. Từ đó suy ra CA = CB ( H là giao điểm của d với AB)
Đúng 0
Bình luận (0)
cho đoạn thẳng AB gọi d là đương trung trực của AB trên đường thẳng d lấy điểm M bất kì trong mặt phẳng lấy C sao cho BC<Ca
so sánh MB +MC với CA
tìm vị trí của M trên d sao cho MB +MC nhỏ nhất
M thuộc d nên MA = MB. Vậy MB + MC = MA + MC. Trong tam giác MAC, ta có : MA + MC > AC. Vậy MB + MC > AC
Vì CB < CA nên C và B nằm trong cùng một nửa mặt phẳng bờ d. Do đó A và C nằm trong hai nửa mặt phẳng bờ d khác nhau. Do đó d cắt AC tại H.
Vậy khi M ≡≡ H thì : MB + MC = HB + HC = HA + HC
=> MB + MC = AC
Vậy ta có MB + MC ≥ AC
Khi M trùng với H thì HB + HC = AC.
Tức là MB + MC nhỏ nhất khi M ≡≡ H giao điểm của AC với d.
Cho đường tròn (O; R), đường thẳng d cắt (O ) tại C, D. Điểm M tùy ý trên đường thẳng d. Kẻ tiếp tuyến MA, MB với đường tròn (O). Gọi I là trung điểm của CD, H là trực tâm của tam giác MAB. 1. Chứng minh AB là trung trực của OH. 2. Khi M di động trên đường thẳng d.Chứng minh rằng AB luôn đi qua một điểm cố định. 3. Đường thẳng qua C vuông góc với OA cắt AB, AD lần lượt tại E, K. Chứng minh EC EKgiúp tớ phần 3 với
Đọc tiếp
Cho đường tròn (O; R), đường thẳng d cắt (O ) tại C, D. Điểm M tùy ý trên đường thẳng d. Kẻ tiếp tuyến MA, MB với đường tròn (O). Gọi I là trung điểm của CD, H là trực tâm của tam giác MAB.
1. Chứng minh AB là trung trực của OH.
2. Khi M di động trên đường thẳng d.Chứng minh rằng AB luôn đi qua một điểm
cố định.
3. Đường thẳng qua C vuông góc với OA cắt AB, AD lần lượt tại E, K.
Chứng minh EC = EK
giúp tớ phần 3 với
Cho đoạn thẳng AB có trung điểm O, d là đường trung trực của đoạn thẳng AB, điểm M thuộc d, M khác O (Hình 90).
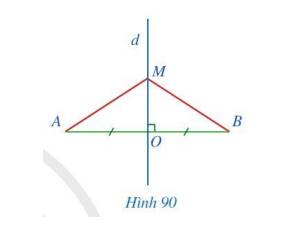
Chứng minh rằng:
a) \(\Delta MOA = \Delta MOB\);
b) MA = MB.
a) Ta có: d là đường trung trực của đoạn thẳng AB, điểm M thuộc d nên MO là đường trung trực của đoạn thẳng AB
\(\Rightarrow MO \bot AB \to \widehat {MOA} = \widehat {MOB} = 90^\circ \).
Xét tam giác MOA và tam giác MOB có:
OM chung;
\(\widehat {MOA} = \widehat {MOB} = 90^\circ \);
OA = OB (O là trung điểm của đoạn thẳng AB).
Vậy \(\Delta MOA = \Delta MOB\) (c.g.c)
b) \(\Delta MOA = \Delta MOB\) nên MA = MB ( 2 cạnh tương ứng)
Đúng 0
Bình luận (0)


















