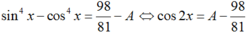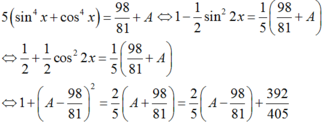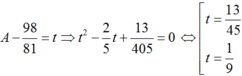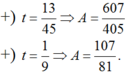Chọn D.

Ta có 

Đặt 

\(sin4x=-cos2x\\ \Leftrightarrow sin4x+cos2x=0\\ \Leftrightarrow2sin2x.cos2x+cos2x=0\\ \Leftrightarrow cos2x\left(2sin2x+1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}cos2x=0\\2sin2x+1=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}cos2x=\dfrac{\pi}{2}+k\pi\\sin2x=-\dfrac{1}{2}\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{4}+\dfrac{k\pi}{2}\\sin2x=sin\left(-\dfrac{\pi}{6}\right)\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{4}+\dfrac{k\pi}{2}\\x=-\dfrac{\pi}{12}+k\pi\\x=\dfrac{7\pi}{12}+k\pi\end{matrix}\right.\)

`HaNa♫D`

\(sin\dfrac{4x}{3}=-\dfrac{1}{3}\)

\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{3}{4}arcsin\left(-\dfrac{1}{3}\right)+\dfrac{k3\pi}{2}\\x=\dfrac{3\pi}{4}-\dfrac{3}{4}arcsin\left(-\dfrac{1}{3}\right)+\dfrac{k\pi}{2}\end{matrix}\right.\)

\(\Leftrightarrow2sinx+cos3x+sin2x-sin4x-1=0\)

\(\Leftrightarrow2sinx-1+cos3x-2cos3x.sinx=0\)

\(\Leftrightarrow2sinx-1-cos3x\left(2sinx-1\right)=0\)

\(\Leftrightarrow\left(2sinx-1\right)\left(1-cos3x\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}sinx=\frac{1}{2}\\cos3x=1\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=\frac{\pi}{6}+k2\pi\\x=\frac{5\pi}{6}+k2\pi\\x=\frac{k2\pi}{3}\end{matrix}\right.\)

ĐKXĐ: \(\left\{{}\begin{matrix}sinx< >0\\sin2x< >0\\sin4x< >0\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}x< >k\Omega\\2x< >k\Omega\\4x< >k\Omega\end{matrix}\right.\Leftrightarrow x\ne\dfrac{k\Omega}{4}\)

\(\dfrac{1}{sinx}+\dfrac{1}{sin2x}+\dfrac{1}{sin4x}=0\)

=>\(\dfrac{1}{sinx}+cotx+\dfrac{1}{sin2x}+cot2x+\dfrac{1}{sin4x}+cot4x=cotx+cot2x+cot4x\)

=>\(\dfrac{1+cosx}{sinx}+\dfrac{1+cos2x}{sin2x}+\dfrac{1+cos4x}{sin4x}=cotx+cot2x+cot4x\)

=>\(\dfrac{2\cdot cos^2\left(\dfrac{x}{2}\right)}{2\cdot sin\left(\dfrac{x}{2}\right)\cdot cos\left(\dfrac{x}{2}\right)}+\dfrac{2\cdot cos^2x}{2\cdot sinx\cdot cosx}+\dfrac{2\cdot cos^22x}{2\cdot sin2x\cdot cos2x}=cotx+cot2x+cot4x\)

=>\(\dfrac{cos\left(\dfrac{x}{2}\right)}{sin\left(\dfrac{x}{2}\right)}+\dfrac{cosx}{sinx}+\dfrac{cos2x}{sin2x}=cotx+cot2x+cot4x\)

=>\(cot\left(\dfrac{x}{2}\right)+cotx+cot2x=cotx+cot2x+cot4x\)

=>\(cot4x=cot\left(\dfrac{x}{2}\right)\)

=>\(\left\{{}\begin{matrix}4x=\dfrac{x}{2}+k\Omega\\4x< >k\Omega\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}\dfrac{7}{2}x=k\Omega\\x< >\dfrac{k\Omega}{4}\end{matrix}\right.\Leftrightarrow x=\dfrac{2}{7}k\Omega\)

\(\dfrac{1}{sinx}+\dfrac{1}{sin2x}+\dfrac{1}{sin4x}=0\)

\(\dfrac{1}{sinx}+cotx+\dfrac{1}{sin2x}+cot2x+\dfrac{1}{sin4x}+cot4x=cotx+cot2x+cot4x\)

\(\dfrac{1+cosx}{sinx}+\dfrac{1+cos2x}{sin2x}+\dfrac{1+cos4x}{sin4x}=cotx+cot2x+cot4x\)

\(\dfrac{2cos^2\dfrac{x}{2}}{2sin\dfrac{x}{2}.cos\dfrac{x}{2}}+\dfrac{2cos^2x}{2sinx.cosx}+\dfrac{2cos^22x}{2sin2x.cos2x}=cotx+cot2x+cot4x\)

\(\dfrac{cos\dfrac{x}{2}}{sin\dfrac{x}{2}}+\dfrac{cosx}{sinx}+\dfrac{cos2x}{sin2x}=cotx+cot2x+cot4x\)

\(cot\dfrac{x}{2}+cotx+cot2x=cotx+cot2x+cot4x\)

\(cot\dfrac{x}{2}=cot4x\)

\(\Rightarrow\dfrac{x}{2}=4x+k\text{π}\)

\(\Leftrightarrow x=-\dfrac{k2\text{π}}{7}\)

Đề là \(\sqrt{5}cos4x\) hay \(\sqrt{3}cos4x\) bạn?

Lời giải:

PT $\Leftrightarrow 2\sin 2x\cos 2x+2\cos 2x+4(\sin x+\cos x)=1+\cos ^22x-\sin ^22x=2\cos ^22x$

$\Leftrightarrow \sin 2x\cos 2x+\cos 2x+2(\sin x+\cos x)=\cos ^22x$

$\Leftrightarrow \cos 2x(\sin 2x+1-\cos 2x)+2(\sin x+\cos x)=0$

$\Leftrightarrow \cos 2x(2\sin x\cos x+2\sin ^2x)+2(\sin x+\cos x)=0$

$\Leftrightarrow \cos 2x\sin x(\cos x+\sin x)+(\sin x+\cos x)=0$

$\Leftrightarrow (\sin x+\cos x)(\cos 2x\sin x+1)=0$

Nếu $\sin x+\cos x=0$. Kết hợp $\sin ^2x+\cos ^2x=1$ suy ra $(\sin x, \cos x)=(\frac{1}{\sqrt{2}}; \frac{-1}{\sqrt{2}})$ và hoán vị

$\Rightarrow x=k\pi -\frac{\pi}{4}$ với $k$ nguyên.

Nếu $\cos 2x\sin x+1=0$

$\Leftrightarrow (1-2\sin ^2x)\sin x+1=0$

$\Leftrightarrow (1-\sin x)(2\sin ^2x+2\sin x+1)=0$

$\Rightarrow \sin x=1$

$\Rightarrow x=2k\pi +\frac{\pi}{2}$ với $k$ nguyên.

nguyễn thị hương giang 

mình trình bày chút, giờ mình ms onl

Cộng cả 2 vế với cot8x

\(\dfrac{1}{sin8x}+cot8x=\dfrac{1+cos8x}{sin8x}=\dfrac{2cos^24x}{2sin4x.cos4x}=cot4x\)

Rồi cot4x lại đi với \(\dfrac{1}{sin4x}\) tạo cot2x ư

........... cứ như thế phương trình sẽ trở thành 

\(cot\dfrac{x}{2}=cot8x\)