√x2-2x+2 =1
giải phương trình
giải phương trình:
11/x2 - 25/(x+5)2 = 1
giải giúp em với ạ!
ĐKXĐ: \(x\ne\left\{0;-5\right\}\)
\(\Leftrightarrow\dfrac{11}{x^2}-\left[1-\dfrac{10}{x+5}+\left(\dfrac{5}{x+5}\right)^2+\dfrac{10}{x+5}\right]=0\)
\(\Leftrightarrow\dfrac{11}{x^2}-\left[\left(1-\dfrac{5}{x+5}\right)^2+\dfrac{10}{x+5}\right]=0\)
\(\Leftrightarrow\dfrac{11}{x^2}-\dfrac{10}{x+5}-\left(\dfrac{x}{x+5}\right)^2=0\)
\(\Leftrightarrow\left(\dfrac{1}{x}-\dfrac{x}{x+5}\right)\left(\dfrac{11}{x}+\dfrac{x}{x+5}\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}\dfrac{1}{x}-\dfrac{x}{x+5}=0\\\dfrac{11}{x}+\dfrac{x}{x+5}=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x^2-x-5=0\\x^2+11x+55=0\end{matrix}\right.\)
\(\Leftrightarrow...\) (bấm máy)
1giải phương trình 9x4 +8x2-1=0
2 cho pt :x2 -(m-1)x-m2 +m-1=0
a) CMT phương trình luôn có 2 nghiệm phân biệt với x1,x2 với mọi m
1) \(9x^4+8x^2-1=0\)
\(\Leftrightarrow9x^4+9x^2-x^2-1=0\)
\(\Leftrightarrow9x^2\left(x^2+1\right)-\left(x^2+1\right)=0\)
\(\Leftrightarrow\left(x^2+1\right)\left(9x^2-1\right)=0\)
\(\Rightarrow9x^2-1=0\)
\(\Leftrightarrow x=\dfrac{\pm1}{3}\)
Vậy...
2) \(\Delta=\left(m-1\right)^2-4\left(-m^2+m-1\right)\) \(=5m^2-6m+5\)
Có: \(5m^2-6m+5=5\left(m^2-\dfrac{6}{5}m+\dfrac{9}{25}\right)+\dfrac{16}{5}\)
\(=5\left(m-\dfrac{3}{5}\right)^2+\dfrac{16}{5}\ge\dfrac{16}{5}>0\forall m\in R\)
\(\Rightarrow\Delta>0\forall m\in R\)
Vậy: PT luôn có 2 nghiệm phân biệt với mọi m.
d. x2−x−2x+1x2−x−2x+1=x2−3x+2x−1
Giải giùm m câu này mà ko dùng nhân chéo vs ![]()
1Giải các phương trình sau bằng cách đưa về phương trình tích:
a) 3x(2x – 3) = 5(3 – 2x)
b) (x2 + 1)(2x + 5) = (x – 1)(x2 + 1)
c) 3x3 = x2 + 3x - 1
d) x2 – 9x + 20 = 0
2Giải các phương trình sau bằng cách đưa về phương trình tích:
a) 3x(2x – 3) = 5(3 – 2x)
b) (x2 + 1)(2x + 5) = (x – 1)(x2 + 1)
c) 3x3 = x2 + 3x - 1
d) x2 – 9x + 20 = 0
a/ \(3x(2x-3)=5(3-2x) \Leftrightarrow 3x(2x-3)+5(2x-3)=0 \\\ \Leftrightarrow (2x-3)(3x+5)=0 \)
\(\Leftrightarrow\left[{}\begin{matrix}2x-3=0\\3x+5=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\frac{3}{2}\\x=-\frac{5}{3}\end{matrix}\right.\)
KL: .............
b/ \(\left(x^2+1\right)\left(2x+5\right)=\left(x-1\right)\left(x^2+1\right)\Leftrightarrow\left(x^2+1\right)\left(2x+5\right)-\left(x-1\right)\left(x^2+1\right)=0\)
\(\Leftrightarrow\left(x^2+1\right)\left(2x+5-x+1\right)=0\Leftrightarrow\left[{}\begin{matrix}x^2+1=0\\x+6=0\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x\in\varnothing\\x=-6\end{matrix}\right.\)
KL: .............
c/ \(3x^3=x^2+3x-1\Leftrightarrow3x^3-x^2-3x+1=0\Leftrightarrow x^2\left(3x-1\right)-\left(3x-1\right)=0\)
\(\Leftrightarrow\left(3x-1\right)\left(x^2-1\right)=0\Leftrightarrow\left[{}\begin{matrix}3x-1=0\\x^2-1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\frac{1}{3}\\x=1\\x=-1\end{matrix}\right.\)
KL: ..........
d/ \(x^2-9x+20=0\Leftrightarrow x^2-5x-4x+20=0\Leftrightarrow x\left(x-5\right)-4\left(x-5\right)=0\)
\(\Leftrightarrow\left(x-5\right)\left(x-4\right)=0\Leftrightarrow\left[{}\begin{matrix}x-5=0\\x-4=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=5\\x=4\end{matrix}\right.\)
KL: .............
\(a,3x\left(2x-3\right)=5\left(3-2x\right)\Leftrightarrow6x^2-9x=15-10x\Leftrightarrow6x^2-9x-15+10x=0\Leftrightarrow6x^2+x-15=0\Leftrightarrow\left(3x+5\right)\left(2x-3\right)=0\)
\(\left(3x+5\right)\left(2x-3\right)=0\)
\(\left[{}\begin{matrix}x=-\frac{5}{3}\\x=\frac{3}{2}\end{matrix}\right.\)
1 Trong các phương trình sau, phương trình nào vô nghiệm:
A. x2 – 2x + 2 = 0 B. x2 – 2x + 1 = 0
C. x2 – 2x = 0 D. 2x – 10 = 2x – 10
2 Phương trình nào sau đây có 1 nghiệm :
A. x2 – 3 x = 0 B. 2x + 1 =1 +2x
C. x ( x – 1 ) = 0 D. (x + 2)(x2 + 1) = 0
cho phương trình \(x^2-2\left(m-1\right)x+m-5=0\)
1giải phương trình đã cho với m=2
2 tìm m để phương trình có hai nghiệm \(x_1,x_2\).tìm m để biểu thức \(P=\left|x_1-x_2\right|\)đạt giá trị nhỏ nhất
1.Thế `m=2` vào pt, ta được:
\(x^2-2\left(2-1\right)x+2-5=0\)
\(\Leftrightarrow x^2-2x-3=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-1\\x=3\end{matrix}\right.\) ( Vi-ét )
2.
Theo hệ thức Vi-ét, ta có: \(\left\{{}\begin{matrix}x_1+x_2=2\left(m-1\right)\\x_1x_2=m-5\end{matrix}\right.\)
\(P=\left|x_1-x_2\right|\)
\(\Leftrightarrow P^2=\left(x_1+x_2\right)^2-4x_1x_2\)
\(\Leftrightarrow P^2=\left[2\left(m-1\right)\right]^2-4\left(m-5\right)\)
\(\Leftrightarrow P^2=4\left(m-1\right)^2-4\left(m-5\right)\)
\(\Leftrightarrow P^2=4m^2-8m+4-4m+20\)
\(\Leftrightarrow P^2=4m^2-12m+24\)
\(\Leftrightarrow P^2=\left(2m-3\right)^2+15\)
\(P^2\ge15\)
mà \(P\ge0\)
\(\Rightarrow Min_P=\sqrt{15}\)
Dấu "=" xảy ra khi \(2m-3=0\) \(\Leftrightarrow m=\dfrac{3}{2}\)
Vậy \(Min_P=\sqrt{15}\) khi \(m=\dfrac{3}{2}\)
\(x^2-2(m-1)x+m-5=0\ \ (1) \\1)Thay\ m=2\ vào\ (1)\ ta\ có: \\x^2-2(2-1)x+2-5=0 \\<=>x^2-2x-3=0<=>(x+1)(x-3)=0<=>x=-1\ hoặc\ x=3 \\2)\triangle'=[-(m-1)]^2-1.(m-5)=m^2-3m+6>0\ với\ mọi\ m \\->Phương\ trình\ (1)\ luôn\ có\ 2\ nghiệm\ phân\ biệt\ với\ mọi\ m. \\Theo\ hệ\ thức\ Vi-ét\ ta\ có: \\x_1+x_2=2(m-1);x_1x_2=m-5 \)
\(Ta\ có: P^2=x_1^2-2x_1x_2+x_2^2=(x_1+x_2)^2-4x_1x_2 \\=[2(m-1)]^2-4(m-5)=4(m-\dfrac{3}{2})^2+15\ge15 \\->P\ge\sqrt{15} \\Đẳng\ thức\ xảy\ ra\ khi\ m=\dfrac{3}{2}. \\Vậy\ P\ nhỏ\ nhất\ bằng\ \sqrt{15}\ (khi\ m=\dfrac{3}{2}).\)
Rút gọn biểu thức :
N=\(\dfrac{\sqrt{x}+1}{\sqrt{x}-1}-\dfrac{3\sqrt{x}}{x-\sqrt{x}}\) với x>0,x\(\ne\)1
Giải hệ phương trình:
\(\left\{{}\begin{matrix}x+3y=9\\2x-5y=-4\end{matrix}\right.\)
a) Ta có: \(N=\dfrac{\sqrt{x}+1}{\sqrt{x}-1}-\dfrac{3\sqrt{x}}{x-\sqrt{x}}\)
\(=\dfrac{\sqrt{x}+1-3}{\sqrt{x}-1}\)
\(=\dfrac{\sqrt{x}-2}{\sqrt{x}-1}\)
b) Ta có: \(\left\{{}\begin{matrix}x+3y=9\\2x-5y=-4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2x+6y=18\\2x-5y=-4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}11y=22\\x+3y=9\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}y=2\\x=9-3y=9-3\cdot2=3\end{matrix}\right.\)
Giải phương trình bằng cách đưa về phương trình tích:
(x2 + 2x – 5)2 = (x2 – x + 5)2
(x2 + 2x – 5)2 = (x2 – x + 5)2
⇔ (x2 + 2x – 5)2 – (x2 – x + 5)2 = 0
⇔ [(x2 + 2x – 5) – (x2 – x + 5)].[(x2 + 2x – 5) + (x2 – x + 5)] = 0
⇔ (3x – 10)(2x2 + x ) = 0
⇔ (3x-10).x.(2x+1)=0
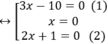
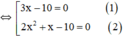
+ Giải (1): 3x – 10 = 0 ⇔ 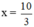
+ Giải (2):
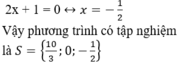
cho phương trình x2-2x+m-1=0 . Tìm m để phương trình có hai nghiệm x1 , x2 thỏa mãn 2x1(x1-x2)+3=7m+(x2+2)2
Δ=(-2)^2-4(m-1)=4-4m+4=8-4m
Để phương trình có hai nghiệm thì 8-4m>=0
=>m<=2
x1+x2=2; x1x2=m-1
=>x1=2-x2
=>x1+1=3-x2
x1^2+x2^2=(x1+x2)^2-2x1x2=2^2-2(m-1)=4-2m+2=6-2m
=>x1^2=6-2m-x2^2
2x1(x1-x2)+3=7m+(x2+2)^2
=>2x1^2-2x1x2+3=7m+x2^2+2x2+4
=>2(6-2m-x2^2)-2x1x2+3-7m-x2^2-2x2-4=0
=>2(6-2m-x2^2)-2x2(3-x2)-7m-1=0
=>12-4m-2x2^2-6x2-2x2^2-7m-1=0
=>-4x2^2-6x2-11m+11=0
=>4x2^2+6x2+11m-11=0(1)
Để phương trình (1) có nghiệm thì 6^2-4*4*(11m-11)>=0
=>36-16(11m-11)>=0
=>16(11m-11)<=36
=>11m-11<=9/4
=>11m<=53/4
=>m<=53/44
giải bất phương trình \(\dfrac{2-x}{x}\)≥1
A. x≤1 B. 0<x≤1 C. x>1 D. 0<x<1
giải chi tiết giúp mik
`[2-x]/x >= 1`
`<=>[2-x-x]/x >= 0`
`<=>[2-2x]/x >= 0`
`<=>0 < x <= 1`
`->\bb B`