
Những câu hỏi liên quan
Cho tam giác ABC, các đường cao BD, CE cắt nhau tại H. Đường vuông góc với AB tại B và đường vuông góc với AC tại C cắt nhau ở K. Gọi M là trung điểm BC.
a/ chứng minh tam giác ADB đồng dạng tam giác AEC
b/ chứng minh HE. HC = HD. HB
Cho tam giác ABC, các đường cao BD, CE cắt nhau tại H. Đường vuông góc với AB tại B và đường vuông góc với AC tại C cắt nhau ở K. Gọi M là trung điểm BC.
a/ chứng minh tam giác ADB đồng dạng tam giác AEC
b/ chứng minh HE. HC = HD. HB
a, Xét tam giác ADB và tam giác AEC có:
^A chung
^AEC = ^ADB
\(\Rightarrow\) ADB đồng dạng AEC
b,Xét tam giác HEB và tam giác HDC có:
^EHB = ^DHC
^HEB = ^HDC
\(\Rightarrow\) tam giác HEB đồng dạng tam giác HDC
\(\Rightarrow\) HE.HC = HD.HB
Đúng 2
Bình luận (0)
Cho tam giác ABC, các đường cao BD, CE cắt nhau tại H. Đường vuông góc với AB tại B và đường vuông góc với AC tại C cắt nhau ở K. Gọi M là trung điểm BC.
a/ chứng minh tam giác ADB đồng dạng tam giác AEC
b/ chứng minh HE. HC = HD. HB
a) xét tam giác ADB và AEC có:
góc A chung
góc ADB= góc AEC (=90 độ)
=> ADB đồng dạng vs AEC (g.g)
b) xét tam giác EHB và tam giác DHC có:
EHB= DHC (2 góc đối đỉnh)
HEB- HDC (=90độ)
=> EHB =DHC (g.g)
=> HE/HB = HD/HC
=> HE.HC=HD.HB
Đúng 0
Bình luận (0)
a) xét tam giác ADB và AEC có:
góc A chung
góc ADB= góc AEC (=90 độ)
=> ADB đồng dạng vs AEC (g.g)
b) xét tam giác EHB và tam giác DHC có:
EHB= DHC (2 góc đối đỉnh)
HEB=HDC (=90độ)
=> EHB đồng dạng DHC (g.g)
=> HE/HB = HD/HC
=> HE.HC=HD.HB
Đúng 0
Bình luận (0)
Cho tam giác ABC, các đường cao BD, CE cắt nhau tại H. Đường vuông góc với AB tại B và đường vuông góc với AC cắt nhau tại K. Gọi M là trung điểm của BC.
a) Chứng minh tam giác ADB đồng dạng với tam giác AEC
b) Chứng minh HE.HC = HD.HB
c) Chứng minh H, K, M thẳng hàng
d) Tam giác AEC phải có điều kiện gì thì tứ giác BHCK là hình thoi? Là hình chữ nhật?
a) Xét ΔABD vuông tại D và ΔACE vuông tại E có
\(\widehat{EAC}\) chung
Do đó: ΔABD\(\sim\)ΔACE(g-g)
b) Xét ΔHEB vuông tại E và ΔHDC vuông tại D có
\(\widehat{EHB}=\widehat{DHC}\)(hai góc đối đỉnh)
Do đó: ΔHEB\(\sim\)ΔHDC(g-g)
Suy ra: \(\dfrac{HE}{HD}=\dfrac{HB}{HC}\)
hay \(HE\cdot HC=HB\cdot HD\)
Đúng 2
Bình luận (0)
Cho tam giác ABC các đường cao BD,CE cắt nhau tại H. Đường vuông góc với AB tại B và đường vuông góc với AC tại C cắt nhau ở K. Gọi MN là trung điểm của BC. a) CM: tam giác ADB đồng dạng với tam giác AEC ( biết rồi ) b) CM: HE.HC HD.HB (biết rồi) c) CM: H,M,K thẳng hàng ( chưa biết) d) tam giác ABC phải có điều kiện gì để tứ giác BACK là hình thoi ? là hình chữ nhật ? ( chưa biết ) MÌNH CHỈ CẦN Ý c Và d thôi ạ !
Đọc tiếp
Cho tam giác ABC các đường cao BD,CE cắt nhau tại H. Đường vuông góc với AB tại B và đường vuông góc với AC tại C cắt nhau ở K. Gọi MN là trung điểm của BC. a) CM: tam giác ADB đồng dạng với tam giác AEC ( biết rồi ) b) CM: HE.HC = HD.HB (biết rồi) c) CM: H,M,K thẳng hàng ( chưa biết) d) tam giác ABC phải có điều kiện gì để tứ giác BACK là hình thoi ? là hình chữ nhật ? ( chưa biết ) MÌNH CHỈ CẦN Ý c Và d thôi ạ !
c: Xét tứ giác BHCK có
BH//CK
BK//CH
=>BHCK là hbh
=>M là trung điểm của HK
=>H,M,K thẳng hàng
d: BACK là hình thoi
=>M là trung điểm của AK và AK vuông góc BC
=>A,H,M thẳng hàng
=>ΔABC cân tại A
=>AB=AC
Đúng 1
Bình luận (0)
tham khảo
a.Ta có BK//CH(⊥AB),CK//BH(⊥AC)BK//CH(⊥AB),CK//BH(⊥AC)
→BHCK→BHCK là hình bình hành
b.Vì BHCKBHCK là hình bình hành
→HK∩BC→HK∩BC tại trung điểm mỗi đường
Do MM là trung điểm BCBC
→M→M là trung điểm HKHK
→H,M,K→H,M,K thẳng hàng
c.Ta có O,MO,M là trung điểm AK,HKAK,HK
→OM→OM là đường trung bình ΔAHKΔAHK
→OM//AH→OM//AH
Do BD∩CE=H→HBD∩CE=H→H là trực tâm ΔABC→AH⊥BCΔABC→AH⊥BC
→OM⊥BC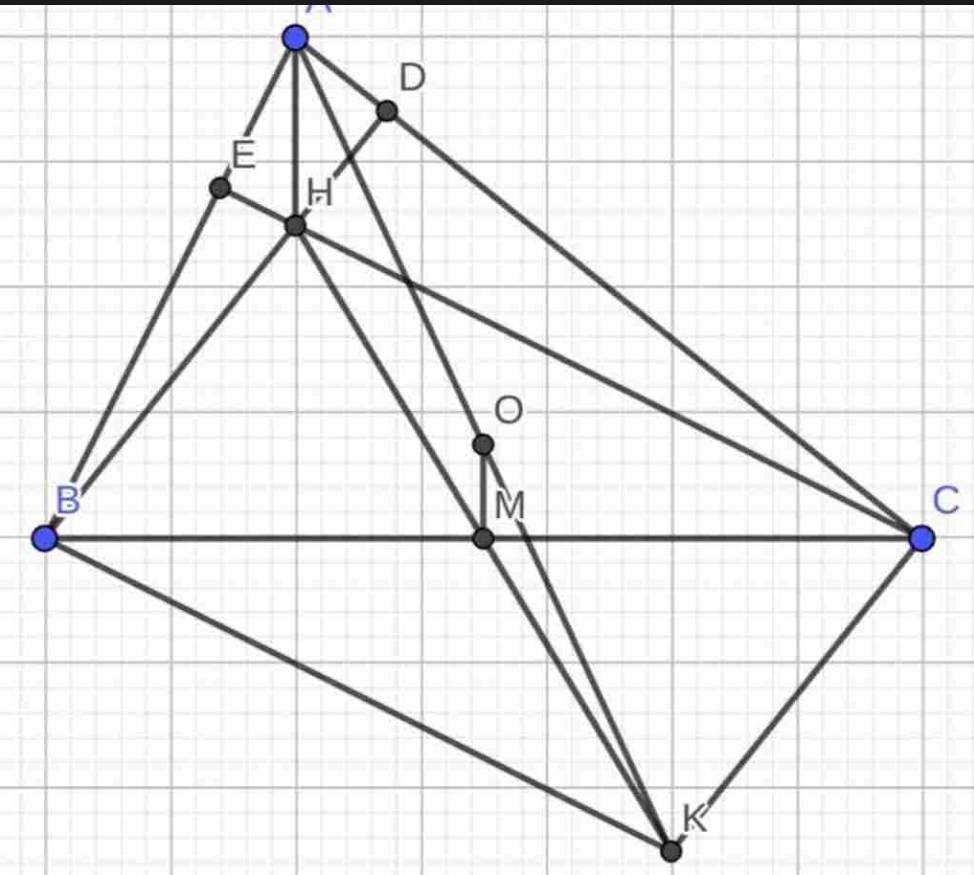
Đúng 1
Bình luận (0)
Cho tam giác ABC, các đường cao BD, CE cắt nhau tại H. Đường vuông góc với AB tại B và đường vuông góc với AC tại C cắt nhau ở K. Gọi M là trung điểm BC.
a/ chứng minh tam giác ADB đồng dạng tam giác AEC
b/ chứng minh HE. HC = HD. HB
c/ chứng minh H, K , M thẳng hàng
chủ yếu câu c giúp giùm mình nha
c) Ta có AB vuông góc BK; AB vuông góc CH => BK//CH
tương tự BH//CK => tứ giác BHCK là hình bình hành mà M là trung điểm BC => M là trugn điểm HK => H,M,K thẳng hàng
Đúng 1
Bình luận (0)
b)xét tam giác HEB và tam giác HDC có:
{góc HEB =góc HDC(=90 độ)
góc HEB=góc HDC(đối đỉnh)
=>tam giác HEB~Tam giác HDC(g.g)
=>HE/HD=HB/HC<=>HE.HC=HD.HB
c)ta có BD vuông AC và CK vuông AC=>BD // CK,BH//CK
ta lại có CE vuông AB và BK vuông AB=>CE//BK,CH//Bk
mà tứ giác BHCK có BH//CK và CH//BK=>BHCK là hbh(dhnb)
mà M là trung điểm của đường chéo BC
=>M cũng là trung điểm của đường chéo HK
=>H,M,K thẳng hàng.
ai biết giải dùm mình câu này với
d)tam giác ABC phải có điều kiện dì thì tứ giác BHCK là hình thoi?hình chữ nhật?
giúp mình với ạ
Đúng 0
Bình luận (0)
cho tam giác abc, các đường cao bd, ce cắt nhau tại h. đường vuông góc với ab tại b và đường vuông góc ac tại c cắt nhau ở k. gọi m là trung điểm của bc
a, cm tam giác adb đồng dạng tam giác aec
b, cm he.hc=hd.hb
c, cm h, k, m, thẳng hàng
d, tam giác abc phải có điều kiện gì thì tam giác bhck là hình thoi? hình chữ nhật?
a) Xét ΔADB vuông tại D và ΔAEC vuông tại E có
\(\widehat{EAC}\) chung
Do đó: ΔADB\(\sim\)ΔAEC(g-g)
Đúng 0
Bình luận (0)
cho tam giác ABC nhọn , các đường cao BD và CE cắt nhau tại H . Đường vuông góc AB tại B và đường vuông góc với AC tại C cắt nhau tại K . Gọi M là trung điểm của BC . Chứng minh
a , Chứng minh ADB∼ΔAEC và ΔAED ~ΔACB
d, AH cắt BC tại O . Chứng minh : BE . BA + CD . CA BC2
g, cho góc ACB 45o , gọi P là trung điểm của DC . Từ D kẻ đường thẳng vuông góc với BP tại I và cắt CK tại N . Tìm tỉ số diện tích của tứ giác CPIN và diện tích tam giác DCN
h, tam giác ABC có điềm kiện gì thì tứ giác BHCK...
Đọc tiếp
cho tam giác ABC nhọn , các đường cao BD và CE cắt nhau tại H . Đường vuông góc AB tại B và đường vuông góc với AC tại C cắt nhau tại K . Gọi M là trung điểm của BC . Chứng minh
a , Chứng minh ADB∼ΔAEC và ΔAED ~ΔACB
d, AH cắt BC tại O . Chứng minh : BE . BA + CD . CA = BC2
g, cho góc ACB = 45o , gọi P là trung điểm của DC . Từ D kẻ đường thẳng vuông góc với BP tại I và cắt CK tại N . Tìm tỉ số diện tích của tứ giác CPIN và diện tích tam giác DCN
h, tam giác ABC có điềm kiện gì thì tứ giác BHCK là hình thoi ? Hình chữ nhật ?
cho tam giác abc các đường cao bd, ce cắt nhau tại h. đường vuông góc với ab tại b và đường vuông góc với ac tại c cắt nhau ở k gọi m là trung điểm của bc
chứng minh tam giác adb đồng dạng với tam giác aec
chứng minh he nhân hc= hd nhân hb
chứng minh hs, k, m thẳng hàng
tam giác abc phải có điều kiện gì thì tứ giác bhck là hình thoi ? hình chữ nhật?

















