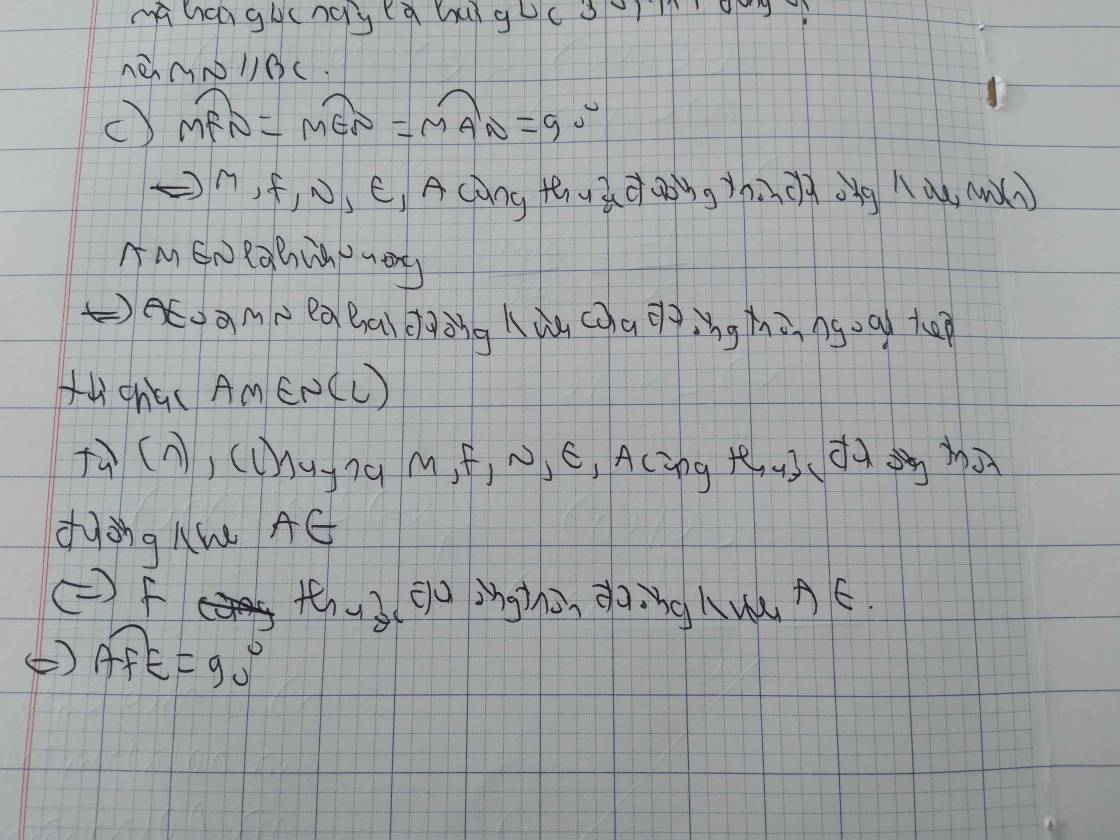Cho tam giác ABC vuông tại A. Lấy điểm M bất kì trên cạnh BC. Gọi E, F lần lượt là điểm đối
xứng với M qua AB và AC. Chứng minh A là trung điểm của EF.

Những câu hỏi liên quan
Cho tam giác vuông ABC (A = 90°). Lấy M bất kì trên cạnh BC. Gọi E, F lần lượt là các điểm đối xứng với M qua AB và AC. Gọi I, K lần lượt là giao điểm của MẸ với AB và MF với AC. Chứng minh:
a) MIAK là hình chữ nhật.
b) A là trung điểm của EF.
a: M đối xứng E qua AB
=>AB là đường trung trực của ME
=>AB\(\perp\)ME tại I và I là trung điểm của ME
Ta có: M đối xứng F qua AC
=>AC là đường trung trực của MF
=>AC\(\perp\)MF tại K và K là trung điểm của MF
Xét tứ giác AIMK có
\(\widehat{AIM}=\widehat{AKM}=\widehat{KAI}=90^0\)
=>AIMK là hình chữ nhật
b: Ta có: AKMI là hình chữ nhật
=>AK//MI và AK=MI; KM//AI và KM=AI
Ta có: MI//AK
I\(\in\)ME
Do đó: IE//AK
Ta có: AK=IM
IM=IE
Do đó: AK=IE
Ta có: AI=MK
MK=KF
Do đó: AI=KF
Ta có: AI//MK
K\(\in\)MF
Do đó: AI//KF
Xét tứ giác AKIE có
AK//IE
AK=IE
Do đó: AKIE là hình bình hành
=>KI//AE và KI=AE
Xét tứ giác AIKF có
AI//KF
AI=KF
Do đó: AIKF là hình bình hành
=>KI//AF và KI=AF
Ta có: KI//AF
KI//AE
AE,AF có điểm chung là A
Do đó: E,A,F thẳng hàng
Ta có: KI=AE
KI=AF
Do đó: AE=AF
mà E,A,F thẳng hàng
nên A là trung điểm của EF
Đúng 1
Bình luận (0)
Cho tam giác vuông ABC( A ^ = 90°). Lấy M bất kì trên cạnh Gọi E, F lần lượt là các điếm đối xứng với M qua AB và AC. Chứng minh: A là trung điểm của EF.
cho tam giác vuông abc (góc a= 90 độ ) lấy m bất kì trên cạnh bc gọi e,f làn lượt là các điểm đối xứng với m qua ab và ac chứng minh a là trung điểm của ef
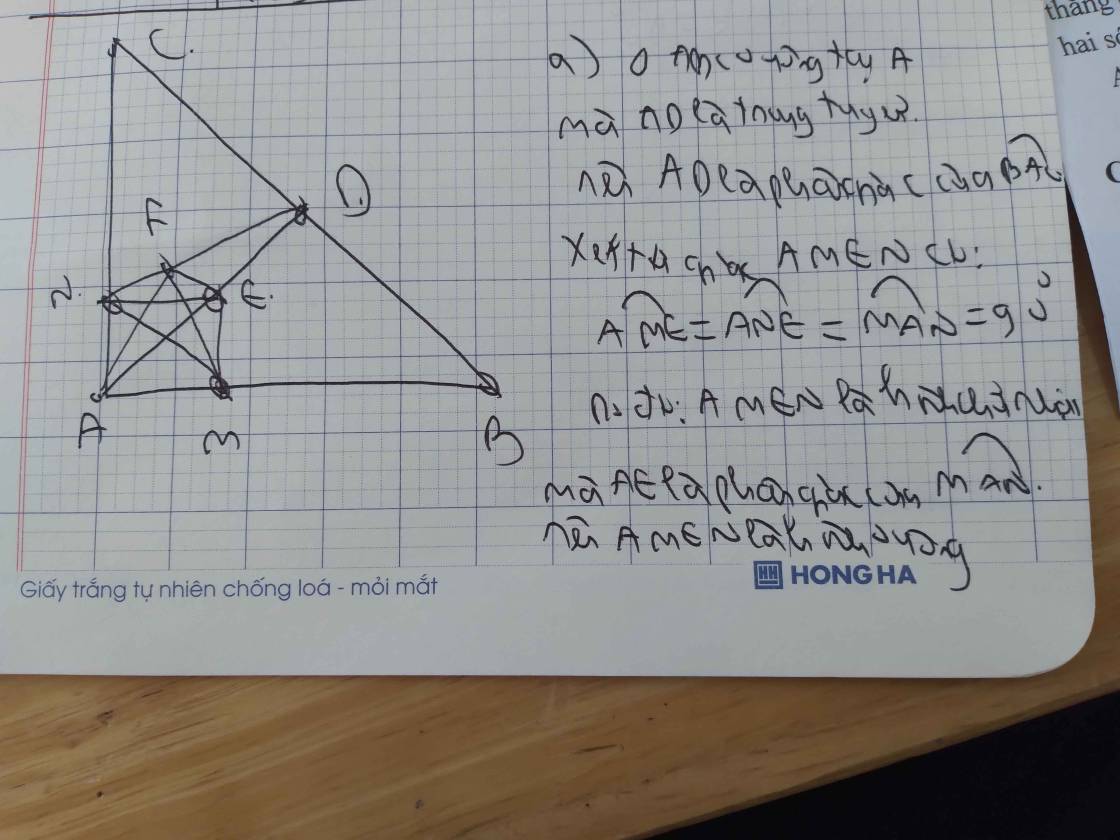
Cho tam giác ABC vuông cân tại A . Gọi D là trung điểm của BC. Trên đoạn AD lấy điểm E bất kì ( E khác A và D ). Qua E kẻ các đường vuông góc với AB AC , lần lượt tại M N, .
a) Chứng minh tứ giác AMEN là hình vuông.
b) Chứng minh MN BC / / .
c) Qua M kẻ đường thẳng vuông góc với DN tại F . Chứng minh AFE = 90 . d) Chứng minh B E F , , thẳng hàng.
Cho tam giác ABC vuông cân tại A . Gọi D là trung điểm của BC. Trên đoạn AD lấy điểm E bất kì ( E khác A và D ). Qua E kẻ các đường vuông góc với AB AC , lần lượt tại M N, .
a) Chứng minh tứ giác AMEN là hình vuông.
b) Chứng minh MN BC / / .
c) Qua M kẻ đường thẳng vuông góc với DN tại F . Chứng minh AFE = 90 . d) Chứng minh B E F , , thẳng hàng.
a: Xét tứ giác AMEN có
\(\widehat{AME}=\widehat{ANE}=\widehat{NAM}=90^0\)
Do đó: AMEN là hình chữ nhật
mà AE là tia phân giác
nen AMEN là hình vuông
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông cân tại A . Gọi D là trung điểm của BC. Trên đoạn AD lấy điểm E bất kì ( E khác A và D ). Qua E kẻ các đường vuông góc với AB AC , lần lượt tại M N, .
a) Chứng minh tứ giác AMEN là hình vuông.
b) Chứng minh MN BC / / .
c) Qua M kẻ đường thẳng vuông góc với DN tại F . Chứng minh AFE = 90 . d) Chứng minh B E F , , thẳng hàng.
Cho tam giác ABC vuông cân tại A . Gọi D là trung điểm của BC. Trên đoạn AD lấy điểm E bất kì ( E khác A và D ). Qua E kẻ các đường vuông góc với AB AC , lần lượt tại M N, .
a) Chứng minh tứ giác AMEN là hình vuông.
b) Chứng minh MN BC / / .
c) Qua M kẻ đường thẳng vuông góc với DN tại F . Chứng minh AFE = 90 . d) Chứng minh B E F , , thẳng hàng.
a: ΔABC cân tại A
mà AD là đường trung tuyến
nên AD là tia phân giác của \(\widehat{BAC}\)
Xét tứ giác AMEN có
\(\widehat{AME}=\widehat{ANE}=\widehat{MAN}=90^0\)
=>AMEN là hình chữ nhật
Hình chữ nhật AMEN có AE là phân giác của \(\widehat{MAN}\)
nên AMEN là hình vuông
b: AMEN là hình vuông
=>\(\widehat{AMN}=45^0\)
=>\(\widehat{AMN}=\widehat{ABC}\)
mà hai góc này là hai góc ở vị trí đồng vị
nênMN//BC
c: Gọi O là giao điểm của AE và MN
AMEN là hình vuông
=>AE cắt MN tại trung điểm của mỗi đường và AE=MN
=>O là trung điểm chung của AE và MN và AE=MN
=>\(OA=OE=OM=ON=\dfrac{MN}{2}=\dfrac{AE}{2}\)
ΔMFN vuông tại F
mà FO là đường trung tuyến
nên \(FO=\dfrac{MN}{2}=\dfrac{AE}{2}\)
Xét ΔAFE có
FO là đường trung tuyến
\(FO=\dfrac{AE}{2}\)
Do đó: ΔAFE vuông tại F
=>\(\widehat{AFE}=90^0\)
Đúng 2
Bình luận (0)
Cho tam giác ABC vuông tại A có D là trung điểm của BC. Trên AD lấy điểm M bất kì, Gọi E và F là hình chiếu của M trên AB, AC.
1) Chứng minh EF//BC
2) Kẻ EN vuông góc với FD
a)Tính góc ANM
b) Chứng minh NE là phân giác của góc ANM
3) Chứng minh 3 điểm B, M, N thẳng hàng
Cho ABC vuông tại A. Lấy M bất kì trên cạnh BC . Gọi E,F lần lượt là các điểm đối xứng với M qua AB,AC.
a) Chứng minh A, E, F thẳng hàng.
b) Chứng minh A là trung điểm của EF.
làm giusp em vs ạ em cảm ơn.
cho tam giác ABC vuông tại A. lấy điểm M bất kì trên cạnh AB(M khác A và B),từ M vẽ đg thẳng vuông góc với BC tại N
a)chứng minh BMN đồng dạng tam giác BCA
b) chứng minh BM×BA=BN×BC
c)gọi EF lần lượt là trung điểm của AN và CN. chứng minhh góc ABE = góc CBF
a: Xét ΔBMN vuông tại N và ΔBCA vuông tại A có
góc B chung
=>ΔBMN đồng dạng với ΔBCA
b: ΔBMN đồng dạng với ΔBCA
=>BM/BC=BN/BA
=>BM*BA=BN*BC
Đúng 0
Bình luận (0)