`a, x^2-10x+25=0`

`<=>x^2 -2.x.5+5^2=0`

`<=>(x-5)^2=0`

`<=>x-5=0`

`<=>x=5`

__

`x^2 -8x+16=0`

`<=> x^2 - 2.x.4+4^2=0`

`<=>(x-4)^2=0`

`<=>x-4=0`

`<=>x=4`

__

`x^2-49=0`

`<=>x^2 - 7^2=0`

`<=>(x-7)(x+7)=0`

`<=>x-7=0` hoặc `x+7=0`

`<=> x=7` hoặc `x=-7`

__

`4x^2-25=0`

`<=> (2x)^2 -5^2=0`

`<=>(2x-5)(2x+5)=0`

`<=>2x-5=0` hoặc `2x+5=0`

`<=> 2x=5` hoặc `2x=-5`

`<=>x=5/2` hoặc `x=-5/2`

a: =>(x-5)^2=0

=>x-5=0

=>x=5

b: =>(x-4)^2=0

=>x-4=0

=>x=4

c: =>(x-7)(x+7)=0

=>x-7=0 hoặc x+7=0

=>x=7 hoặc x=-7

d: =>(2x-5)(2x+5)=0

=>2x-5=0 hoặc 2x+5=0

=>x=5/2 hoặc x=-5/2

a) Thực hiện rút gọn VT = -2x – 64

Giải phương trình -2x – 64 = 0 thu được x = -32.

b) Thực hiện rút gọn VT = -62 x +12

Giải phương trình -62x + 12 = -50 thu được x = 1.

b: \(\Leftrightarrow x^4-4x^2+2x^2-8=0\)

\(\Leftrightarrow x+2=0\)

hay x=-2

\(a)\left(2x+5\right)\left(2x-7\right)-\left(-4x-3\right)^2=16\\ \Leftrightarrow4x^2-14x+10x-35-\left(16x^2+24x-9\right)=16\\ \Leftrightarrow-12x^2-28x-44=16\\ \Leftrightarrow-12x^2-28x-60=0\\ \Leftrightarrow3x^2+7x+15=0\\ \Delta=b^2-4ac=7^2-4.3.15=-131< 0\)

Vậy phương trình vô nghiệm

\( b)(8x^2 + 3)(8x^2 - 3) - (8x^2 - 1)^2 = 22\)

\(\Leftrightarrow64x^4-9-\left(64x^4-16x^2+1\right)=22\\ \Leftrightarrow-10+16x^2=22\\ \Leftrightarrow16x^2=32\\ \Leftrightarrow x^2=2\\ \Leftrightarrow x=\pm\sqrt{2}\)

Vậy \(x=\sqrt{2},x=-\sqrt{2}\)

\(c)49x^2+14x+1=0\\ \Leftrightarrow\left(7x+1\right)^2=0\\ \Leftrightarrow7x+1=0\\ \Leftrightarrow7x=-1\)

\(\Leftrightarrow\)\(x=-\dfrac{1}{7}\)

Vậy \(x=-\dfrac{1}{7}\)

\(\Leftrightarrow\)\(x=-\dfrac{1}{7}\)

a) \(2{x^2} + 3x + 1 \ge 0\)

Tam thức bậc hai \(f\left( x \right) = 2{x^2} + 3x + 1\) có 2 nghiệm phân biệt \(x =  - 1,x = \frac{{ - 1}}{2}\)

hệ số \(a = 2 > 0\)

Ta có bảng xét dấu f(x) như sau:

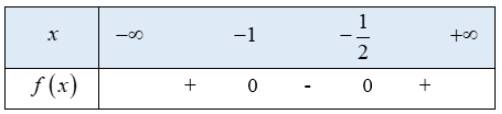
Từ bảng xét dấu ta thấy \(f\left( x \right) \ge 0 \Leftrightarrow \left[ \begin{array}{l}x \le  - 1\\x \ge  - \frac{1}{2}\end{array} \right.\)

Vậy tập nghiệm của bất phương trình là \(\left( { - \infty ; - 1} \right] \cup \left[ { - \frac{1}{2}; + \infty } \right)\)

b) \( - 3{x^2} + x + 1 > 0\)

Tam thức bậc hai \(f\left( x \right) =  - 3{x^2} + x + 1\) có 2 nghiệm phân biệt \(x = \frac{{1 - \sqrt {13} }}{6},x = \frac{{1 + \sqrt {13} }}{6}\)

Hệ số \(a =  - 3 < 0\)

Ta có bảng xét dấu f(x) như sau:

Từ bảng xét dấu ta thấy \(f\left( x \right) > 0\)\( \Leftrightarrow \frac{{1 - \sqrt {13} }}{6} < x < \frac{{1 + \sqrt {13} }}{6}\)

Vậy tập nghiệm của bất phương trình là \(\left( {\frac{{1 - \sqrt {13} }}{6};\frac{{1 + \sqrt {13} }}{6}} \right)\)

c) \(4{x^2} + 4x + 1 \ge 0\)

Tam thức bậc hai \(f\left( x \right) = 4{x^2} + 4x + 1\) có nghiệm duy nhất \(x = \frac{{ - 1}}{2}\)

hệ số \(a = 4 > 0\)

Ta có bảng xét dấu f(x) như sau:

Từ bảng xét dấu ta thấy \(f\left( x \right) \ge 0 \Leftrightarrow x \in \mathbb{R}\)

Vậy tập nghiệm của bất phương trình là \(\mathbb{R}\)

d) \( - 16{x^2} + 8x - 1 < 0\)

Tam thức bậc hai \(f\left( x \right) =  - 16{x^2} + 8x - 1\) có nghiệm duy nhất \(x = \frac{1}{4}\)

hệ số \(a =  - 16 < 0\)

Ta có bảng xét dấu f(x) như sau:

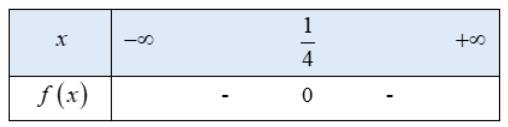
Từ bảng xét dấu ta thấy \(f\left( x \right) < 0 \Leftrightarrow x \ne \frac{1}{4}\)

Vậy tập nghiệm của bất phương trình là \(\mathbb{R}\backslash \left\{ {\frac{1}{4}} \right\}\)

e) \(2{x^2} + x + 3 < 0\)

Ta có \(\Delta  = {1^2} - 4.2.3 =  - 23 < 0\) và có \(a = 2 > 0\)

Sử dụng định lí về dấu của tam thức bậc hai, ta thấy tập hợp những giá trị của x sao cho \(2{x^2} + x + 3\) mang dấu “-” là \(\emptyset \)

Vậy tập nghiệm của bất phương trình \(2{x^2} + x + 3 < 0\) là \(\emptyset \)

g) \( - 3{x^2} + 4x - 5 < 0\)

Tam thức bậc hai \(f\left( x \right) =  - 3{x^2} + 4x - 5\) có \(\Delta ' = {2^2} - \left( { - 3} \right).\left( { - 5} \right) =  - 11 < 0\) và có \(a =  - 3 < 0\)

Sử dụng định lí về dấu của tam thức bậc hai, ta thấy tập hợp những giá trị của x sao cho \( - 3{x^2} + 4x - 5\) mang dấu “-” là \(\mathbb{R}\)

Vậy tập nghiệm của bất phương trình \( - 3{x^2} + 4x - 5 < 0\) là \(\mathbb{R}\)

Chọn B

B

cac ban giai giup minh voi

:(((

\(\dfrac{x-1}{2x^2-4x}-\dfrac{7}{8x}=\dfrac{5-x}{4x^2-8x}-\dfrac{1}{8x-16}\) ( ĐKXĐ: \(x\ne0;x\ne2\) )

\(\Leftrightarrow\dfrac{x-1}{2x\left(x-2\right)}-\dfrac{7}{8x}=\dfrac{5-x}{4x\left(x-2\right)}-\dfrac{1}{8\left(x-2\right)}\)

\(\Leftrightarrow\dfrac{\left(x-1\right)4}{8x\left(x-2\right)}-\dfrac{7\left(x-2\right)}{8x\left(x-2\right)}=\dfrac{2\left(5-x\right)}{8x\left(x-2\right)}-\dfrac{1x}{8x\left(x-2\right)}\)

\(\Rightarrow4x-4-7x+14=10-2x-x\)

\(\Leftrightarrow-3x+2x+x=10+4-14\)

\(\Leftrightarrow0=0\)

          Vậy pt đã cho có nghiệm đúng với mọi x

a) <=> 4x^3 - 12x^2 - x^2 + 3x + 6x - 18 = 0

<=> 4x^2 (x - 3) - x(x - 3) + 6(x - 3) = 0

<=> (x - 3)(4x^2 - x + 6) = 0

xét 2 th

. x - 3 = 0 <=> x = 3

. 4x^2 - x + 6 = 0

<=> 4x^2 + 2.(1/2)x + 1/4 + 23/4 = 0

<=> (4x + 1/2)^2 = -23/4

.... phần sau bạn tự làm nhé 

vậy pt trên có nghiệm là ...

. mik bận nên chỉ làm như vậy thôi.. những ý sau thì tách tương tự

c) => x³ + 2x² - 6x²  - 12x + 4x + 8 = 0

=> (x³ + 2x²)  -  (6x²  + 12x)  + (4x + 8) = 0

=> x². (x +2) - 6x. (x + 2) + 4.(x + 2) =0

=> (x +2).(x²  - 6x + 4) = 0

=> x+ 2 = 0 hoặc x²  - 6x + 4 = 0

+) x+ 2 =0 => x = -2

+) x²  - 6x + 4 = 0 => x²  - 2.x.3  + 9  - 5 = 0 => (x -3)²  = 5

=> x - 3 = \(\sqrt{5}\) hoặc x - 3 = - \(\sqrt{5}\)

=> x = 3 + \(\sqrt{5}\) hoặc x = 3 - \(\sqrt{5}\)

vậy...