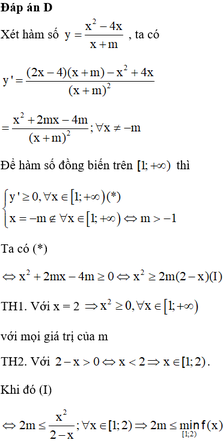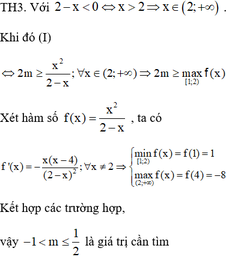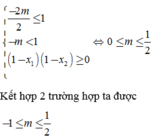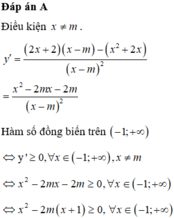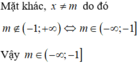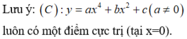Hàm số yx2−4xx+myx2-4xx+m đồng biến trên [1; +∞)[1; +∞) thì giá trị của m là:
Đọc tiếp
Hàm số đồng biến trên thì giá trị của m là:
Những câu hỏi liên quan
Hàm số
y
x
2
-
4
x
x
+
m
đồng biến trên
[
1
;
+
∞
)
thì giá trị của m là: A. m
∈
(
-
1
2
;
2
]
...
Đọc tiếp
Hàm số y = x 2 - 4 x x + m đồng biến trên [ 1 ; + ∞ ) thì giá trị của m là:
A. m ∈ ( - 1 2 ; 2 ] \ - 1
B. m ∈ ( - 1 ; 2 ] \ - 1
C. m ∈ ( - 1 ; 1 2 )
D. m ∈ ( - 1 ; 1 2 ]
Gọi x1, x2 là hai điểm cực trị của hàm số
y
x
2
-
4
x
x
+
1
Tính giá trị của biểu thức P x1.x2 A. P -5 B. P -2 C. P -1 D. P -4
Đọc tiếp
Gọi x1, x2 là hai điểm cực trị của hàm số y = x 2 - 4 x x + 1 Tính giá trị của biểu thức P = x1.x2
A. P = -5
B. P = -2
C. P = -1
D. P = -4
Đáp án D
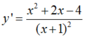
Gọi x1, x2 là hoành độ hai điểm cực trị.
Khi đó x1, x2 là hai nghiệm của phương trình y’ = 0
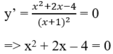
Theo định lý Vi-et, ta có x1.x2 = -4
Đúng 0
Bình luận (0)
Tìm m để hàm số
y
x
2
−
4
2
x
+
m
đồng biến trên đồng biến trên
1
;
+
∞
. A.
m
∈
−
4...
Đọc tiếp
Tìm m để hàm số y = x 2 − 4 2 x + m đồng biến trên đồng biến trên 1 ; + ∞ .
A. m ∈ − 4 ; 1 2 \ 0
B. m ∈ − 4 ; 1 2
C. m ∈ 0 ; 1 2
D. m ∈ − 1 2 ; 1 2
Cho hàm số
y
x
2
+
2
x
x
−
m
. Tìm m để hàm số đồng biến trên
−
1
;
+
∞
A.
m
∈
−
∞...
Đọc tiếp
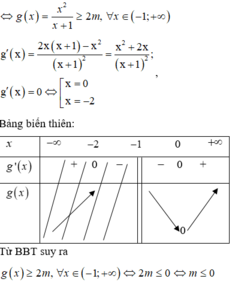
Cho hàm số y = x 2 + 2 x x − m . Tìm m để hàm số đồng biến trên − 1 ; + ∞
A. m ∈ − ∞ ; − 1
B. m ≤ 0
C. m ≥ − 1
D. m > − 1
Cho hàm số
y
x
2
+
2
x
x
-
m
. Tìm mđể hàm số đồng biến trên (-1;+∞) A. m∈├ -∞;-1┤ B. m≤0 C. m≥-1 D. m-1
Đọc tiếp
Cho hàm số y = x 2 + 2 x x - m . Tìm mđể hàm số đồng biến trên (-1;+∞)
A. m∈├ -∞;-1┤
B. m≤0
C. m≥-1
D. m>-1
Trong các hàm số
y
x
2
-
2
x
+
1
,
y
-
x
2
-
2
x
+
1
,
y
x
2
-
3
x
+
1
và
y
-...
Đọc tiếp
Trong các hàm số y = x 2 - 2 x + 1 , y = - x 2 - 2 x + 1 , y = x 2 - 3 x + 1 và y = - x 2 + 4 x + 1 , có bao nhiêu hàm số đồng biến trên khoảng 3 2 ; 2
A. 1
B. 2
C. 3
D. 4
Tìm m để hàm số
y
x
2
−
4
2
x
+
m
đồng biến trên
1
;
+
∞
. A.
m
∈
−
4...
Đọc tiếp
Tìm m để hàm số y = x 2 − 4 2 x + m đồng biến trên 1 ; + ∞ .
A. m ∈ − 4 ; 1 2 \ 0
B. m ∈ − 4 ; 1 2
C. m ∈ 0 ; 1 2
D. m ∈ − 1 2 ; 1 2
Đáp án D
Tập xác định
D = − ∞ ; − m ∪ − m ; + ∞ , y ' = x 2 + 2 m x − 4 m 2 x + m 2
TH1:
1 ; + ∞ ⊂ − m ; + ∞ ⇔ Δ ' = m 2 + 4 m < 0 − m < 1 ⇔ − 1 < m < 0
TH2: y'=0 có 2 nghiệm x 1 , x 2 thỏa mãn x 1 ≤ x 2 ≤ 1 và 1 ; + ∞ ⊂ − m ; + ∞
− 2 m 2 ≤ 1 − m < 1 1 − x 1 1 − x 2 ≥ 0 ⇔ 0 ≤ m ≤ 1 2
Kết hợp 2 trường hợp ta được − 1 ≤ m ≤ 1 2
Đúng 0
Bình luận (0)
Tìm m để hàm số y đồng biến trên R
a, y = mx - x2 - 2x + mx2 + m
b, (m2 - 3m +2).x2 + (m - 1).x + \(\sqrt{3}\)
Lời giải:
a. $y=mx-x^2-2x+mx^2+m=x^2(m-1)+x(m-2)+m$
Lấy $x_1,x_2\in R$ sao cho $x_1\neq x_2$
$y(x_1)=x_1^2(m-1)+x_1(m-2)+m$
$y(x_2)=x_2^2(m-1)+x_2(m-2)+m$
Để hàm đồng biến thì:
$\frac{y(x_1)-y(x_2)}{x_1-x_2}>0$
$\Leftrightarrow \frac{x_1^2(m-1)+x_1(m-2)+m-[x_2^2(m-1)+x_2(m-2)+m]}{x_1-x_2}>0$
$\Leftrightarrow \frac{(m-1)(x_1^2-x_2^2)+(m-2)(x_1-x_2)}{x_1-x_2}>0$
$\Leftrightarrow (m-1)(x_1+x_2)+(m-2)>0$
Với mọi $x_1,x_2\in\mathbb{R}$ thì không có cơ sở để tìm $m$ sao cho hàm đồng biến.
b.
Xét tương tự câu 1, với $x_1\neq x_2\in \mathbb{R}$ thì hàm đồng biến khi:
$(m^2-3m+2)(x_1+x_2)+(m-1)>0$
Với mọi $x_1, x_2\in\mathbb{R}$ thì điều này xảy ra khi:
$m^2-3m+2=0$ và $m-1>0$
$\Leftrightarrow (m-1)(m-2)=0$ và $m-1>0$
$\Leftrightarrow m=2$
Đúng 2
Bình luận (0)
Tìm m để hàm số
y
2
x
4
-
(
3
-
m
)
x
2
+
1
đồng biến trên
-
∞
;
+
∞
Đọc tiếp
Tìm m để hàm số y = 2 x 4 - ( 3 - m ) x 2 + 1 đồng biến trên - ∞ ; + ∞
Câu 94. Cho hàm số y =x2 đồng biến trên khoảng
A.R B.(0,+∞) C.R\{0} D.(-∞,0)
Câu 95. Đỉnh của parabol y=-x2 +2x+3 có tọa độ là bao nhiêu.
Câu 96. Hàm số y=-x2 +2x+3 đồng biến trên khoảng:
A.(-1,+∞)
B.(-∞,-1)
C.(1,+∞)
D.(-∞,1)
Câu 94: B
Câu 95: \(A=\left(-\dfrac{b}{2a};-\dfrac{b^2-4ac}{4a}\right)\)
\(\Leftrightarrow A\left(\dfrac{-2}{2\cdot\left(-1\right)};\dfrac{-\left(2^2-4\cdot\left(-1\right)\cdot3\right)}{4\cdot\left(-1\right)}\right)\)
\(\Leftrightarrow A\left(1;4\right)\)
Đúng 1
Bình luận (1)