
Những câu hỏi liên quan
cho xOy và tia Oz nằm giữa hai tia Ox và Oy. Từ điểm A trên tia Oz vẽ AH vuông góc Ox, AK vuông góc Oy. Kẻ HE vuông góc Oz
a) tính độ dài các đoạn thẳng OA, OH, AH và HE biết OE = 16cm, AE = 9cm
b) Gọi F là hình chiếu của K trên Oz, I là giao điểm của EF và HK. Chứng minh IE . KF = IF. HE
cíu tui cíu tui
Cho góc xoy và tia oz nằm giứa hai tia ox và oy . từ diểm A trên tia oz . vẽ AH vuông góc vơi ox ,AK vuông góc với oy . gọi ÈF lần lượt là hình chiếu của H và K trên oz . gọi B là giao điểm của HK và oz cmr:frac{EA.EO}{FA.FO} frac{BH^2}{BK^2} Mọi người ơi giúp mình vơi mình cần gấp(ai mà trả lời thì cho mình cám ơn nha)
Đọc tiếp
Cho góc xoy và tia oz nằm giứa hai tia ox và oy . từ diểm A trên tia oz . vẽ AH vuông góc vơi ox ,AK vuông góc với oy . gọi ÈF lần lượt là hình chiếu của H và K trên oz . gọi B là giao điểm của HK và oz
cmr:
\(\frac{EA.EO}{FA.FO}\) =\(\frac{BH^2}{BK^2}\)
Mọi người ơi giúp mình vơi mình cần gấp(ai mà trả lời thì cho mình cám ơn nha)
Có \(\Delta HEB~\Delta KFB\left(g-g\right)\)=> \(\frac{HE}{KF}=\frac{BH}{BK}\)=> \(\frac{HE^2}{KF^2}=\frac{BH^2}{BK^2}\)(1)
Có \(HE^2=EA.EO\)(TỰ XÉT TAM GIÁC NHA) (2)
\(KF^2=FA.FO\)(3)
tỪ (1),(2),(3) => \(\frac{EA.EO}{FA.FO}=\frac{BH^2}{BK^2}\)(đpcm)
Đúng 0
Bình luận (0)
ko có j đâu bạn mk biết làm nên mk nhắc thôi ^^
Đúng 0
Bình luận (0)
Cho góc xOy và tia Oz nằm giữa hai tia Ox và Oy. Từ điểm A trên tia Oz vẽ AH\(⊥\)Ox, AK \(⊥\)Oy. Gọi E, F lần lượt là hình chiếu của H và K trên Oz, gọi B là giao điểm của HK và Oz. Chứng minh rằng: \(\frac{EA.EO}{FA.FO}\)= \(\frac{BH^2}{BK^2}\).MÌNH ĐANG CẦN GẤP, CẢM ƠN CÁC BẠN NHIỀU :P
Cho góc xOy = 60 độ. Vẽ tia pg Oz của góc xOy. Trên tia Õ kaays A, trên tia Oy lấy B: OA = OB. AB cắt Oz tại I
a/ CMR OI vuông với AB
b/ Trên tia Oz lấy M. CMR MA = MB
c/ Qua M vẽ đg thẳng song song với AB, cát Ox, Oy lần lượt tại C và D. CMR BD = AC
e/ Gọi H là giao điểm của AM và IC, K là giao điểm BM và ID. CMR Oz là trung trực HK
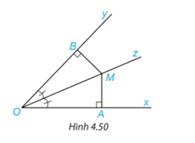
Cho Oz là tia phân giác của góc xOy. Lấy điểm M trên tia Oz và hai điểm A, B lần lượt trên các tia Ox, Oy sao cho MA vuông góc với Ox, MB vuông góc với Oy(H.4.50). Chứng minh rằng MA = MB.
Xét hai tam giác vuông OBM và OAM có:
OM chung
\(\widehat {BOM} = \widehat {AOM}\) (gt)
\( \Rightarrow \Delta OBM = \Delta OAM\)(cạnh huyền – góc nhọn)
Suy ra MB=MA ( 2 cạnh tương ứng)
Đúng 1
Bình luận (0)
Cho góc \(xOy\) khác góc bẹt, Oz là tia phân giác. Trên các tia Ox, Oy lần lượt lấy các điểm A, B sao cho OA = OB. C là điểm trên tia Oz. Gọi D là giao điểm của AC và Oy, E là giao điểm của BC và Ox. Chứng minh:
a) AC = BC
b) △BCD = △ACE
!!CÓ VẼ HÌNH!!
cho góc nhọn xOy có Oz là tia phân giác của góc này . trên tia Ox lấy điểm A trên tia Oy lấy điểm Bsao cho OA=OB ; M là một điểm ( khác O ) thuộc tia Oz .
a) chứng minh tam giác AOM =tam giác BOM
b) từ A dựng AH vuông góc với Oy , từ B dựng BK vuông góc Ox . chứng minh AH= BK
c) gọi giao điểm AH và BK là I . chứng tỏ rằng điểm I cũng thuộc tia phân giác Oz
Cho góc nhọn xOy, vẽ tia phân giác Oz của góc xOy, trên tia Oz lấy C. Từ C kẻ CA vuông góc với tia Ox (A thuộc Ox), kẻ CB vuông góc với tia Oy (B thuộc Oy). CMR:
a) CA = CB (Câu này mình làm được rồi)
b) Gọi E là giao điểm của AC và Oy, F là giao điểm của BC và Ox. CMR: Tam giác CEF cân
c) AC < CE
a/Xét tam giác OCA và tam giác OCB:
OC chung
OAC=OBC(90 độ)
Góc AOC=BOC(Phân giác Oz)
=> Tam giác OCA=OCB(ch-gn)
=> CA=CB(cạnh tương ứng)
b/ Xét tam giác CAF và tam giác CBE:
Góc ACF=BCE(đối đỉnh)
Góc CBE=CAF(90 độ)
AC=CB(câu a)
=> Tma giác CAF=tam giác CBE(ch-gn)
=> CF=CE(cạnh tương ứng)
=> Tam giác CEF cân tại C
c/Xét tam giác vuông CBE có:
CE là cạnh huyền.
=> CE>CB Mà CB=CA
=> CE>CA(đpcm)
Đúng 0
Bình luận (0)
Bạn tự vẽ hình nha![]()
b.
Xét tam giác AFC và tam giác BEC có:
FAC = EBC ( = 90 )
AC = BC (theo câu a)
ACF = BCE (2 góc đối đỉnh)
=> Tam giác AFC = Tam giác BEC (g.c.g)
=> CF = CE (2 cạnh tương ứng)
=> Tam giác CEF cân tại C
c.
Tam giác BCE vuông tại B có:
BC < CE (quan hệ giữa góc và cạnh đối diện trong tam giác vuông)
mà BC = AC (theo câu a)
=> AC < CE
Chúc bạn học tốt![]()
Đúng 0
Bình luận (0)
Cho góc xOy. Điểm H nằm trên Oz tia phân giác của góc xOy. Từ H dựng các đường vuông góc xuống hai cạnh Ox và Oy ( A thuộc Ox ; B thuộc Oy )
a) CM: tam giác HAB cân
b) Gọi H là hình chiếu của điểm A nên Oy ; C là giao điểm của AD với DH và CM ; BC vuông góc Ox
c) Khi góc zOy = 600 ; OH = 4cm.Tính độ dài OA
các bạn ơi giúp mình với
a.
Xét tam giác AHO vuông tại A và tam giác BHO vuông tại B có:
AOH = BOH (OH là tia phân giác của AOB)
OH là cạnh chung
=> Tam giác AHO = Tam giác BHO (cạnh huyền - góc nhọn)
=> AH = BH (2 cạnh tương ứng)
=> Tam giác HAB cân tại H
b.
OA = OB (tam giác AHO = tam giác BHO)
=> Tam giác OAB cân tại O
OH là tia phân giác của tam giác OBA cân tại O
=> OH là đường cao của tam giác OBA
mà AD là đường cao của tam giác OAB
=> C là trực tâm của tam giác OAB
=> BC là đường cao của tam giác OAB
=> BC _I_ Ox
Chúc bạn học tốt![]()
Đúng 0
Bình luận (1)
Phương An làm 2 câu a,b giờ tớ làm câu c luôn nhé ;)
Ta thấy tam giác HAO là tam giác có 1 góc là 30 độ nên HO=2OA = > OA =2 (cm)
Dựa vào tính chất trong 1 tam giác có 1 góc là 30 độ thì cạnh huyền gấp 2 lần cạnh đối diện với góc 30 độ
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho 150 .o xOy Vẽ các tia Oz và Ot nằm trong góc xOy sao cho Oz vuông góc với Ox và Ot vuông góc với Oy. a) Chứng minh xOt yOz . b) Gọi Om, On lần lượt là hai tia phân giác của hai góc xOt và yOz . Tính số đo mOn .



















