`@` `\text {Ans}`

`\downarrow`

`a)`

Thu gọn:

`P(x)=`\(5x^4 + 3x^2 - 3x^5 + 2x - x^2 - 4 +2x^5\)

`= (-3x^5 + 2x^5) + 5x^4 + (3x^2 - x^2) + 2x - 4`

`= -x^5 + 5x^4 + 2x^2 + 2x - 4`

`Q(x) =`\(x^5 - 4x^4 + 7x - 2 + x^2 - x^3 + 3x^4 - 2x^2\)

`= x^5 + (-4x^4 + 3x^4) - x^3 + (x^2 - 2x^2) + 7x - 2`

`= x^5 - x^4 - x^3 - x^2 + 7x - 2`

`@` Tổng:

`P(x)+Q(x)=`\((-x^5 + 5x^4 + 2x^2 + 2x - 4) + (x^5 - x^4 - x^3 - x^2 + 7x - 2)\)

`= -x^5 + 5x^4 + 2x^2 + 2x - 4 + x^5 - x^4 - x^3 - x^2 + 7x - 2`

`= (-x^5 + x^5) - x^3 + (5x^4 - x^4) + (2x^2 - x^2) + (2x + 7x) + (-4-2)`

`= 4x^4 - x^3 + x^2 + 9x - 6`

`@` Hiệu:

`P(x) - Q(x) =`\((-x^5 + 5x^4 + 2x^2 + 2x - 4) - (x^5 - x^4 - x^3 - x^2 + 7x - 2)\)

`= -x^5 + 5x^4 + 2x^2 + 2x - 4 - x^5 + x^4 + x^3 + x^2 - 7x + 2`

`= (-x^5 - x^5) + (5x^4 + x^4) + x^3 + (2x^2 + x^2) + (2x - 7x) + (-4+2)`

`= -2x^5 + 6x^4 + x^3 + 3x^2 - 5x - 2`

`b)`

`@` Thu gọn:

\(H (x) = ( 3x^5 - 2x^3 + 8x + 9) - ( 3x^5 - x^4 + 1 - x^2 + 7x)\)

`= 3x^5 - 2x^3 + 8x + 9 - 3x^5 + x^4 - 1 + x^2 - 7x`

`= (3x^5 - 3x^5) + x^4 - 2x^3 - x^2 + (8x + 7x) + (9+1)`

`= x^4 - 2x^3 - x^2 + 15x + 10`

\(R( x) = x^4 + 7x^3 - 4 - 4x ( x^2 + 1) + 6x\)

`= x^4 + 7x^3 - 4 - 4x^3 - 4x + 6x`

`= x^4 + (7x^3 - 4x^3) + (-4x + 6x) - 4`

`= x^4 + 3x^3 + 2x - 4`

`@` Tổng:

`H(x)+R(x)=` \((x^4 - 2x^3 - x^2 + 15x + 10)+(x^4 + 3x^3 + 2x - 4)\)

`= x^4 - 2x^3 - x^2 + 15x + 10+x^4 + 3x^3 + 2x - 4`

`= (x^4 + x^4) + (-2x^3 + 3x^3) - x^2 + (15x + 2x) + (10-4)`

`= 2x^4 + x^3 - x^2 + 17x + 6`

`@` Hiệu: 

`H(x) - R(x) =`\((x^4 - 2x^3 - x^2 + 15x + 10)-(x^4 + 3x^3 + 2x - 4)\)

`=x^4 - 2x^3 - x^2 + 15x + 10-x^4 - 3x^3 - 2x + 4`

`= (x^4 - x^4) + (-2x^3 - 3x^3) - x^2 + (15x - 2x) + (10+4)`

`= -5x^3 - x^2 + 13x + 14`

`@` `\text {# Kaizuu lv u.}`

\(a,\Leftrightarrow\left(4x-8\right)\left(x+1\right)=0\\ \Leftrightarrow4\left(x-2\right)\left(x+1\right)=0\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-1\end{matrix}\right.\\ b,\Leftrightarrow\left(x+1\right)\left(x^2+1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=-1\\x^2=-1\left(vô.lí\right)\end{matrix}\right.\Leftrightarrow x=-1\\ c,\Leftrightarrow x^2-2x-4x+8=0\\ \Leftrightarrow\left(x-2\right)\left(x-4\right)=0\Leftrightarrow\left[{}\begin{matrix}x=2\\x=4\end{matrix}\right.\\ d,\Leftrightarrow x^3-3x^2+3x-9x+2x-6=0\\ \Leftrightarrow\left(x-3\right)\left(x^2+3x+2\right)=0\\ \Leftrightarrow\left(x-3\right)\left(x^2+x+2x+2\right)=0\\ \Leftrightarrow\left(x-3\right)\left(x+1\right)\left(x+2\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=3\\x=-1\\x=-2\end{matrix}\right.\)

a) \(\Rightarrow4\left(x+1\right)\left(x-2\right)=0\)

\(\Rightarrow\left[{}\begin{matrix}x=-1\\x=2\end{matrix}\right.\)

b) \(\Rightarrow x^2\left(x+1\right)+\left(x+1\right)=0\)

\(\Rightarrow\left(x+1\right)\left(x^2+1\right)=0\)

\(\Rightarrow x=-1\left(do.x^2+1\ge1>0\right)\)

c) \(\Rightarrow x\left(x-4\right)-2\left(x-4\right)=0\)

\(\Rightarrow\left(x-4\right)\left(x-2\right)=0\)

\(\Rightarrow\left[{}\begin{matrix}x=4\\x=2\end{matrix}\right.\)

d) \(\Rightarrow x^2\left(x-3\right)+3x\left(x-3\right)+2\left(x-3\right)\)

\(\Rightarrow\left(x-3\right)\left(x^2+3x+2\right)=0\)

\(\Rightarrow\left(x-3\right)\left(x+1\right)\left(x+2\right)=0\)

\(\Rightarrow\left[{}\begin{matrix}x=3\\x=-2\\x=-1\end{matrix}\right.\)

\(\left(x+3\right)\left(x^2-3x+9\right)=7x^3+21x\\ \Leftrightarrow x^3+27=7x^3+21x\\ \Leftrightarrow6x^3+21x-27=0\\ \Leftrightarrow\left(6x^3-6x^2\right)+\left(6x^2-6x\right)+\left(27x-27\right)=0\\ \Leftrightarrow\left(x-1\right)\left(6x^2+6x+27\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x-1=0\\6x^2+6x+27=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=1\\6\left(x^2+x+\dfrac{1}{4}\right)+\dfrac{51}{2}=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=1\\6\left(x+\dfrac{1}{2}\right)^2+\dfrac{51}{2}=0\left(vô.lí\right)\end{matrix}\right.\)

Vậy \(x=1\)

\(\Leftrightarrow x^3+27-7x^3-21x=0\)

\(\Leftrightarrow-6x^3-21x+27=0\)

\(\Leftrightarrow-6x^3+6x-27x+27=0\)

\(\Leftrightarrow-6x\left(x-1\right)\left(x+1\right)-27\left(x-1\right)=0\)

\(\Leftrightarrow\left(x-1\right)\left(6x^2+6x+27\right)=0\)

hay x=1

`A(x)=7x^3-5x^2-7x+3-7x^3+5x^2+17x+27`

`A(x)=(7x^3-7x^3)-(5x^2-5x^2)+(-7x+17x)+(3+27)`

`A(x)=10x+30`

Cho `A(x)=0`

`=>10x+30=0`

`=>10x=-30`

`=>x=-3`

Vậy nghiệm của đa thức `A(x)` là `x=-3`

Đặt \(A\left(x\right)=0\)

\(\rightarrow7x^3-5x^2-7x+3-7x^3+5x^2+17x+27=0\)

\(\Leftrightarrow10x+30=0\)

\(\Leftrightarrow10x=-30\)

\(\Leftrightarrow x=-3\)

Vậy \(x=-3\) là nghiệm của đa thức \(A\left(x\right)\)

A(x) = 7x³ - 5x² - 7x + 3 - 7x³ + 5x² +17x +27

= 10x + 30

đặt A(x) = 0

<=> 10x + 30 = 0

<=> 10x = -30

<=> x = -3

vậy x = -3 là nghiệm của A(x)

a) \(7x\left(2x-3\right)-\left(4x^2-9\right)=0\Rightarrow7x\left(2x-3\right)-\left(2x-3\right)\left(2x+3\right)=0\Rightarrow\left(2x-3\right)\left(7x-2x+3\right)=0\Rightarrow\left[{}\begin{matrix}2x-3=0\\5x+3=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=\dfrac{3}{2}\\x=-\dfrac{3}{5}\end{matrix}\right.\)

b) \(\left(2x-7\right).\left(x-2\right)\left(x^2-4\right)=0\Rightarrow\left(2x-7\right)\left(x-2\right)^2\left(x+2\right)=0\Rightarrow\left[{}\begin{matrix}2x-7=0\\\left(x-2\right)^2=0\\x+2=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=\dfrac{7}{2}\\x=2\\x=-2\end{matrix}\right.\)

c)\(\left(9x^2-25\right)-\left(6x-10\right)=0\Rightarrow\left(3x-5\right)\left(3x+5\right)-2\left(3x-5\right)=0\Rightarrow\left(3x-5\right)\left(3x+5-2\right)=0\Rightarrow\left[{}\begin{matrix}3x-5=0\\3x+3=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=\dfrac{5}{3}\\x=1\end{matrix}\right.\)

a: Ta có: \(7x\left(2x-3\right)-\left(4x^2-9\right)=0\)

\(\Leftrightarrow7x\left(2x-3\right)-\left(2x-3\right)\left(2x+3\right)=0\)

\(\Leftrightarrow\left(2x-3\right)\left(5x-3\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{3}{2}\\x=\dfrac{3}{5}\end{matrix}\right.\)

b: Ta có: \(\left(2x-7\right)\left(x-2\right)\left(x^2-4\right)=0\)

\(\Leftrightarrow\left(2x-7\right)\left(x-2\right)^2\cdot\left(x+2\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{7}{2}\\x=2\\x=-2\end{matrix}\right.\)

c: Ta có: \(\left(9x^2-25\right)-\left(6x-10\right)=0\)

\(\Leftrightarrow\left(3x-5\right)\left(3x+5-2\right)=0\)

\(\Leftrightarrow\left(3x-5\right)\left(3x+3\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5}{3}\\x=-1\end{matrix}\right.\)

 Ta thấy \(B=\left(x-1\right)\left(x-5\right)\) nên để đa thức A chia hết cho đa thức B thì \(A=\left(x-1\right)\left(x-5\right).C\) với \(C\) là một đa thức bậc 2 hệ số nguyên theo \(x\).

 Điều này tương đương với việc \(A\) có 2 nghiệm là \(x=1,x=5\). Do đó \(A\left(1\right)=0\) \(\Leftrightarrow1^4-7.1^3+10.1^2+\left(a-1\right)+b-a=0\) \(\Leftrightarrow b=-3\)

 Ta viết lại \(A=x^4-7x^3+10x^2+\left(a-1\right)x-3-a\). Ta có \(A\left(5\right)=0\) \(\Leftrightarrow5^4-7.5^3+10.5^2+\left(a-1\right).5-3-a=0\) \(\Leftrightarrow4a-8=0\) \(\Leftrightarrow a=2\).

 Vậy để đa thức A chia hết cho đa thức B thì \(a=2,b=-3\).

A:B=x2-x+11 dư (a+70)x+b-a-55

Để A chia hết cho B thì

(a+70)x+b-a-55=0

b-a-55=0 (a khác -70) tại x=0

Vậy b-a=55 thỏa đề bài

a: P(x)=6x^3-4x^2+4x-2

Q(x)=-5x^3-10x^2+6x+11

M(x)=x^3-14x^2+10x+9

b: \(C\left(x\right)=7x^4-4x^3-6x+9+3x^4-7x^3-5x^2-9x+12\)

=10x^4-11x^3-5x^2-15x+21

Ta có

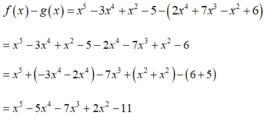
Sắp xếp theo lũy thừa tăng dần của biến ta được

- 11   +   2 x 2   -   7 x 3   -   5 x 4   +   x 5

Chọn đáp án B