1+36

Những câu hỏi liên quan
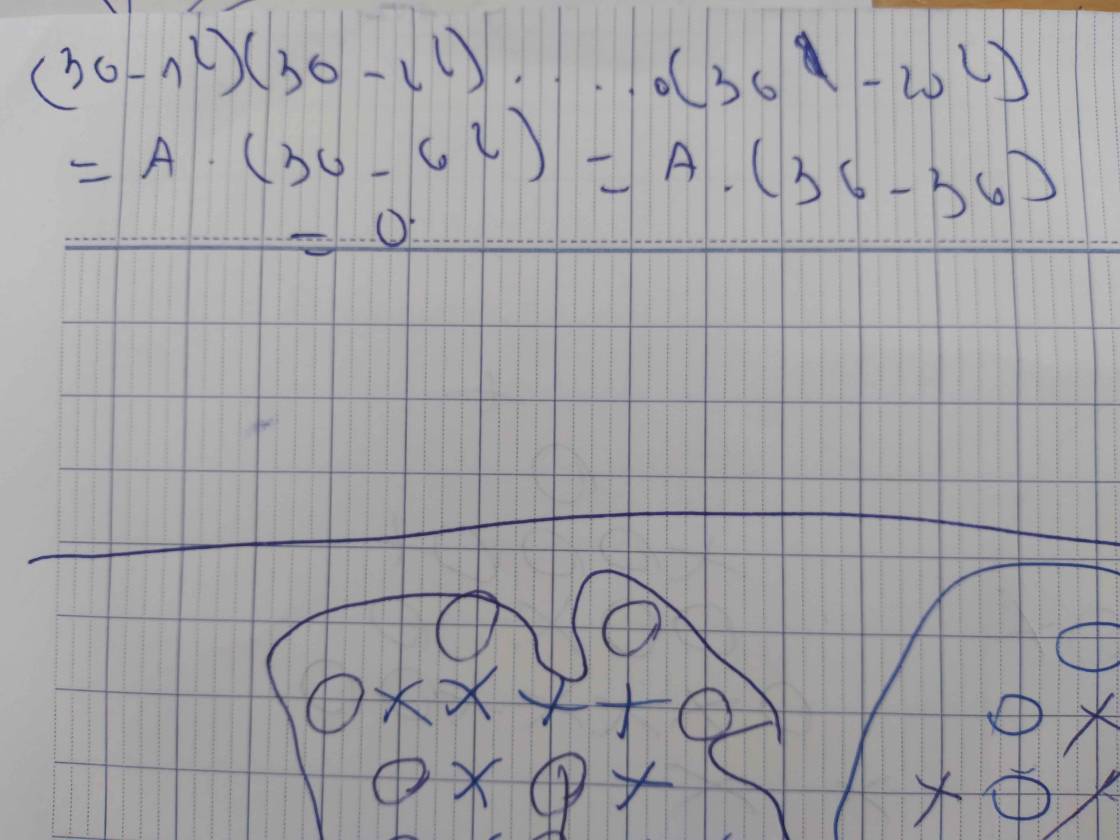
tính nhanh (36 - 1^2).(36 - 2^2).(36 - 3^2)....(36 - 20 ^2 )
(36 - 1²).(36 - 2²).(36 - 3²)...(36 - 20²)
= (36 - 1²).(36 - 2²)...(36 - 6²)...(36 - 20²)
= (36 - 1²).(36 - 2²)...(36 - 36)...(36 - 20²)
= (36 - 1²)(36 - 2²)...0...(36 - 20²)
= 0
Đúng 1
Bình luận (0)
E = 36 / 1.7 + 36 / 7.13 + 36 / 13.19 + .... + 36 / 94.100
F = 1 / 10 + 1 / 40 + 1 / 88 + .... + 1 / ( 3a+z) ( 3a+ 5)
G = 1 / 2.3 + 2 / 3.5 + 3 / 5.8 + 4 / 8.12 + 5 / 12.17
E = \(\frac{36}{1\cdot7}+\frac{36}{7\cdot13}+...+\frac{36}{94\cdot100}=\frac{36}{6}\left[\frac{1}{1\cdot7}+\frac{1}{7\cdot13}+...+\frac{1}{94\cdot100}\right]\)
\(=6\left[1-\frac{1}{7}+\frac{1}{7}-\frac{1}{13}+...+\frac{1}{94}-\frac{1}{100}\right]=6\left[1-\frac{1}{100}\right]\)
\(=6\cdot\frac{99}{100}=\frac{297}{50}\)
F = \(\frac{1}{10}+\frac{1}{40}+\frac{1}{88}+...+\frac{1}{\left[3a+2\right]\left[3a+5\right]}\)
\(=\frac{1}{2\cdot5}+\frac{1}{5\cdot8}+\frac{1}{8\cdot11}+...+\frac{1}{\left[3a+2\right]\left[3a+5\right]}\)
\(=\frac{1}{3}\left[\frac{1}{2}-\frac{1}{5}+\frac{1}{5}-\frac{1}{8}+\frac{1}{8}-\frac{1}{11}+...+\frac{1}{3a+2}-\frac{1}{3a+5}\right]\)
\(=\frac{1}{3}\left[\frac{1}{2}-\frac{1}{3a+5}\right]=\frac{1}{6}-\frac{1}{9a+15}\)
G = \(\frac{1}{2\cdot3}+\frac{2}{3\cdot5}+\frac{3}{5\cdot8}+\frac{4}{8\cdot12}+\frac{5}{12\cdot17}=\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{5}+...+\frac{1}{12}-\frac{1}{17}\)
\(=\frac{1}{2}-\frac{1}{17}=\frac{15}{34}\)
Đúng 0
Bình luận (0)
E=36/1-36/7+36/7-36/13+...+36/94-36/100
=36-36/100=891/25
Đúng 0
Bình luận (0)
36/(1*3*5) + 36/(3*5*7) + 36/(5*7*9) + ... + 36/(25*27*29)
1, Chứng minh
a) A=\(\dfrac{1}{1.2.3}+\dfrac{1}{2.3.4}+\dfrac{1}{3.4.5}+....+\dfrac{1}{18.19.20}< \dfrac{1}{4}\)
b) B=\(\dfrac{36}{1.3.5}+\dfrac{36}{3.5.7}+\dfrac{36}{5.7.9}+....+\dfrac{36}{25.26.27}< 3\)
a, A= 1/2. (2/1.2.3+2/2.3.4+2/3.4.5+...+2/18.19.20) A=1/2. (1/1.2-1/2.3+1/2.3-1/3.4+1/3.4-1/4.5+...+1/18.19-1/19.20) A=1/2. (1/1.2-1/19.20) A=1/2. 189/380 A= 189/760
Đúng 0
Bình luận (0)
A = 1/1x2x3 + 1/2x3x4 + 1/3x4x5 +...+ 1/18x19x20 < 1/4B = 36/1x3x5 + 36/3x5x7 + 36/5x7x9 +...+ 36/25x27x29 < 3C = 1/2^2 + 1/3^2 + 1/4^2 +...+ 1/100^2 < 1D = 1/101 + 1/102 + 1/103 +...+ 1/999 + 1/200 > 7/12
Xem chi tiết
2A=\(\frac{2}{1.2.3}\)+\(\frac{2}{2.3.4}\)+...+\(\frac{2}{18.19.20}\)
=1/1.2-1/2.3+1/2.3-1/3.4+...+1/18.19-1/19.20
=1/2-1/19.20
A=1/4-1/19.20.2
vậy A<1/4
Đúng 0
Bình luận (0)
Áp dụng tính chất của một số với một tổng để tính (theo mẫu):
Mẫu: 36 x 11 = 36 x (10 +1)
= 36 x 10 + 36 x 1
= 360 + 36 = 396
a) 26 x 11
35 x 101
b) 213 x 11
123 x 101
a) 26 x 11 = 26 x (10 + 1)
= 26 x 10 + 26 x 1 = 260 + 26 = 286
35 x 101 = 35 x (100 + 1)
= 35 x 100 + 35 x 1 = 3500 + 35 = 3535
b) 213 x 11 = 213 x (10 +1)
= 213 x 100 + 213 x 1 = 2130 + 213 = 2343
123 x 101 = 123 x (100 + 1)
= 123 x 100 + 123 x 1
= 12300 + 123 = 12423
Nói thêm: Muốn nhân một số với 11 (hoặc 101) ta nhân số đó với 10 (hoặc 100) rồi cộng thêm chính số đó.
Đúng 1
Bình luận (0)
CTR:36/1*3*5+36/3*5*7+36/5*7*9+...+36/25*27*29<3
Tính tổng: A=36/(1*3*5)+36/(3*5*7)+36/(5*7*9)+...+36/(45*47*49)
Chứng minh rằng :
a) A=\(\frac{1}{1.2.3}+\frac{1}{2.3.4}+\frac{1}{3.4.5}+...+\frac{1}{18.19.20}<\frac{1}{4}\)
b) B=\(\frac{36}{1.3.5}+\frac{36}{3.5.7}+\frac{36}{5.7.9}+...+\frac{36}{25.27.29}<3\)
$\frac{4}{n\left(n+2\right)\left(n+4\right)}=\frac{n+4-n}{n\left(n+2\right)\left(n+4\right)}=\frac{1}{n\left(n+2\right)}-\frac{1}{\left(n+2\right)\left(n+4\right)}$4n(n+2)(n+4) =n+4−nn(n+2)(n+4) =1n(n+2) −1(n+2)(n+4) $\frac{B}{9}=\frac{1}{1.3}-\frac{1}{3.5}+\frac{1}{3.5}-\frac{1}{5.7}+...+\frac{1}{25.27}-\frac{1}{27.29}=\frac{1}{3}-\frac{1}{27.29}<\frac{1}{3}$B9 =11.3 −13.5 +13.5 −15.7 +...+125.27 −127.29 =13 −127.29 <13 $\Rightarrow B<3$
Đúng 1
Bình luận (0)
Câu 1. Một số tự nhiên a khác 0 nhỏ nhất thỏa mãn a⋮12 và a⋮36. Khi đó a là *
A. ƯC(12, 36).
B. BC(12, 36).
C. ƯCLN(12, 36).
D. BCNN(12, 36).
Xem thêm câu trả lời