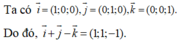ox là j v

Những câu hỏi liên quan
Trong mặt phẳng với hệ tọa độ Oxy, cho parabol
(
P
)
:
y
x
2
−
4
và parabol (P) là ảnh của (P) qua phép tịnh tiến theo
v
→
0
;
b
, với 0b4. Gọi A,B là giao điểm của (P) với Ox, M,N là giao điểm của (P) với Ox , I, J lần lượt là đỉnh của (P) và (P). Tìm tọa độ điểm J để...
Đọc tiếp
Trong mặt phẳng với hệ tọa độ Oxy, cho parabol ( P ) : y = x 2 − 4 và parabol (P') là ảnh của (P) qua phép tịnh tiến theo v → = 0 ; b , với 0<b<4. Gọi A,B là giao điểm của (P) với Ox, M,N là giao điểm của (P') với Ox , I, J lần lượt là đỉnh của (P) và (P'). Tìm tọa độ điểm J để diện tích tam giác IAB bằng 8 lần diện tích tam giác JMN.
A. J 0 ; − 1 5 .
B. J 0 ; 1 .
C. J 0 ; − 4 5 .
D. J 0 ; − 1 .
Đáp án D
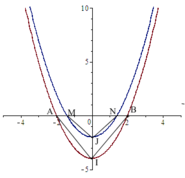
Phép tịnh tiến theo v → 0 ; b biến parabol P : y = x 2 − 4 thành parabol P ' : y = x 2 − 4 + b
Giao điểm của A,B với Ox của (P) có tọa độ lần lượt là: − 2 ; 0 , 2 ; 0
Giao điểm M,N với Ox của (P) có toạn độ lần lượt là: − 4 − b ; 0 , 4 − b ; 0
Đỉnh I,J của parabon (P), (P') có tọa độ lần lượt: 0 ; − 4 , 0 ; − 4 + b
Diện tích tam giác IAB bằng 8 lần diện tích tam giác JMN nên ta có:
I O . A B = 8 J O . M N ⇔ 4.4 = 8. 4 − b .2 4 − b ⇔ 4 − b 3 = 1 ⇔ b = 3 ⇒ J 0 ; − 1
Đúng 0
Bình luận (0)
Cho góc nhon xOy. Trên Ox lấy điểm A và trên Oy lấy điểm B sao cho OA=OB. Đường vuông góc với Ox kẻ qua A cắt Oy tại C. Đường vuông góc với Oy kẻ qua B cắt Ox tại D và cắt AC tại I. Đường vuông góc với Ox kẻ qua D cắt Oy tại E. Đường vuông góc với Oy kẻ qua C cắt Ox tại F và cắt DE tại J. Chứng minh 3 điểm O, I, J thẳng hàng
Cho một góc nhọn xOy và một đường thẳng d cắt Ox tại I, cắt Oy tại J, A và B là hai điểm thuộc đoạn thẳng IJ. Tìm một điểm M trên Ox và một điểm N trên Oy sao cho tổng MA + MN + NB nhỏ nhất
Trong không gian Oxyz với
i
→
,
j
→
,
k
→
lần lượt là các vecto đơn vị trên các trục Ox, Oy, Oz Tính tọa độ của vecto
i
→
+
j
→
-
k
→
Đọc tiếp
Trong không gian Oxyz với i → , j → , k → lần lượt là các vecto đơn vị trên các trục Ox, Oy, Oz Tính tọa độ của vecto i → + j → - k →
![]()
![]()
![]()
![]()
Trong mặt phẳng toạ độ Oxy, cho \(\overrightarrow i \)và \(\overrightarrow j \) là vectơ đơn vị trên trục hoành Ox và ở trên trục tung Oy
a) Tính \({\overrightarrow i ^2};{\overrightarrow j ^2};\overrightarrow i .\overrightarrow j .\)
b) Cho \(\overrightarrow u = \left( {{x_1},{y_1}} \right)\), \(\overrightarrow v = \left( {{x_2},{y_2}} \right)\). Tính tích vô hướng \(\overrightarrow u .\overrightarrow v \).
a) Ta có: \({\overrightarrow i ^2} = {\left| {\overrightarrow i } \right|^2} = 1;{\overrightarrow j ^2} = {\left| {\overrightarrow j } \right|^2};\overrightarrow i .\overrightarrow j = 0\)(vì \(\overrightarrow i \bot \overrightarrow j \) )
b) Ta có: \(\overrightarrow u .\overrightarrow v = \left( {{x_1}\overrightarrow i + {y_1}\overrightarrow j } \right).\left( {{x_2}\overrightarrow i + {y_2}\overrightarrow j } \right) = {x_1}{x_2}.{\overrightarrow i ^2} + {x_1}{y_2}.\left( {\overrightarrow i .\overrightarrow j } \right) + {y_1}{x_2}.\left( {\overrightarrow j .\overrightarrow i } \right) + {y_1}{y_2}.{\overrightarrow j ^2} = {x_1}{x_2} + {y_1}{y_2}\)
Đúng 0
Bình luận (0)
cho góc xoy nhọn.lấy a thuộc ox ,b thuộc oy sao cho OAOBđường vuông góc với ox kẻ từ A cắt Oy tại C.đường vuông góc với oy kẻ từ B cắt ox tại D và cắt AC tại Iđường vuông góc với ox kẻ từ D cắt oy tại Eđường vuông góc với oy kẻ từ C cắt ox tại F và cắt OE tại Jc/m:a, OI là tia phân giác của góc xoyb,OCOBOJ là tia phân giác của góc xoy c, O;I;J thẳng hàng
Đọc tiếp
cho góc xoy nhọn.lấy a thuộc ox ,b thuộc oy sao cho OA=OB
đường vuông góc với ox kẻ từ A cắt Oy tại C.đường vuông góc với oy kẻ từ B cắt ox tại D và cắt AC tại I
đường vuông góc với ox kẻ từ D cắt oy tại E
đường vuông góc với oy kẻ từ C cắt ox tại F và cắt OE tại J
c/m:
a, OI là tia phân giác của góc xoy
b,OC=OB
OJ là tia phân giác của góc xoy
c, O;I;J thẳng hàng
mấy bn giúp mk với bn nào nhanh nhất mk tặng 3
Đúng 0
Bình luận (0)
Cho đường thẳng xy lấy điểm O. Trên tia Ox lấy đoạn thẳng OA=5cm, trên tia Oy lấy điểm B sao cho OB=7cm. Gọi I là trung diem của AB, J là trung điểm của AI. Chứng tỏ: I và J khác phía
Cho đường thẳng xy lấy điểm O. Trên tia Ox lấy đoạn thẳng OA=5cm, trên tia Oy lấy điểm B sao cho OB=7cm. Gọi I là trung diem của AB, J là trung điểm của AI. Chứng tỏ: I và J khác phía
Trên đường thẳng xy cho điểm O. Trên tia Ox lấy đoạn thẳng OA = 5cm, trên tia Oy lấy đoạn thẳng OB = 7cm. Gọi I là trung điểm của AB, J là trung điểm của AI. Chứng tỏ I và J khác phía với O.
x.6=15.10
x.6=150
x=150:6
x=25
nóng quá đổi màu xanh cho mát
Đúng 0
Bình luận (0)
Songoku Sky Fc11 viết cái gì không đọc được
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho đường thẳng xy lấy điểm O. Trên tia Ox lấy đoạn thẳng OA=5cm, trên tia Oy lấy điểm B sao cho OB=7cm. Gọi I là trung diem của AB, J là trung điểm của AI. Chứng tỏ: I và J khác phía