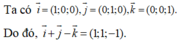Các câu hỏi tương tự
Trong không gian với hệ trục tọa độ Oxyz, các véctơ đơn vị trên các trục Ox, Oy, Oz lần lượt là
i
→
,
j
→
,
k
→
, cho điểm M(2;-1;1). Khẳng định nào sau đây là đúng?
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, các véctơ đơn vị trên các trục Ox, Oy, Oz lần lượt là i → , j → , k → , cho điểm M(2;-1;1). Khẳng định nào sau đây là đúng?
![]()
![]()
![]()
![]()
Trong không gian Oxyz cho một vecto
a
→
tùy ý khác vecto
0
→
. Gọi
α
,
β
,
γ
là ba góc tạo bởi ba vecto đơn vị
i
→
,
j
→
,
k
→
trên ba trục Ox, Oy, Oz v...
Đọc tiếp
Trong không gian Oxyz cho một vecto a → tùy ý khác vecto 0 → . Gọi α , β , γ là ba góc tạo bởi ba vecto đơn vị i → , j → , k → trên ba trục Ox, Oy, Oz và vecto a → . Chứng minh rằng: cos 2 α + cos 2 β + cos 2 γ = 1
Trong không gian Oxyz, cho một điểm M. Hãy phân tích vecto O M → theo ba vecto không đồng phẳng i → , j → , k → đã cho trên các trục Ox, Oy, Oz.
Trong không gian với hệ trục tọa độ Oxyz, cho điểm M(1;2;3). Gọi A, B, C lần lượt là hình chiếu của M trên các trục Ox, Oy, Oz. Viết phương trình mặt phẳng (ABC).
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho điểm M(1;2;3). Gọi A, B, C lần lượt là hình chiếu của M trên các trục Ox, Oy, Oz. Viết phương trình mặt phẳng (ABC).
![]()
![]()
![]()
![]()
Trong không gian với hệ trục tọa độ Oxyz, cho điểm M (-2;-1;3). Phương trình mặt phẳng đi qua các điểm lần lượt là hình chiếu của điểm M lên các trục tọa độ Ox, Oy, Oz là:
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho điểm M (-2;-1;3). Phương trình mặt phẳng đi qua các điểm lần lượt là hình chiếu của điểm M lên các trục tọa độ Ox, Oy, Oz là:
![]()
![]()
![]()
![]()
Trong không gian Oxyz, cho hình hộp chữ nhật ABCD.A’B’C’D’ có đỉnh A trùng với gốc O, có
A
B
→
,
A
D
→
,
A
A
→
theo thứ tự cùng hướng với
i
→
,
j
→
,
k...
Đọc tiếp
Trong không gian Oxyz, cho hình hộp chữ nhật ABCD.A’B’C’D’ có đỉnh A trùng với gốc O, có A B → , A D → , A A ' → theo thứ tự cùng hướng với i → , j → , k → và có AB = a, AD = b, AA’ = c. Hãy tính tọa độ các vecto A B → , A C → , A C ' → v à A M → với M là trung điểm của cạnh C’D’.
Trong không gian với hệ tọa độ Oxyz, tính thể tích tứ diện OABC biết A, B, C lần lượt là giao điểm của mặt phẳng 2x-3y+4z+240 với các trục Ox, Oy, Oz. A. 288 B. 192 C. 96 D. 78
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, tính thể tích tứ diện OABC biết A, B, C lần lượt là giao điểm của mặt phẳng 2x-3y+4z+24=0 với các trục Ox, Oy, Oz.
A. 288
B. 192
C. 96
D. 78
Trong không gian tọa độ
O
;
i
→
,
j
→
,
k
→
, cho ba vecto
a
→
1
;
2
;
3
,...
Đọc tiếp
Trong không gian tọa độ O ; i → , j → , k → , cho ba vecto a → = 1 ; 2 ; 3 , b → = - 2 ; 0 ; 1 , c → = - 1 ; 0 ; 1 . Tìm tọa độ của vecto n → = a → + b → + 2 c → - 3 i →
![]()
![]()
![]()
![]()
Trong không gian với hệ trục tọa độ Oxyz, cho điểm . Gọi
A
1
,
A
2
,
A
3
lần lượt là hình chiếu vuông góc của A lên các trục Ox, Oy, Oz. Phương trình của mặt phẳng
A
1
A
2
A
3
là
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho điểm . Gọi A 1 , A 2 , A 3 lần lượt là hình chiếu vuông góc của A lên các trục Ox, Oy, Oz. Phương trình của mặt phẳng A 1 A 2 A 3 là
![]()
![]()
![]()
![]()