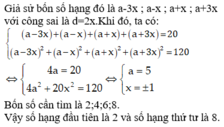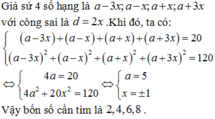Tìm 1 CSN có 4 số hạng biết tổng của chúng bằng 15 và tổng các bình phương của chúng bằng 85

Những câu hỏi liên quan
tìm 3 số hạng liên tiếp của 1 cấp số cộng biết tổng của chúng bằng 12 và tổng các bình phương của chúng bằng 66
Lời giải:
Gọi số hạng đầu tiên là $a$ và công sai $d$. Khi đó số hạng thứ 2 và 3 lần lượt là $a+d, a+2d$
Theo bài ra ta có:
$a+(a+d)+(a+2d)=12$
$\Rightarrow a+d=4$
$a^2+(a+d)^2+(a+2d)^2=66$
$\Leftrightarrow 3a^2+5d^2+6ad=66$
$\Leftrightarrow 3(4-d)^2+5d^2+6(4-d)d=66$
$\Leftrightarrow 2d^2-18=0$
$\Leftrightarrow d=\pm 3$
Nếu $d=3$ thì $a=1$. Khi đó 3 số cần tìm là $1,4, 7$
Nếu $d=-3$ thì $a=7$. Khi đó 3 số cần tìm là $7, 4, 1$
Đúng 0
Bình luận (0)
\(S_3=\dfrac{3\left[2u_1+2d\right]}{2}\)
\(\Leftrightarrow2u_1+2d=\dfrac{2S_3}{3}\)
\(\Leftrightarrow2\left(u_1+d\right)=\dfrac{2S_3}{3}\)
\(\Leftrightarrow u_1+d=\dfrac{S_3}{3}=\dfrac{12}{3}=4\)
\(\Rightarrow\left\{{}\begin{matrix}u_1=1\\d=3\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}u_2=4\\u_3=7\end{matrix}\right.\)
mà \(u_1^2+u_2^2+u_3^2=1^2+4^2+7^2=66\) (thỏa đề bài)
Vậy 3 số hạng liên tiếp của 1 cấp số cộng là : \(1;4;7\)
Đúng 0
Bình luận (0)
Bốn số hạng liên tiếp của một cấp số cộng biết tổng của chúng bằng 20 và tổng các bình phương của chúng bằng 120. Tìm số hạng đầu tiên và số hạng thứ tư của dãy ? A. 1;7 B. 2;8 C.2;10 D.3;9
Đọc tiếp
Bốn số hạng liên tiếp của một cấp số cộng biết tổng của chúng bằng 20 và tổng các bình phương của chúng bằng 120. Tìm số hạng đầu tiên và số hạng thứ tư của dãy ?
A. 1;7
B. 2;8
C.2;10
D.3;9
Tìm bốn số hạng liên tiếp của một cấp số cộng biết tổng của chúng bằng 20 và tổng các bình phương của chúng bằng 120. A. 1,5,6,8 B. 2,4,6,8 C. 1,4,6,9 D. 1,4,7,8
Đọc tiếp
Tìm bốn số hạng liên tiếp của một cấp số cộng biết tổng của chúng bằng 20 và tổng các bình phương của chúng bằng 120.
A. 1,5,6,8
B. 2,4,6,8
C. 1,4,6,9
D. 1,4,7,8
Bốn số hạng liên tiếp của một cấp số cộng biết tổng của chúng bằng 20 và tổng các bình phương của chúng bằng 120. Tính tổng của hai số hạng đầu tiên?
A. 6
B. 7
C. 5
D. 8
Chọn A
Giả sử bốn số hạng đó là a − 3 x ; a − x ; a + x ; a + 3 x với công sai là d =2x. Khi đó, ta có:
a − 3 x + a − x + a + x + a + 3 x = 20 a − 3 x 2 + a − x 2 + a + x 2 + a + 3 x 2 = 120
⇔ 4 a = 20 4 a 2 + 20 x 2 = 120 ⇔ a = 5 x = ± 1
Vậy bốn số cần tìm là 2; 4; 6; 8.
Tổng của 2 số hạng đầu tiên là: 2+ 4= 6.
Đúng 0
Bình luận (0)
Ba số hạng liên tiếp của một cấp số cộng có tổng bằng -9 và tổng các bình phương của chúng bằng 29. Tìm số hạng đầu tiên
A. -3 hoặc – 6
B. – 4 hoặc -2
C. -1 hoặc -5
D. -4 hoặc - 7
Chọn B
Gọi ba số hạng liên tiếp của cấp số cộng là a - 2x; a ; a+2x với công sai d=2x.
Theo giả thiết ta có:
a − 2 x + a + a + 2 x = − 9 ( a - 2 x ) 2 + a 2 + a + 2 x 2 = 29 ⇔ 3 a = − 9 3 a 2 + 8 x 2 = 29 ⇔ a = − 3 8 x 2 = 2 ⇔ a = − 3 x = ± 1 2
với
x = 1 2 ⇒ u 1 = a − 2 x = − 3 − 2. 1 2 = − 4
với
x = − 1 2 ⇒ u 1 = a − 2 x = − 3 − 2. − 1 2 = − 2
Vậy số hạng đầu tiên là -4 hoặc -2
Đúng 0
Bình luận (0)
Tìm một cấp số cộng tăng, biết rằng tổng ba số hạng đầu của nó bằng 27 và tổng các bình phương của chúng bằng 275.
Gọi công sai của cấp số cộng là d; số hạng đầu là u1 = x - d, u2 = x, u3 = x + d.
CSC tăng nên d > 0.
Theo giả thiết, ta có hệ:
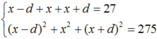
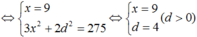
Vậy cấp số cộng cần tìm là : 5, 9, 13 .
Đúng 0
Bình luận (0)
Cho bốn số hạng liên tiếp của một cấp số cộng, có tổng của chúng bằng 16 và tổng bình phương của chúng bằng 84. Tính tổng hai bình phương số hạng đầu và số hạng cuối của bốn số hạng đó. A. 34 B. 64 C. 50 D. 49
Đọc tiếp
Cho bốn số hạng liên tiếp của một cấp số cộng, có tổng của chúng bằng 16 và tổng bình phương của chúng bằng 84. Tính tổng hai bình phương số hạng đầu và số hạng cuối của bốn số hạng đó.
A. 34
B. 64
C. 50
D. 49
Đáp án C
Gọi d = 2 x là công sai
ta có bốn số là a - 3 x , a - x , a + x , a + 3 x
Khi đó, từ giả thiết ta có:
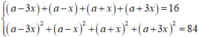
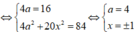
⇔ 1 , 3 , 5 , 7 7 , 5 , 3 , 1
Tổng bình phương của số hạng đầu và cuối là 1 2 + 7 2 = 50
Đúng 0
Bình luận (0)
Cho bốn số hạng liên tiếp của một cấp số cộng, có tổng của chúng bằng 16 và tổng bình phương của chúng bằng 84. Tính tổng hai bình phương số hạng đầu và số hạng cuối của bốn số hạng đó.
A. 34
B. 64
C. 50
D. 49
Đáp án C.

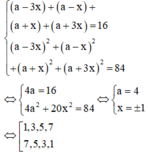
Tổng bình phương của số hạng đầu và cuối là 1 2 + 7 2 = 50
Đúng 0
Bình luận (0)
Cho bốn số hạng liên tiếp của một cấp số cộng, có tổng của chúng bằng 16 và tổng bình phương của chúng bằng 84. Tính tổng hai bình phương số hạng đầu và số hạng cuối của bốn số hạng đó.
A. 49
B. 64
C. 50
D. 34