Cho tam giác DEF vuông tại D đường cao DK cho biết DK=12cm, KE=9cm. Tính KF? DE? DF?

Những câu hỏi liên quan
cho tam giác DEF có DK là tia phân giác của góc D, DF=9cm, DE=27cm. tính tỉ số KE/KF. tính KE biết KF=6cm
Xét ΔDEF có DK là đường phân giác ứng với cạnh EF(gt)
nên \(\dfrac{KE}{KF}=\dfrac{DE}{DF}\)(Tính chất đường phân giác của tam giác)
\(\Leftrightarrow\dfrac{KE}{KF}=\dfrac{27}{9}=3\)
Đúng 1
Bình luận (0)
Ta có: \(\dfrac{KE}{KF}=3\)(cmt)
\(\Leftrightarrow KE=3\cdot KF=3\cdot6=18\left(cm\right)\)
Vậy: KE=18cm
Đúng 1
Bình luận (0)
+, ta có tam giác DK là tia pg của góc EDF
=> EK/KF= DE/DF
=> EK/FK= 27/9= 3
+, có EK/DE=KF/DF=> KE= 18cm
Đúng 1
Bình luận (0)
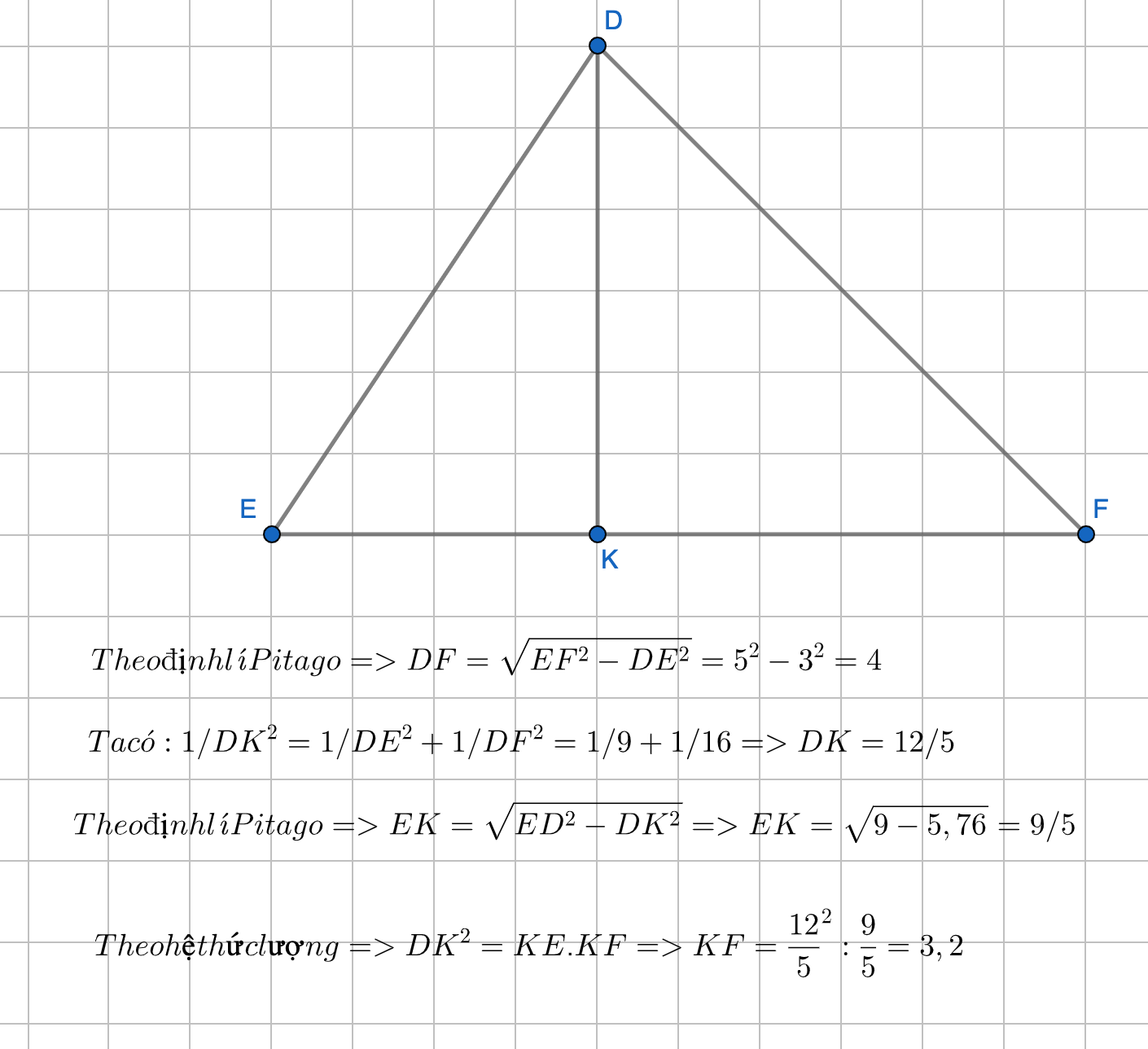
Cho tam giác DEF vuông tại D , có đường cao DK ; DE = 3cm , EF = 5cm . Tính EK , KF , DK.
Áp dụng định lí Pytago vào ΔDEF vuông tại D, ta được:
\(DE^2+DF^2=EF^2\)
\(\Leftrightarrow DF^2=5^2-3^2=16\)
hay DE=4(cm)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔDEF vuông tại D có DK là đường cao ứng với cạnh huyền EF, ta được:
\(DK\cdot FE=DE\cdot DF\)
\(\Leftrightarrow DK\cdot5=3\cdot4=12\)
hay DK=2,4(cm)
Áp dụng định lí Pytago vào ΔDKE vuông tại K, ta được:
\(DE^2=DK^2+EK^2\)
\(\Leftrightarrow EK^2=3^2-2.4^2=3.24\)
hay EK=1,8(cm)
Ta có: EK+FK=EF(K nằm giữa E và F)
nên FK=5-1,8=3,2(cm)
Đúng 3
Bình luận (0)
Áp dụng hệ thức lượng:
\(DE^2=EK.EF\Rightarrow EK=\dfrac{DE^2}{EF}=1,8\left(cm\right)\)
\(KF=EF-EK=3,2\left(cm\right)\)
\(DK^2=EK.KF\Rightarrow DK=\sqrt{EK.KF}=2,4\left(cm\right)\)
Đúng 2
Bình luận (0)
Cho tam giác DEF có 3 góc vuông.Vẽ đường cao DK.Biết DE=12cm,DK=6cm,KF=8cm.Từ K kẻ KH vuông góc với DF tại H,KI vuông góc DE tại I.
a)Tính DI,EI và số đo góc DFK
b)Chứng minh:DI.DE=DH.DF
c)Tính diện tích tam giác DIH
Cho tam giác DEF vuông tại D có DE= 6cm, DF= 8 cm, đường cao DH. Đường phân giác EK cắt DH tại I ( K thuộc DF) a) Tính độ dài EF, DK, KF. b) Chứng minh tam giác DEF đồng dạng tam giác HEI => DE. EI= EK. EH c) Gọi G là trung điểm của IK. Chứng minh DG vuông góc với IK
a: \(EF=\sqrt{6^2+8^2}=10\left(cm\right)\)
Xet ΔEDF có EK là phân giác
nên DK/DE=FK/FE
=>DK/3=FK/5=(DK+FK)/(3+5)=8/8=1
=>DK=3cm; FK=5cm
b: Xet ΔDEK vuông tại D và ΔHEI vuông tại H có
góc DEK=góc HEI
=>ΔDEK đồng dạng với ΔHEI
=>ED/EH=EK/EI
=>ED*EI=EK*EH
c: góc DKI=90 độ-góc KED
góc DIK=góc HIE=90 độ-góc KEF
mà góc KED=góc KEF
nên góc DKI=góc DIK
=>ΔDKI cân tại D
mà DG là trung tuyến
nên DG vuông góc IK
Đúng 0
Bình luận (1)
Cho tam giác DEF vuông tại D, đường cao DK . Cho DK = 6cm, EK= 8cm. Tính DE, DF, EF,FK
trong \(\Delta DEF\) vuông tại D có
\(DK^2=EK.KF\)(đlý)\(\Rightarrow KF=\dfrac{DK^2}{EK}=\dfrac{6^2}{8}\)=4,5
ta có:EF=EK+KF=8+4,5=12,5
\(DE^2=EF.EK\left(đlý\right)\)=12,5.8=100\(\Rightarrow DE=10\)
\(DF^2=EF.KF\)(đlý)=12,5.4,5=56,25\(\Rightarrow\)DF=7,5
Đúng 0
Bình luận (0)
Cho ∆Def vuong tại D có DE = 3cm , EF vẽ đường cao AH d k đường phân giác cy k thuộc EF được k vẽ kh vuông góc với df a tính độ dài EF chứng minh rằng tam giác DEF đồng dạng với tam giác HKF và DE.HF = DF.HK c, tính độ dài DK , KF ,KH
Đường cao AH hay DK vậy bạn?
Đúng 0
Bình luận (0)
Cho tam giác DEF vuông tại D, đường cao DK. Biết DE = 16cm, EF = 20cm
a) Chứng minh tam giác DKF đồng dạng với tam giác EDF
b) Tính độ dài các đoạn thẳng DF; DK
c) Kẻ đường phân giác FI (I thuộc DE) cắt DK tại M. \(\dfrac{MK}{MD}\) = \(\dfrac{DI}{EI}\)
a: Xét ΔDKF vuông tại K và ΔEDF vuông tại D có
góc F chung
=>ΔDKF đồng dạng với ΔEDF
b: \(DF=\sqrt{20^2-16^2}=12\left(cm\right)\)
DK=12*16/20=9,6cm
c: MK/MD=FK/FD
DI/EI=FD/FE
mà FK/FD=FD/FE
nên MK/MD=DI/EI
Đúng 1
Bình luận (0)
cho tam giác DEF vuông tại D, DK là đường cao.
a) DE mũ 2 = EK.EF
b) DF mũ 2 = FK.EF
c) DK mũ 2 = KE.KF
Hình bạn tự vẽ ạ
a,Xét \(\Delta DEF\) và \(\Delta KED\) có :
\(\widehat{EKD}=\widehat{EDF}=90^0\)
\(\widehat{E}:chung\)
\(\Rightarrow\Delta DEF\sim\Delta KED\left(g-g\right)\)
\(\Rightarrow\dfrac{DE}{EK}=\dfrac{EF}{DE}\)
\(\Rightarrow DE^2=EK.EF\)
b, Xét \(\Delta DFE\) và \(\Delta KFD\) có :
\(\widehat{FKD}=\widehat{FDE}=90^0\)
\(\widehat{F}:chung\)
\(\Rightarrow\Delta DFE\sim\Delta KFD\left(g-g\right)\)
\(\Rightarrow\dfrac{DF}{FK}=\dfrac{EF}{DF}\)
\(\Rightarrow DF^2=KK.EF\)
c, Xét \(\Delta KED\) và \(\Delta KDF\) có :
\(\widehat{EKD}=\widehat{FKD}=90^0\)
\(\widehat{E}=\widehat{KDF}\left(phụ\cdot với\cdot\widehat{F}\right)\)
\(\Rightarrow\Delta KED\sim\Delta KDF\left(g-g\right)\)
\(\Rightarrow\dfrac{DK}{KE}=\dfrac{KF}{DK}\)
\(\Rightarrow DK^2=KE.KF\)
Đúng 1
Bình luận (0)
Cho tam giác DEF vuông tại D, đường cao DH. Gọi I. K lần lượt là hình chiếu của điểm H trên các cạnh DE và DF. Biết FH = 4cm, HE = 9cm.
a, Tính DE, DF, IK
b, Chứng minh: DI . DE = DK . DF
c, Gọi M, N lần lượt là trung điểm của HE và HF. Tính diện tích tứ giác IKMN.
...............................................................................
..........................................................................................
...........................................................................tgbvn JGKGITJNNFJFJNFJBFÒNBFOHRJ;FFJh' IIIor ỉie
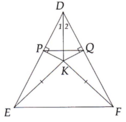
Cho tam giác DEF có DE = DF. Lấy điểm K nằm trong tam giác sao cho KE = KF. Kẻ KP vuông góc với DE (P thuộc DE), KQ vuông góc với DF (Q thuộc DF). Chứng minh:
a) K thuộc đường trung trực của EF và PQ;
b) DK là đường trung trực của EF và PQ. Từ đó suy ra PQ//EF.