Đáp án:

AD+BC

=ED-EA+EC-EB

=(ED+EC)-(EA+EB) (1)

Mà E là trung điểm của AB=> EA+EB=0

(1)=2EF (F là trung điểm DC)

E trên trục hoành nên E(x;0)

A(6;3); B(-3;6); E(x;0)

\(\overrightarrow{AB}=\left(-9;3\right);\overrightarrow{AE}=\left(x-6;-3\right)\)

Để A,B,E thẳng hàng thì \(\dfrac{x-6}{-9}=\dfrac{-3}{3}=-1\)

=>x-6=9

=>x=15

Vậy: E(15;0)

Do E thuộc trục hoành nên tọa độ có dạng \(E\left(x;0\right)\)

\(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AB}=\left(-9;3\right)\\\overrightarrow{AE}=\left(x-6;-3\right)\end{matrix}\right.\)

3 điểm A, B, E thẳng hàng khi:

\(\dfrac{x-6}{-9}=\dfrac{-3}{3}\Rightarrow x-6=9\)

\(\Rightarrow x=15\Rightarrow E\left(15;0\right)\)

0

a) Ta có {AB⊥ADAB⊥SA⇒AB⊥(SAD)⇒(SAB)⊥(SAD){AB⊥ADAB⊥SA⇒AB⊥(SAD)⇒(SAB)⊥(SAD).

b) Ta có {BC⊥ABBC⊥SA⇒BC⊥(SAB){BC⊥ABBC⊥SA⇒BC⊥(SAB).

Suy ra góc giữa SCSC và (SAB)(SAB) là góc ˆCSBCSB^.

Xét tam giác SABSAB vuông tại AA có SB=√AB2+SA2=a√3SB=AB2+SA2=a3. tanˆCSB=CBSB=aa√3=1√3⇒ˆCSB=30∘tan⁡CSB^=CBSB=aa3=13⇒CSB^=30∘.

Vậy ˆ(SC,(SAB))=30∘(SC,(SAB))^=30∘

c) Gọi MMlà trung điểm ADAD.

Suy ra ABCMABCM là hình vuông và CM=AB=aCM=AB=a.

Suy ra CM=12ADCM=12AD nên ΔACDΔACD vuông tại CC hay AC⊥CDAC⊥CD.

Ta có {CD⊥ACCD⊥SA⇒CD⊥(SAC){CD⊥ACCD⊥SA⇒CD⊥(SAC).

Kẻ AK⊥SC (K∈SC)AK⊥SC (K∈SC)

⇒AK⊥(SCD)⇒d(A,(SCD))=AK⇒AK⊥(SCD)⇒d(A,(SCD))=AK.

AC=√AB2+BC2=a√2AC=AB2+BC2=a2.

Do đó d(A,(SCD))=AK=SA.AC√SA2+AC2=ad(A,(SCD))=AK=SA.ACSA2+AC2=a. (∗)(∗)

Trong (ABCD)(ABCD), gọi {E}=AB∩CD{E}=AB∩CD.

Ta có ⎧⎨⎩BC//ADBC=12AD{BC//ADBC=12AD nên BCBC là đường trung bình của ΔEADΔEAD.

⇒SB⇒SB là đường trung tuyến của ΔSAEΔSAE. (1)(1)

Mặt khác, tam giác ΔSAEΔSAE vuông tại AA có chiều cao AHAH cho ta SH.SB=SA2 ⇒ SHSB=SA2SB2=23SH.SB=SA2 ⇒ SHSB=SA2SB2=23 (2)(2)

Từ (1)(1) và (2)(2) suy ra HH là trọng tâm tam giác ΔSAEΔSAE.

Trong (SAE)(SAE), gọi {L}=AH∩SE⇒⎧⎨⎩AH∩(SCD)={L}LHLA=13{L}=AH∩SE⇒{AH∩(SCD)={L}LHLA=13.

⇒d(H,(SCD))d(A,(SCD))=LHLA=13 (∗∗)⇒d(H,(SCD))d(A,(SCD))=LHLA=13 (∗∗).

Từ (∗)(∗) và (∗∗)(∗∗) suy ra d(H,(SCD))=a3d(H,(SCD))=a3.

mu

Goi 3 canh cua tam giac la a,b,c . Goi a bang x

ta co :

4a/2=12b/2=xc/2=S

suy ra a=2 ; b=6 ; 2S/x. Do x-y [bat dang thuc trong tam giac]

suy ra S/2-S/6<2S ma x<2S/3.Ma x thuoc Z

suy ra x=4,5

{CAU 2 } xet thay h 4 so la so am

suy ra co 1 hoac 3 so la so am trong h do

xet tung truong hop ta co:

+ co 1 so am

[x mu 2] - 10< [x mu 2] -7 suy ra [x mu 2] - 10 <0 < [x mu hai] -7

suy ra 7<[x mu2]<10 suy ra [x mu 2] = 9 suy ra x= 3 hoac -3 

+co 3 so am 1 so duong 

[x mu 2] - 4<[x mu 2 ] -1 <[ x mu 2] <4

suy ra khong co gia tri thoa man

Vay x=3;-3

anh lam song roi day ny

Câu 2: pt đã cho \(\Leftrightarrow x^3-3x^2+3x-1+x^3+x^3+3x^2+3x+1=x^3+6x^2+12x+8\)

\(\Leftrightarrow2x^3-6x^2-6x-8=0\)

\(\Leftrightarrow x^2-3x^2-3x-4=0\)

\(\Leftrightarrow\left(x-1\right)^3-6\left(x-1\right)-9=0\) (*)

Đặt  \(x-1=t\) thì (*) trở thành \(t^3-6t-9=0\) 

\(\Leftrightarrow t^3-9t+3t-9=0\)

\(\Leftrightarrow t\left(t^2-9\right)+3\left(t-3\right)=0\)

\(\Leftrightarrow\left(t-3\right)\left(t^2+3t\right)+3\left(t-3\right)=0\)

\(\Leftrightarrow\left(t-3\right)\left(t^3+3t+3\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}t=3\\t^2+3t+3=0\left(loại\right)\end{matrix}\right.\)

\(\Leftrightarrow x-1=3\) 

\(\Leftrightarrow x=4\)

Vậy pt đã cho có nghiệm \(x=4\)

bài đấy thì em làm được rồi á. Chỉ là em đăng lên xem còn cách nào giải hay hơn thôi ạ...

Câu 1:

\(A=\left(2\sqrt{3}+4\cdot\sqrt{27}-\sqrt{108}\right):2\sqrt{3}\)

\(=\dfrac{\left(2\sqrt{3}+4\cdot3\sqrt{3}-6\sqrt{3}\right)}{2\sqrt{3}}\)

\(=\dfrac{2\sqrt{3}+12\sqrt{3}-6\sqrt{3}}{2\sqrt{3}}=\dfrac{8\sqrt{3}}{2\sqrt{3}}=4\)

\(B=\sqrt{9+4\sqrt{5}}-2\left(\sqrt{5}+1\right)\)

\(=\sqrt{5+2\cdot\sqrt{5}\cdot2+4}-2\left(\sqrt{5}+1\right)\)

\(=\sqrt{\left(\sqrt{5}+2\right)^2}-2\left(\sqrt{5}+1\right)\)

\(=\sqrt{5}+2-2\sqrt{5}-2=-\sqrt{5}\)

Câu 2:

a: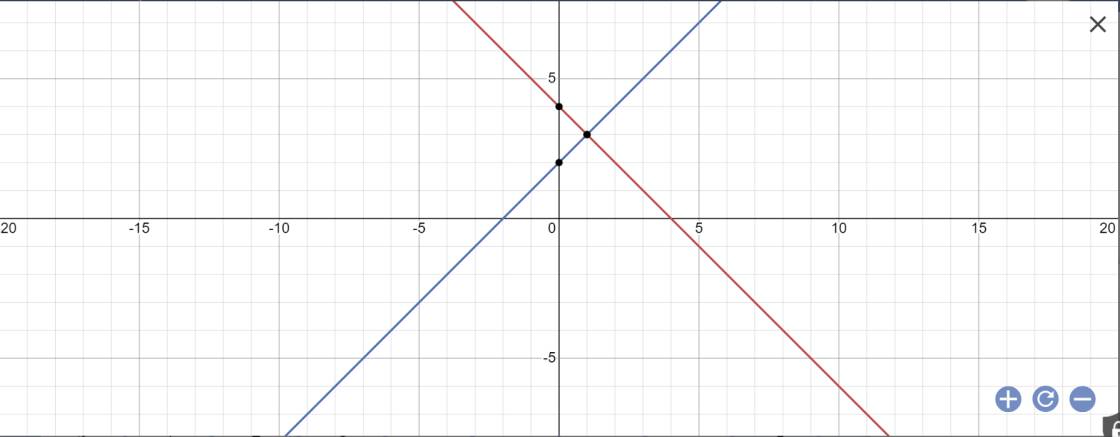 

b: Tọa độ giao điểm của (d1) và (d2) là:

\(\left\{{}\begin{matrix}x+2=-x+4\\y=x+2\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}2x=2\\y=x+2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=1+2=3\end{matrix}\right.\)

Thay x=1 và y=3 vào (d3), ta được:

\(m\cdot1+m=3\)

=>2m=3

=>\(m=\dfrac{3}{2}\)

Câu 4:

a: Xét (O) có

ΔCAB nội tiếp

AB là đường kính

Do đó: ΔCAB vuông tại C

Xét tứ giác CMON có \(\widehat{CMO}=\widehat{CNO}=\widehat{MCN}=90^0\)

=>CMON là hình chữ nhật

b: Ta có: ΔCAB vuông tại C

=>CA\(\perp\)CB tại C

=>AC\(\perp\)EB tại C

Xét ΔAEB vuông tại A có AC là đường cao

nên \(EC\cdot CB=AC^2\left(1\right)\)

Xét ΔCAB vuông tại C có CH là đường cao

nên \(AH\cdot AB=AC^2\left(2\right)\)

Từ (1) và (2) suy ra \(EC\cdot CB=AH\cdot AB\)

c: Ta có: ΔOAC cân tại O

mà OM là đường cao

nên OM là phân giác của góc AOC

Xét ΔOAI và ΔOCI có

OA=OC

\(\widehat{AOI}=\widehat{COI}\)

OI chung

Do đó: ΔOAI=ΔOCI

=>\(\widehat{OAI}=\widehat{OCI}=90^0\)

Ta có: ΔOBC cân tại O

mà ON là đường cao

nên ON là phân giác của góc COB

Xét ΔOBF và ΔOCF có

OB=OC

\(\widehat{BOF}=\widehat{COF}\)

OF chung

Do đó: ΔOBF=ΔOCF

=>\(\widehat{OBF}=\widehat{OCF}=90^0\)

Ta có: \(\widehat{ICF}=\widehat{ICO}+\widehat{FCO}\)

\(=90^0+90^0=180^0\)

=>I,C,F thẳng hàng

=>OC\(\perp\)IF tại C

Xét (O) có

OC là bán kính

IF\(\perp\)OC tại O

Do đó: IF là tiếp tuyến của (O)

\(\overrightarrow{AB}=\left(4;4\right);\overrightarrow{AE}=\left(a+1;b+2\right)\) mà E di động trên đường thẳng AB nên A,B,E thẳng hàng tương đương với \(\dfrac{a+1}{4}=\dfrac{b+2}{4}\) <=> \(a=b+1\).Vậy E(b+1;b)

Đặt \(\overrightarrow{u}=2\overrightarrow{EA}+3\overrightarrow{EB}-\overrightarrow{EC}\) => \(\overrightarrow{u}=\left(-1-4b;3-4b\right)\)

có : \(\left|2\overrightarrow{EA}+3\overrightarrow{EB}-\overrightarrow{EC}\right|=\left|\overrightarrow{u}\right|=\sqrt{\left(-1-4b\right)^2+\left(3-4b^2\right)}\)

Đặt : 1-4b = t => \(\left\{{}\begin{matrix}-1-4b=t-2\\3-4b=t+2\end{matrix}\right.\) khi đó \(\left|\overrightarrow{u}\right|=\sqrt{\left(t-2\right)^2+\left(t+2\right)^2}=\sqrt{2t^2+8}\ge2\sqrt{2}\)

\(\left|2\overrightarrow{EA}+3\overrightarrow{EB}-\overrightarrow{EC}\right|\)đạt GTNN khi và chỉ khi t =0 <=> b=1/4 => a=5/4

vậy \(a^2-b^2=\dfrac{3}{2}\)

Chọn D