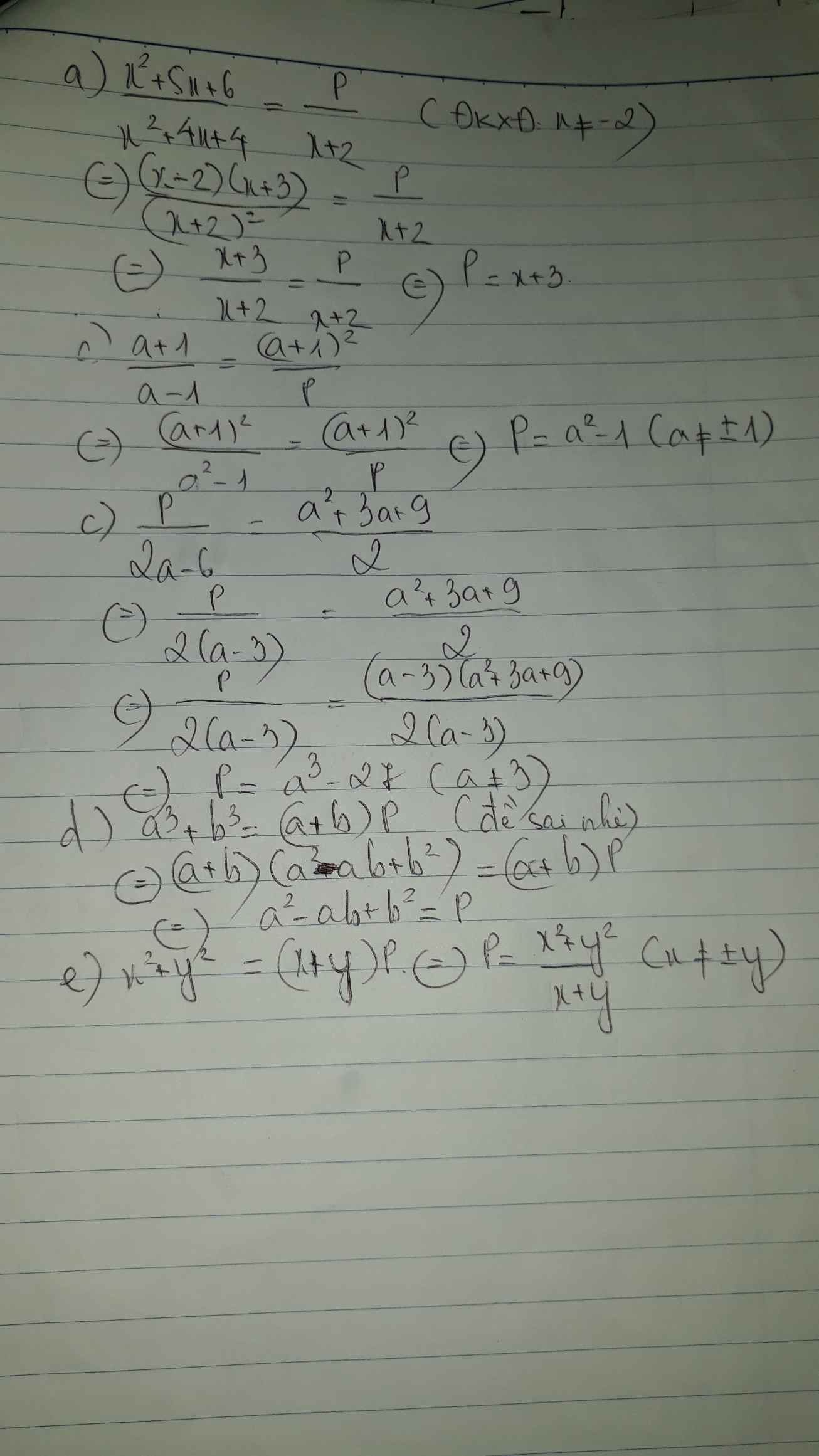cho đa thức D(x)-x2+ax.Biết D(-1)=2D (1) . Tìm a

Những câu hỏi liên quan
Cho đa thức D(x)=3x2 +ax.Biết D(2)=4D(1).Tìm a?
D(2) = 4D (1)
<=>3*2^2 + a*2 = 4 (3*1^2 + a * 1)
<=> a = 0
Đúng 0
Bình luận (0)
Cho đa thức A = x4 + x3 – 2x – 2
a) Tìm đa thức B sao cho A + B = x3 + 3x + 1
b) Tìm đa thức C sao cho A – C = x5
c) Tìm đa thức D biết rằng D = (2x2 – 3) . A
d) Tìm đa thức P sao cho A = (x+1) . P
e) Có hay không một đa thức Q sao cho A = (x2 + 1) . Q?
a) Ta có:
B = (A + B) – A
= (x3 + 3x + 1) – (x4 + x3 – 2x – 2)
= x3 + 3x + 1 – x4 - x3 + 2x + 2
= – x4 + (x3 – x3) + (3x + 2x) + (1 + 2)
= – x4 + 5x + 3.
b) C = A - (A – C)
= x4 + x3 – 2x – 2 – x5
= – x5 + x4 + x3 – 2x – 2.
c) D = (2x2 – 3) . A
= (2x2 – 3) . (x4 + x3 – 2x – 2)
= 2x2 . (x4 + x3 – 2x – 2) + (-3) .(x4 + x3 – 2x – 2)
= 2x2 . x4 + 2x2 . x3 + 2x2 . (-2x) + 2x2 . (-2) + (-3). x4 + (-3) . x3 + (-3). (-2x) + (-3). (-2)
= 2x6 + 2x5 – 4x3 – 4x2 – 3x4 – 3x3 + 6x + 6
= 2x6 + 2x5 – 3x4 + (-4x3 – 3x3) – 4x2+ 6x + 6
= 2x6 + 2x5 – 3x4 – 7x3 – 4x2+ 6x + 6.
d) P = A : (x+1) = (x4 + x3 – 2x – 2) : (x + 1)
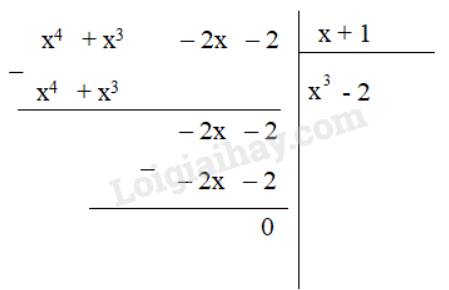
Vậy P = x3 - 2
e) Q = A : (x2 + 1)
Nếu A chia cho đa thức x2 + 1 không dư thì có một đa thức Q thỏa mãn
Ta thực hiện phép chia (x4 + x3 – 2x – 2) : (x2 + 1)
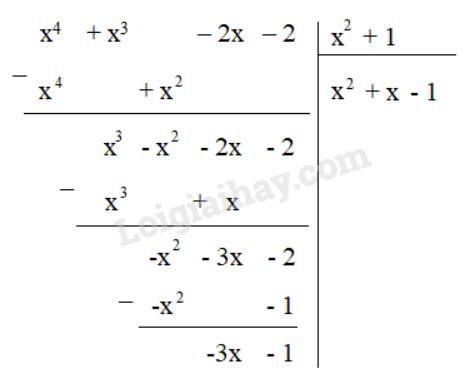
Do phép chia có dư nên không tồn tại đa thức Q thỏa mãn
Đúng 1
Bình luận (0)
Bài 2: Tìm đa thức P biết
a)x2+5x+6/x2+4x+4=P/x+2
b)a+1/a-1=(a+1)2/P
c)P/2a-6=a2+3a+9/2
d)a3+b3=(a-b).P
e)x2+y2=(x+y).P
a) Ta có: \(\dfrac{P}{x+2}=\dfrac{x^2+5x+6}{x^2+4x+4}\)
\(\Leftrightarrow\dfrac{P}{x+2}=\dfrac{\left(x+2\right)\left(x+3\right)}{\left(x+2\right)^2}=\dfrac{x+3}{x+2}\)
hay P=x+3
Đúng 1
Bình luận (0)
b) Ta có: \(\dfrac{\left(a+1\right)^2}{P}=\dfrac{a+1}{a-1}\)
\(\Leftrightarrow P=\left(a+1\right)\left(a-1\right)\)
\(\Leftrightarrow P=a^2-1\)
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
Cho đa thức A (x) =ax3+bx2+cx+d ( a khác 0)
a) Tìm giá trị a, b, c, d, để A (x) có nghiệm 1 và -1
b) Tìm nghiện thứ 3 còn lại của đa thức đó
c) Xác định các giá trị của a, b, c, d để đa thức A(x) đồng nhất với đa thức
B(x)=3x3-9x+6x2-(5bx2-3x+1)+2ax3-2d
cho đa thức A(x)=ax^3+bx^3+cx+d (a khác). Xác định các giá trị của a, b, c, d để đa thức A(x) đồng nhất với đa thức B(x)=3x^3-9x+6x^2-(5bx^2-3x+1)+2ax^3-2d
1 Tìm nghiệm các đa thức sau :
a, A[x] = x^2 + 9
b, B[x] = x^2 - 9
c,C[x] = 2x^2 - 2
d, D[x] = 3x - 6
a/\(x^2+9=0\)
\(\Rightarrow x^2=-9\)(Vô lí vì \(x^2\ge0\))
Do đó A(x) vô nghiệm
b/\(x^2-9=0\)
\(\Rightarrow x^2=9\)
\(\Rightarrow\left[{}\begin{matrix}x=3\\x=-3\end{matrix}\right.\)
Vậy nghiệm của B(x) là \(x\in\left\{3;-3\right\}\)
c/\(2x^2-2=0\)
\(\Rightarrow2x^2=2\)
\(\Rightarrow x^2=1\)
\(\Rightarrow\left[{}\begin{matrix}x=1\\x=-1\end{matrix}\right.\)
Vậy nghiệm của C(x) là \(x\in\left\{1;-1\right\}\)
d/\(3x-6=0\)
\(\Rightarrow3x=6\)
\(\Rightarrow x=2\)
Vậy nghiệm của D(x) là \(x=2\)
Đúng 1
Bình luận (0)
a: A(x)=0
=>x^2=-9(loại)
b: x^2-9=0
=>x^2=9
=>x=3 hoặc x=-3
c:2x^2-2=0
=>x^2-1=0
=>x=1 hoặc x=-1
d: 3x-6=0
=>3x=6
=>x=2
Đúng 0
Bình luận (0)
Ví dụ 1 (30s): Cho đa thức f(x) = (2x + 1)(x
2 − x + 1). Kết quả của phép chia đa thức f(x)
cho đa thức 2x + 1 là:
A. x
2 + x + 1 B. x
2 − x C. x
2 − x + 1 D. x
2 + 1
\(\dfrac{f\left(x\right)}{2x+1}=\dfrac{\left(2x+1\right)\left(x^2-x+1\right)}{2x+1}=x^2-x+1\)
Đúng 2
Bình luận (1)
Chọn C:
\(\dfrac{\left(2x+1\right)\left(x^2-x+1\right)}{2x+1}=x^2-x+1\)
Đúng 2
Bình luận (0)
ài 6.Cho 2 đa thức: C(x) 2x3 -x + 7 - x3 + 3x2 - 1 ; D(x) - x3 - 8- x2 + 2x - x2 + 2 a) Thu gọn và sắp xếp các hạng tử của mỗi đa thức theo lũy thừa giảm dần của biến. b) Tìm bậc của C(x) và hệ số tự do của D(x) c) Tính C (2); D(- 1) d) Tính C(x) + D(x); C(x) - D (x) e) Tìm x biết C(x) - D (x)
Đọc tiếp
ài 6.Cho 2 đa thức: C(x) = 2x3 -x + 7 - x3 + 3x2 - 1 ; D(x) = - x3 - 8- x2 + 2x - x2 + 2
a) Thu gọn và sắp xếp các hạng tử của mỗi đa thức theo lũy thừa giảm dần của biến.
b) Tìm bậc của C(x) và hệ số tự do của D(x) c) Tính C (2); D(- 1)
d) Tính C(x) + D(x); C(x) - D (x) e) Tìm x biết C(x) = - D (x)
a: \(C\left(x\right)=x^3+3x^2-x+6\)
\(D\left(x\right)=-x^3-2x^2+2x-6\)
b: Bậc của C(x) là 3
Hệ số tự do của D(x) là -6
c: \(C\left(2\right)=8+3\cdot4-2+6=20-2+6=24\)
d: \(C\left(x\right)+D\left(x\right)=x^2+x\)
Đúng 2
Bình luận (0)
a.
b. Bậc của C(x) là 3
Hệ số tự do của D(x) là -6
c.
d.
Đúng 0
Bình luận (0)
b) Thực hiện phép chia đa thức (2x4 – 5x3 + 2x2 +2x - 1) cho đa thức (x2 – x - 1)
Bài 2:
a) Tìm a để đa thức (2x4 + x3 - 3x2 + 5x + a) chia hết cho đa thức (x2 - x +1)
b) Tìm a để đa thức x^4 - x^3 + 6x^2 chia hết cho đa thức x^2 - x + 5
b: \(=\dfrac{2x^4-2x^3-2x^2-3x^3+3x^2+3x+x^2-x-1}{x^2-x-1}\)
\(=2x^2-3x+1\)
Đúng 0
Bình luận (0)