Cho mình hỏi bài 4 ạ. Cảm ơn 

Những câu hỏi liên quan
Cho mình hỏi bài 16,17 với ạ .mình cảm ơn
Cho mình hỏi vài bài toán này với ạ, mình đang cần gấp, cảm ơn các bạn nhiều!
3.
Do M là trung điểm BC \(\Rightarrow\overrightarrow{CM}=\dfrac{1}{2}\overrightarrow{CB}\)
N là trung điểm AC \(\Rightarrow\overrightarrow{AN}=\dfrac{1}{2}\overrightarrow{AC}\)
K là trung điểm AB \(\Rightarrow\overrightarrow{BK}=\dfrac{1}{2}\overrightarrow{BA}\)
Do đó:
\(\overrightarrow{AN}+\overrightarrow{CM}-\overrightarrow{KB}=\overrightarrow{AN}+\overrightarrow{CM}+\overrightarrow{BK}=\dfrac{1}{2}\overrightarrow{AC}+\dfrac{1}{2}\overrightarrow{CB}+\dfrac{1}{2}\overrightarrow{BA}\)
\(=\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{BA}=\overrightarrow{0}\)
4.
\(\overrightarrow{BC}=\left(6;-2\right)\)
Gọi \(A'\left(x;y\right)\Rightarrow\overrightarrow{BA'}=\left(x+3;y-1\right)\)
Do A' thuộc BC \(\Rightarrow\overrightarrow{BA'}\) và \(\overrightarrow{BC}\) cùng phương
\(\Rightarrow\dfrac{x+3}{6}=\dfrac{y-1}{-2}\Rightarrow x=-3y\)
\(\Rightarrow A'\left(-3y;y\right)\Rightarrow\overrightarrow{AA'}=\left(-3y-2;y-4\right)\)
Mà AA' vuông góc BC \(\Rightarrow\overrightarrow{AA'}.\overrightarrow{BC}=0\)
\(\Rightarrow6\left(-3y-2\right)-2\left(y-4\right)=0\Rightarrow y=-\dfrac{1}{5}\)
\(\Rightarrow A'\left(\dfrac{3}{5};-\dfrac{1}{5}\right)\)
Đúng 1
Bình luận (0)
Cho mình hỏi cách giải bài này với ạ:
\(\dfrac{1}{3+0.5}+\dfrac{1}{3-0,5}\)
Mình cảm ơn!![]()
\(\dfrac{1}{3+0,5}+\dfrac{1}{3-0,5}\)
\(=\dfrac{3-0,5}{\left(3+0,5\right)\left(3-0,5\right)}+\dfrac{3+0,5}{\left(3+0,5\right)\left(3-0,5\right)}\)
\(=\dfrac{3-0,5+3+0,5}{3^2-\left(0,5\right)^2}\)
\(=\dfrac{6}{9-0,25}\)
\(=\dfrac{24}{35}\)
Đúng 2
Bình luận (1)
cho mình hỏi cách giải bài toán này ạ, Tìm a,b để phân số 36/(a.b) = a+b
cảm ơn ạ
giúp mình bài 4 với ạ! mk cảm ơn ạ!
giúp mình bài 4 với ạ mình cảm ơn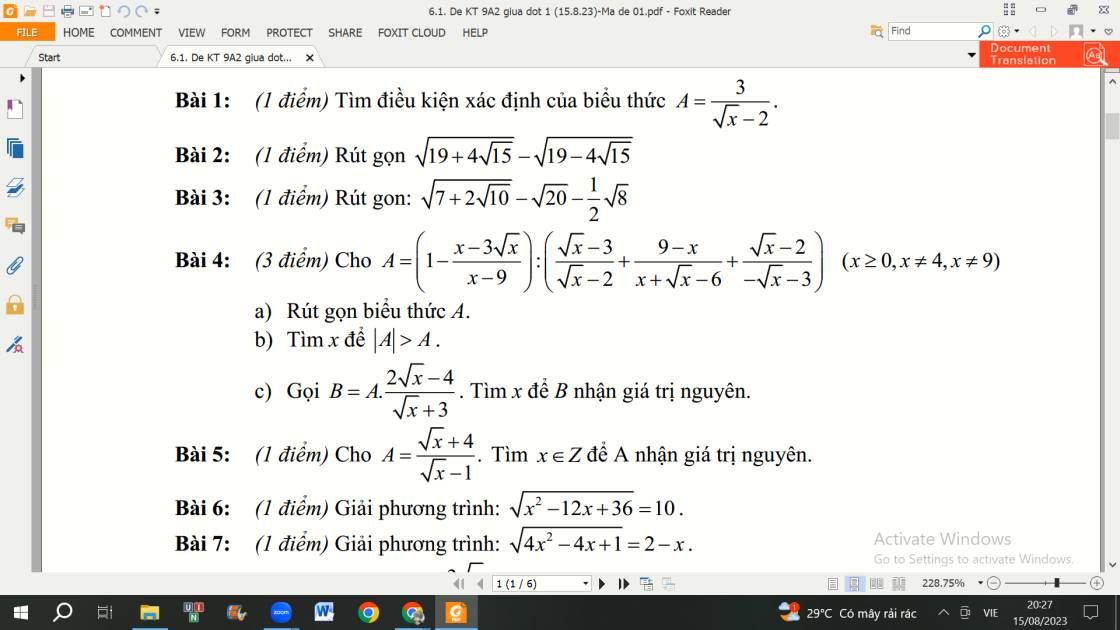
4:
a: \(A=\left(\dfrac{x-9-x+3\sqrt{x}}{x-9}\right):\left(\dfrac{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)+9-x}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+3\right)}-\dfrac{\sqrt{x}-2}{\sqrt{x}+3}\right)\)
\(=\dfrac{3\sqrt{x}-9}{x-9}:\left(\dfrac{x-9+9-x}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+3\right)}+\dfrac{-\left(\sqrt{x}-2\right)}{\sqrt{x}+3}\right)\)
\(=\dfrac{3\left(\sqrt{x}-3\right)}{x-9}\cdot\dfrac{\sqrt{x}+3}{-\left(\sqrt{x}-2\right)}=\dfrac{-3}{\sqrt{x}-2}\)
b: |A|>A
=>A<0
=>\(\dfrac{-3}{\sqrt{x}-2}< 0\)
=>căn x-2>0
=>x>4
c: \(B=\dfrac{2\left(\sqrt{x}-2\right)}{\sqrt{x}+3}\cdot\dfrac{-3}{\left(\sqrt{x}-2\right)}=\dfrac{-6}{\sqrt{x}+3}\)
Để B là số nguyên thì \(\sqrt{x}+3\inƯ\left(-6\right)\)
=>\(\sqrt{x}+3\in\left\{3;6\right\}\)
=>\(x\in\left\{0;9\right\}\)
mà x<>9
nên x=0
Đúng 1
Bình luận (0)
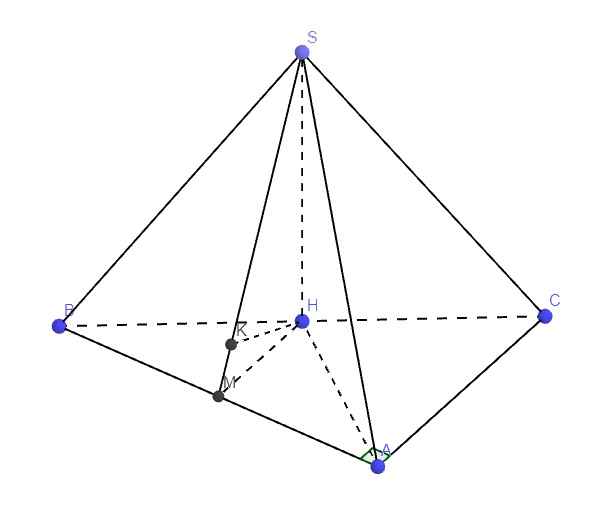
Giúp mình bài 4 với ạ mình cảm ơn
a.
\(SH\perp\left(ABC\right)\Rightarrow SH=d\left(S;\left(ABC\right)\right)\)
\(SH\perp\left(ABC\right)\Rightarrow SH\perp BC\Rightarrow\Delta SBH\) vuông tại H
\(BH=\dfrac{1}{2}BC=a\Rightarrow SH=\sqrt{SB^2-BH^2}=a\sqrt{3}\)
\(SH\perp\left(ABC\right)\Rightarrow HA\) là hình chiếu vuông góc của SA lên (ABC)
\(\Rightarrow\widehat{SAH}\) là góc giữa SA và (ABC)
\(AH=\dfrac{1}{2}BC=a\) (trung tuyến ứng với cạnh huyền)
\(\Rightarrow tan\widehat{SAH}=\dfrac{SH}{AH}=\sqrt{3}\Rightarrow\widehat{SAH}=60^0\)
b.
H là trung điểm BC, M là trung điểm AB \(\Rightarrow MH\) là đường trung bình tam giác ABC
\(\Rightarrow MH||AC\Rightarrow MH\perp AB\) (do \(AB\perp AC\))
Lại có \(SH\perp\left(ABC\right)\Rightarrow SH\perp AB\)
\(\Rightarrow AB\perp\left(SMH\right)\)
Mà \(AB=\left(SAB\right)\cap\left(ABC\right)\Rightarrow\widehat{SMH}\) là góc giữa (SAB) và (ABC)
\(AC=\sqrt{BC^2-AB^2}=a\sqrt{3}\) \(\Rightarrow MH=\dfrac{1}{2}AC=\dfrac{a\sqrt{3}}{2}\) (đường trung bình)
\(\Rightarrow tan\widehat{SMH}=\dfrac{SH}{MH}=2\Rightarrow\widehat{SMH}\approx63^023'\)
c.
Theo cmt: \(\left\{{}\begin{matrix}MH\perp SH\\MH\perp AB\end{matrix}\right.\) \(\Rightarrow MH\) là đường vuông góc chung của SH và AB
\(\Rightarrow d\left(SH;AB\right)=MH=\dfrac{a\sqrt{3}}{2}\)
Từ H kẻ HK vuông góc SM (K thuộc SM)
\(AB\perp\left(SMH\right)\Rightarrow AB\perp HK\)
\(\Rightarrow HK\perp\left(SAB\right)\Rightarrow HK=d\left(H;\left(SAB\right)\right)\)
Hệ thức lượng trong tam giác vuông SMH:
\(HK=\dfrac{SH.MH}{\sqrt{SH^2+MH^2}}=\dfrac{a\sqrt{15}}{5}\)
Đúng 0
Bình luận (0)
Giải giúp mình bài 4 ạ mình cảm ơn nhìu
Em cập nhật lại đề nha em!
Đúng 2
Bình luận (0)
Các bạn ơi cho mình hỏi nếu đề bài yêu cầu viết bài văn về một vấn đề trong đời sống thì mình viết về lòng nhân ái có được không ạ ?
Mình cảm ơn !