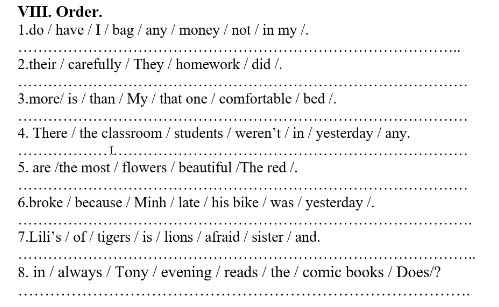
 giúp mik với mik đang cần gấp cảm ơn nhiều nha
giúp mik với mik đang cần gấp cảm ơn nhiều nha

Những câu hỏi liên quan
Mọi người giúp mik bài 1 nha mik đang cần gấp cảm ơn mọi người nhiều
giúp mik với mik đang cần gấp đó mn cảm ơn mn nhìu ạ=((



TỪ CÂU 1 ĐẾN 20 NHA Ạ CẢM ƠN NHÌU MIK ĐANG CẦN GẤP-((
1.A
2.A
3.B
4.C
5.B
6.C
7.A
8.A
9.B
10.A
11.B
12.A
13.C
14.B
15.B
16.A
17.A
18.A
19.A
20.C
Đúng 0
Bình luận (0)

LÀM GIÚP MIK VỚI MIK ĐANG CẦN GẤP Ạ
MIK CẢM ƠN RẤT NHIỀU Ạ
\(A=\dfrac{4x+2\sqrt{x}+2}{2\sqrt{x}+1}=\dfrac{2\sqrt{x}\left(2\sqrt{x}+1\right)+2}{2\sqrt{x}+1}=2\sqrt{x}+\dfrac{2}{2\sqrt{x}+1}\)
\(=2\sqrt{x}+1+\dfrac{2}{2\sqrt{x}+1}-1\ge2\sqrt{\left(2\sqrt{x}+1\right)\cdot\dfrac{2}{2\sqrt{x}+1}}-1=2\sqrt{2}-1\)
=> A \(\ge2\sqrt{2}-1\)
Dấu "=" xảy ra <=> \(2\sqrt{x}+1=\dfrac{2}{2\sqrt{x}+1}\)
<=> \(\left(2\sqrt{x}+1\right)^2=2\) <=> \(\left[{}\begin{matrix}2\sqrt{x}+1=2\\2\sqrt{x}+1=-2\left(loại\right)\end{matrix}\right.\)
<=> \(\sqrt{x}=\dfrac{1}{2}\) <=> \(x=\dfrac{1}{4}\)(tm)
Vậy minA = \(2\sqrt{2}-1\) khi x = 1/4
Đúng 1
Bình luận (0)
các bn ơi giúp mik với nha mik cảm ơn nhiều nha đag cần gấp
Đọc tiếp
các bn ơi giúp mik với nha mik cảm ơn nhiều nha đag cần gấp
a: =-5/6-3/7=-35/42-18/42=-53/42
b: =2/5-4/9=18/45-20/45=-2/45
c: =-24/35
d: =2/3x-5/4=-10/12=-5/6
Đúng 1
Bình luận (0)
Giúp mik vs ạ. Mik đang cần gấp. Mik cảm ơn nhiều
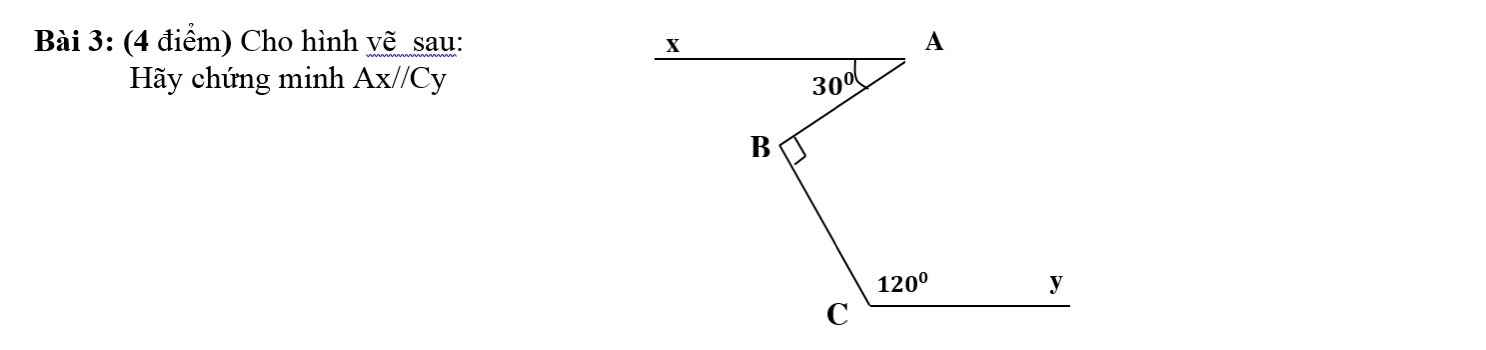
Kẻ Bz//Ax
Ta có: Ax//Bz
\(\Rightarrow\widehat{BAx}=\widehat{ABz}=30^0\)(so le trong)
\(\Rightarrow\widehat{zBC}=\widehat{ABC}-\widehat{BAx}=90^0-30^0=60^0\)
Ta có: \(\widehat{zBC}+\widehat{BCy}=60^0+120^0=180^0\)
Mà 2 góc này là 2 góc trong cùng phía
=> Bz//Cy
Mà Bz//Ax
=> Ax//Cy
Đúng 0
Bình luận (0)
Giúp mik với ạ,em đang cần gấp lắm cảm ơn mn nhiều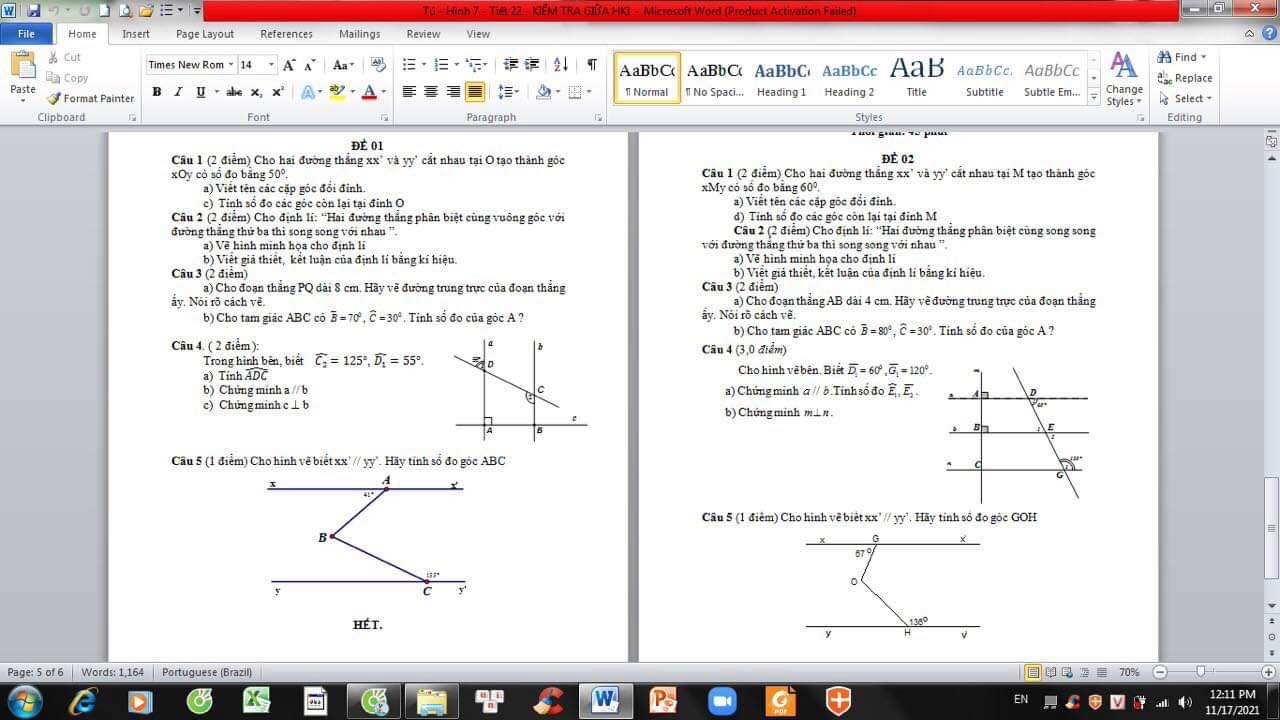
Bạn cần hỗ trợ bài nào thì nên chụp nguyên bài đó ra thôi. Nếu bạn cần giúp nhiều bài thì nên tách lẻ mỗi bài mỗi post hoặc 2 bài/ post. Bạn chụp như thế này gây "ngợp" nên sẽ ít ai dừng lại và hỗ trợ.
Đúng 0
Bình luận (0)

mn ơi giúp mik câu này với. mik đang cần gấp lắm. cảm ơn mn trc nha
em tán thành
vì Kỉ luật tạo nên sự đoàn kết, thống nhất, đảm bảo dân chủ được thực hiện một cách tốt nhất.
Có tinh thần, trách nhiệm trong học tập và công việc, luôn có ý thức vì tập thể.
Đúng 2
Bình luận (1)
mn giúp mik với,mk đang cần rất gấp ạ! Cảm ơn mn rất nhiều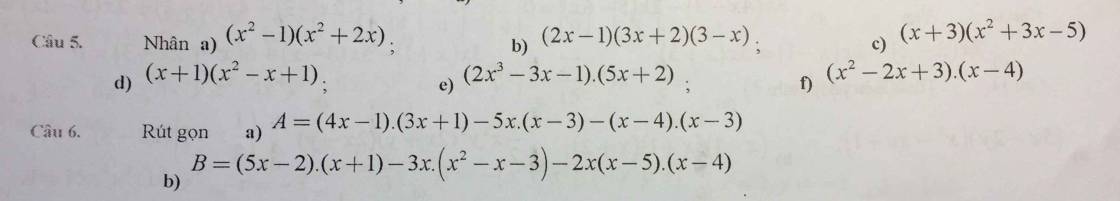
Câu 6:
a: =12x^2+4x-3x-1-5x^2+15x-x^2+7x-12
=6x^2+23x-13
b: =5x^2+5x-2x-2-3x^3+3x^2+9x-2x(x^2-9x+20)
=-3x^3+8x^2+14x-2-2x^3+18x^2-40x
=-5x^3+26x^2-26x-2
Đúng 0
Bình luận (0)
mng giúp mik bài này được ko? mik đang cần gấp . cảm ơn bạn nhiều 
a: =>x>=0 và x^2+x=x^2
=>x=0
a: =>x>=1 và 1-x^2=x^2-2x+1
=>-2x^2+2x=0 và x>=1
=>x=1
a: =>x>=1 và 1-2x^2=x^2-2x+1
=>-3x^2+2x=0 và x>=1
=>\(x\in\varnothing\)
a: ĐKXĐ: x<=2 và x^2-2x=x^2-4x+4
=>x=2
a: =>căn x^2-4=x-2
=>x>=2 và x^2-4=x^2-4x+4
=>x>=2 và 4x=8
=>x=2
b: =>x>=0 và x^2-4x+1=x^2
=>-4x+1=0 và x>=0
=>x=1/4
b: =>x>=-1 và x^2+x+1=x^2+2x+1
=>x=0
c: =>x>=1 và 4x^2-8x+1=x^2-2x+1
=>x>=1 và 3x^2-6x=0
=>x=2
b: =>x>=-1 và 5x^2-2x+2=x^2+2x+1
=>x>=-1 và 4x^2-4x+1=0
=>x=1/2
b: =>căn 4x^2-x+1=2x+3
=>x>=-3/2 và 4x^2-x+1=(2x+3)^2=4x^2+12x+9
=>x>=-3/2 và -13x=8
=>x=-8/13
Đúng 1
Bình luận (2)
1) \(\sqrt{x^2+x}=x\) (Thỏa mẵn với mọi x)
\(\Leftrightarrow x^2+x=x^2\)
\(\Leftrightarrow x^2+x-x^2=0\)
\(\Leftrightarrow x=0\)
Vậy \(x=0\)
2) \(\sqrt{1-x^2}=x-1\) (ĐK: \(x\le1\) )
\(\Leftrightarrow1-x^2=\left(x-1\right)^2\)
\(\Leftrightarrow1-x^2=x^2-2x+1\)
\(\Leftrightarrow-x^2-x^2+2x=1-1\)
\(\Leftrightarrow-2x^2+2x=0\)
\(\Leftrightarrow-2x\left(x-1\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}-2x=0\\x-1=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\left(tm\right)\\x=1\left(tm\right)\end{matrix}\right.\)
Vậy: \(S=\left\{0;1\right\}\)
\(\sqrt{1-2x^2}=x-1\) (ĐK: \(x\le\sqrt{\dfrac{1}{2}}\))
\(\Leftrightarrow1-2x^2=\left(x-1\right)^2\)
\(\Leftrightarrow1-2x^2=x^2-2x+1\)
\(\Leftrightarrow-2x^2-x^2+2x=1-1\)
\(\Leftrightarrow-3x^2+2x=0\)
\(\Leftrightarrow-x\left(3x-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}-x=0\\3x-2=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\left(tm\right)\\x=\dfrac{2}{3}\left(tm\right)\end{matrix}\right.\)
Vậy: \(S=\left\{0;\dfrac{2}{3}\right\}\)
\(\sqrt{x^2-2x}=2-x\) (ĐK: \(\left\{{}\begin{matrix}x\le0\\x\ge2\end{matrix}\right.\) )
\(\Leftrightarrow x^2-2x=\left(2-x\right)^2\)
\(\Leftrightarrow x^2-2x=4-4x+x^2\)
\(\Leftrightarrow x^2-x^2-2x+4x=4\)
\(\Leftrightarrow2x=4\)
\(\Leftrightarrow x=2\left(tm\right)\)
Vậy: \(x=2\)
\(\sqrt{x^2-4}-x+2=0\) (ĐK: \(\left\{{}\begin{matrix}x\le-2\\x\ge2\end{matrix}\right.\))
\(\Leftrightarrow\sqrt{x^2-4}=x-2\)
\(\Leftrightarrow x^2-4=\left(x-2\right)^2\)
\(\Leftrightarrow x^2-4=x^2-4x+4\)
\(\Leftrightarrow x^2-x^2+4x=4+4\)
\(\Leftrightarrow4x=8\)
\(\Leftrightarrow x=2\left(tm\right)\)
Vậy: \(x=2\)
Đúng 1
Bình luận (0)




















