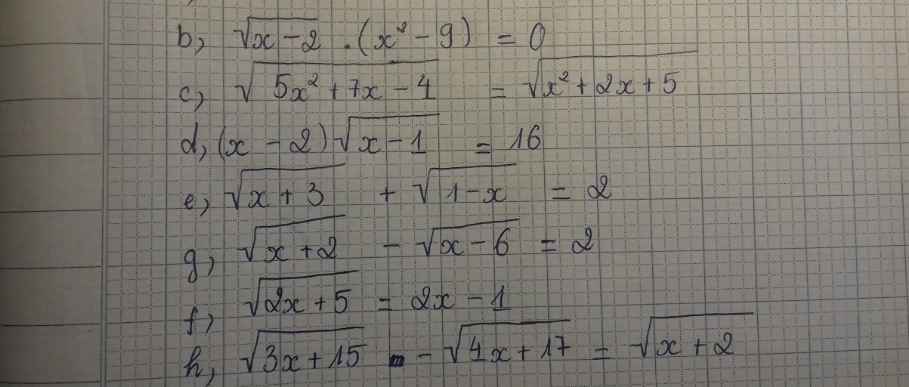a: =>x>=0 và x^2+x=x^2
=>x=0
a: =>x>=1 và 1-x^2=x^2-2x+1
=>-2x^2+2x=0 và x>=1
=>x=1
a: =>x>=1 và 1-2x^2=x^2-2x+1
=>-3x^2+2x=0 và x>=1
=>\(x\in\varnothing\)
a: ĐKXĐ: x<=2 và x^2-2x=x^2-4x+4
=>x=2
a: =>căn x^2-4=x-2
=>x>=2 và x^2-4=x^2-4x+4
=>x>=2 và 4x=8
=>x=2
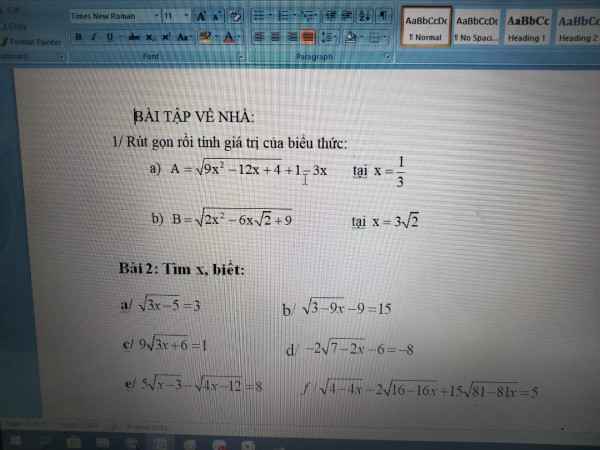
b: =>x>=0 và x^2-4x+1=x^2
=>-4x+1=0 và x>=0
=>x=1/4
b: =>x>=-1 và x^2+x+1=x^2+2x+1
=>x=0
c: =>x>=1 và 4x^2-8x+1=x^2-2x+1
=>x>=1 và 3x^2-6x=0
=>x=2
b: =>x>=-1 và 5x^2-2x+2=x^2+2x+1
=>x>=-1 và 4x^2-4x+1=0
=>x=1/2
b: =>căn 4x^2-x+1=2x+3
=>x>=-3/2 và 4x^2-x+1=(2x+3)^2=4x^2+12x+9
=>x>=-3/2 và -13x=8
=>x=-8/13
1) \(\sqrt{x^2+x}=x\) (Thỏa mẵn với mọi x)
\(\Leftrightarrow x^2+x=x^2\)
\(\Leftrightarrow x^2+x-x^2=0\)
\(\Leftrightarrow x=0\)
Vậy \(x=0\)
2) \(\sqrt{1-x^2}=x-1\) (ĐK: \(x\le1\) )
\(\Leftrightarrow1-x^2=\left(x-1\right)^2\)
\(\Leftrightarrow1-x^2=x^2-2x+1\)
\(\Leftrightarrow-x^2-x^2+2x=1-1\)
\(\Leftrightarrow-2x^2+2x=0\)
\(\Leftrightarrow-2x\left(x-1\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}-2x=0\\x-1=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\left(tm\right)\\x=1\left(tm\right)\end{matrix}\right.\)
Vậy: \(S=\left\{0;1\right\}\)
\(\sqrt{1-2x^2}=x-1\) (ĐK: \(x\le\sqrt{\dfrac{1}{2}}\))
\(\Leftrightarrow1-2x^2=\left(x-1\right)^2\)
\(\Leftrightarrow1-2x^2=x^2-2x+1\)
\(\Leftrightarrow-2x^2-x^2+2x=1-1\)
\(\Leftrightarrow-3x^2+2x=0\)
\(\Leftrightarrow-x\left(3x-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}-x=0\\3x-2=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\left(tm\right)\\x=\dfrac{2}{3}\left(tm\right)\end{matrix}\right.\)
Vậy: \(S=\left\{0;\dfrac{2}{3}\right\}\)
\(\sqrt{x^2-2x}=2-x\) (ĐK: \(\left\{{}\begin{matrix}x\le0\\x\ge2\end{matrix}\right.\) )
\(\Leftrightarrow x^2-2x=\left(2-x\right)^2\)
\(\Leftrightarrow x^2-2x=4-4x+x^2\)
\(\Leftrightarrow x^2-x^2-2x+4x=4\)
\(\Leftrightarrow2x=4\)
\(\Leftrightarrow x=2\left(tm\right)\)
Vậy: \(x=2\)
\(\sqrt{x^2-4}-x+2=0\) (ĐK: \(\left\{{}\begin{matrix}x\le-2\\x\ge2\end{matrix}\right.\))
\(\Leftrightarrow\sqrt{x^2-4}=x-2\)
\(\Leftrightarrow x^2-4=\left(x-2\right)^2\)
\(\Leftrightarrow x^2-4=x^2-4x+4\)
\(\Leftrightarrow x^2-x^2+4x=4+4\)
\(\Leftrightarrow4x=8\)
\(\Leftrightarrow x=2\left(tm\right)\)
Vậy: \(x=2\)