1.
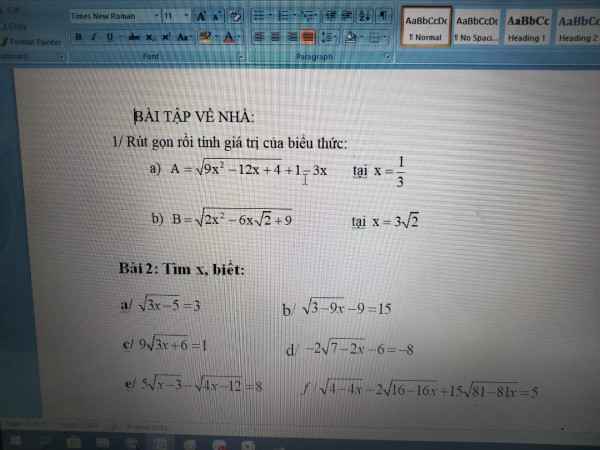
\(A=\sqrt{\left(3x-2\right)^2}+1-3x=\left|3x-2\right|+1-3x\)
\(=\left[{}\begin{matrix}-1\left(\text{với x}\ge\dfrac{2}{3}\right)\\3-6x\left(\text{với x}< \dfrac{2}{3}\right)\end{matrix}\right.\)
Do \(x=\dfrac{1}{3}< \dfrac{2}{3}\Rightarrow A=3-6x=1\)
b.
\(B=\sqrt{\left(\sqrt{2}x-3\right)^2}=\left|2\sqrt{x}-3\right|\)
\(=\left[{}\begin{matrix}\sqrt{2}x-3\left(\text{với x}\ge\dfrac{3\sqrt{2}}{2}\right)\\3-\sqrt{2}x\left(\text{với x}< \dfrac{3\sqrt{2}}{2}\right)\end{matrix}\right.\)
Tại \(x=3\sqrt{2}>\dfrac{3\sqrt{2}}{2}\Rightarrow B=\sqrt{2}x-3=\sqrt{2}.3\sqrt{2}-3=3\)
Đúng 0
Bình luận (0)
