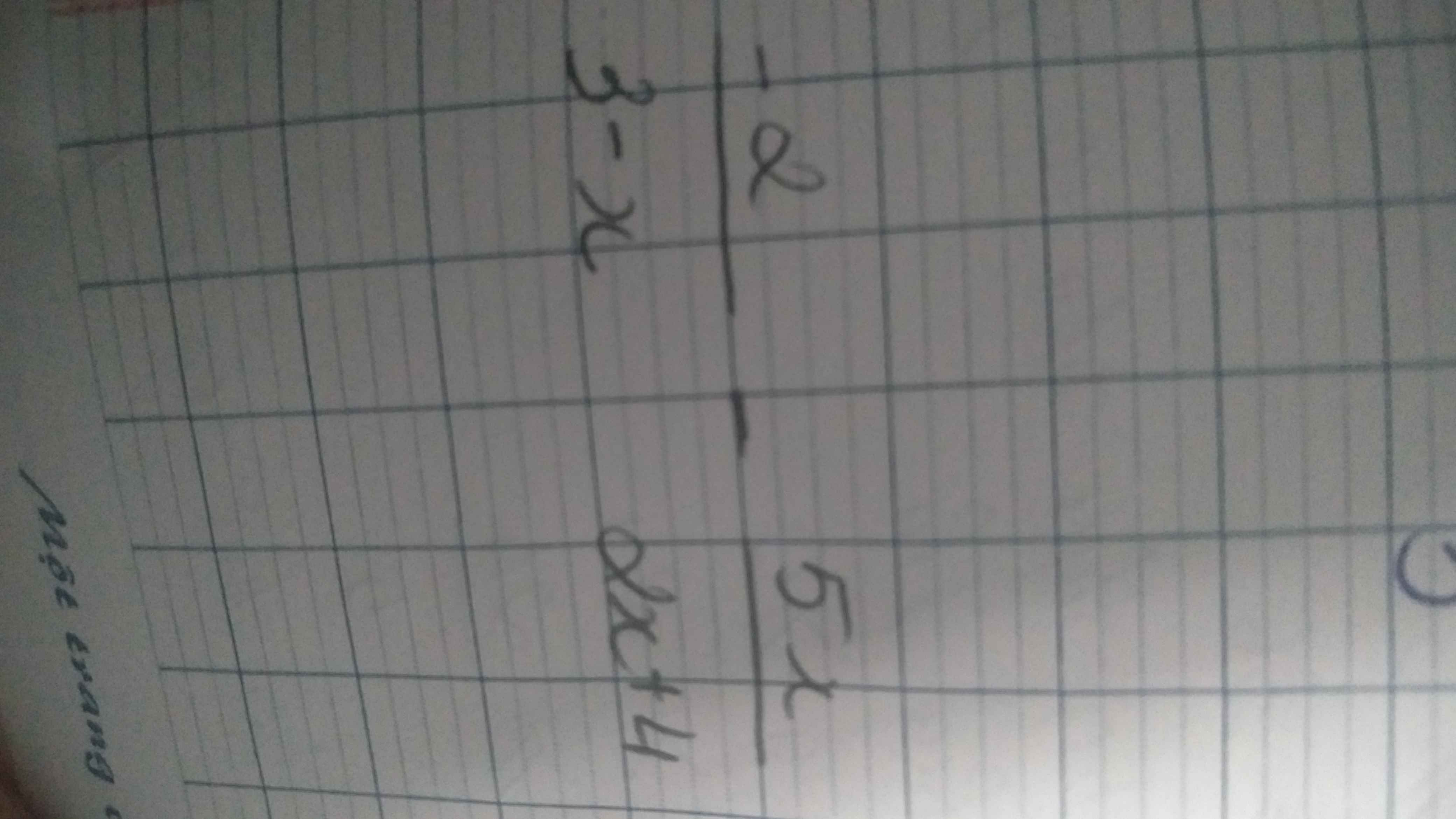\(a,\sqrt{\sqrt{5}-\sqrt{3-\sqrt{29-12\sqrt{5}}}}\\ =\sqrt{\sqrt{5}-\sqrt{3-\left(2\sqrt{5}-3\right)}}\\ =\sqrt{\sqrt{5}-\sqrt{6-2\sqrt{5}}}\\ =\sqrt{\sqrt{5}-\left(\sqrt{5}-1\right)}\\ =\sqrt{1}=1\)
\(b,\sqrt{13+30\sqrt{2+\sqrt{9+4\sqrt{2}}}}\\ =\sqrt{13+30\sqrt{2+\left(2\sqrt{2}+1\right)}}\\ =\sqrt{13+30\sqrt{3+2\sqrt{2}}}\\ =\sqrt{13+30\left(\sqrt{2}+1\right)}\\ =\sqrt{43+30\sqrt{2}}\\ =5+3\sqrt{2}\)
\(c,\sqrt{1+\sqrt{3+\sqrt{13+4\sqrt{3}}}}+\sqrt{1-\sqrt{3-\sqrt{13-4\sqrt{3}}}}\\ =\sqrt{1+\sqrt{3+\left(2\sqrt{3}+1\right)}}+\sqrt{1-\sqrt{3-\left(2\sqrt{3}-1\right)}}\\ =\sqrt{1+\sqrt{4+2\sqrt{3}}}+\sqrt{1-\sqrt{4-2\sqrt{3}}}\\ =\sqrt{1+\left(\sqrt{3}+1\right)}+\sqrt{1-\left(\sqrt{3}-1\right)}\\ =\sqrt{2+\sqrt{3}}+\sqrt{2-\sqrt{3}}\)
Đặt \(A=\sqrt{2+\sqrt{3}}+\sqrt{2-\sqrt{3}}\)
\(A^2=4+2\sqrt{\left(2+\sqrt{3}\right)\left(2-\sqrt{3}\right)}=4+2=6\\ A=\sqrt{6}\)
Vậy gt biểu thức là \(\sqrt{6}\)
\(d,\sqrt{5-\sqrt{13+4\sqrt{3}}}+\sqrt{3+\sqrt{13+4\sqrt{3}}}\\ =\sqrt{5-\left(2\sqrt{3}+1\right)}+\sqrt{3+\left(2\sqrt{3}+1\right)}\\ =\sqrt{4-2\sqrt{3}}+\sqrt{4+2\sqrt{3}}\\ =\sqrt{3}-1+\sqrt{3}+1=2\sqrt{3}\)
\(4,\)
\(A=\sqrt{2-\sqrt{3}}+\sqrt{2+\sqrt{3}}\\ A^2=2-\sqrt{3}+2+\sqrt{3}+2\sqrt{\left(2-\sqrt{3}\right)\left(2+\sqrt{3}\right)}\\ A^2=4+2=6\\ A=\sqrt{6}\\ B=\sqrt{4-\sqrt{7}}-\sqrt{4+\sqrt{7}}\\ B^2=4-\sqrt{7}+4+\sqrt{7}-2\sqrt{\left(4-\sqrt{7}\right)\left(4+\sqrt{7}\right)}\\ B^2=8-2\sqrt{9}=8-6=2\\ B=\sqrt{2}\)
\(5,\\ a,\sqrt{5+2\sqrt{6}}-\sqrt{5-2\sqrt{6}}\\ =\sqrt{\left(\sqrt{2}+\sqrt{3}\right)^2}-\sqrt{\left(\sqrt{3}-\sqrt{2}\right)^2}\\ =\sqrt{2}+\sqrt{3}-\sqrt{3}+\sqrt{2}=2\sqrt{2}\\ b,\sqrt{7-2\sqrt{10}}-\sqrt{7+2\sqrt{10}}\\ =\left(\sqrt{5}-\sqrt{2}\right)-\left(\sqrt{2}+\sqrt{5}\right)=-2\sqrt{2}\\ c,\sqrt{24+8\sqrt{5}}+\sqrt{9-4\sqrt{5}}\\ =\left(2\sqrt{5}-2\right)+\left(\sqrt{5}-2\right)\\ =3\sqrt{5}\\ d,\sqrt{17-12\sqrt{2}}+\sqrt{9+4\sqrt{2}}\\ =\left(3-2\sqrt{2}\right)+\left(2\sqrt{2}+1\right)\\ =4\)






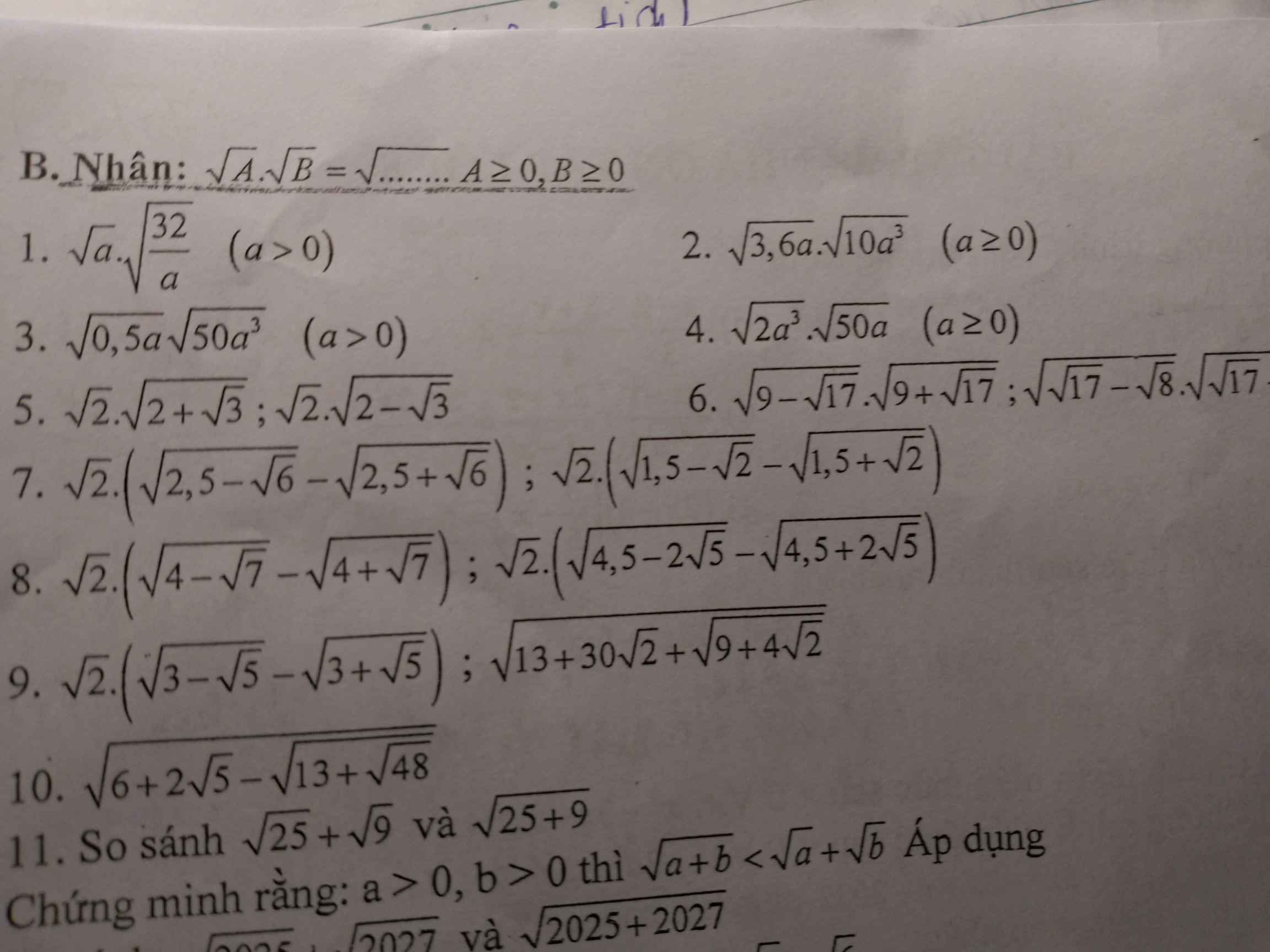

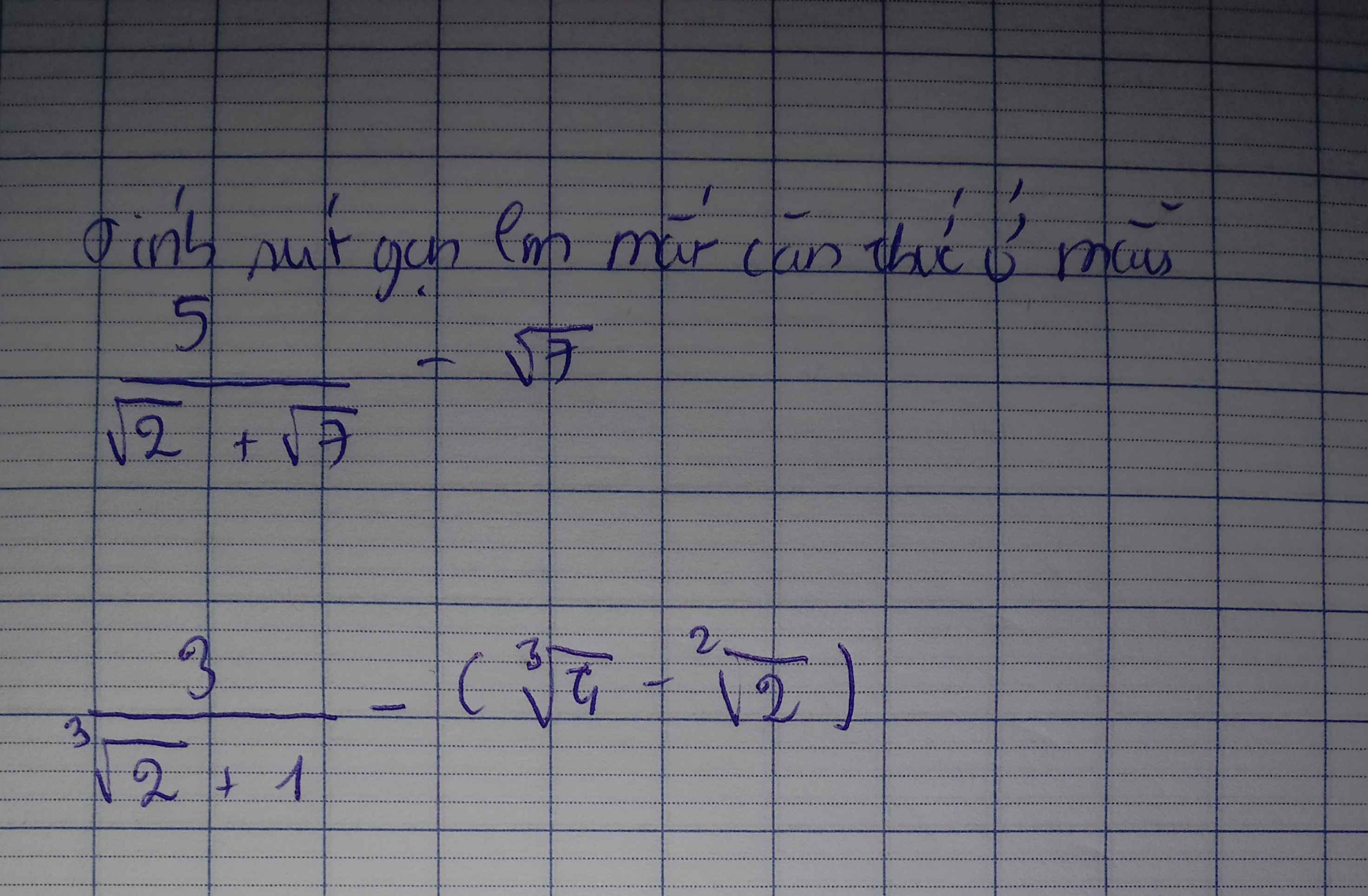

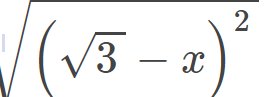
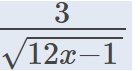 GIÚP MÌNH VỚI Ạ MÌNH CẦN GẤP Ạ
GIÚP MÌNH VỚI Ạ MÌNH CẦN GẤP Ạ