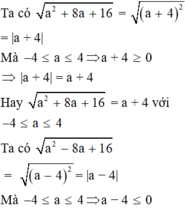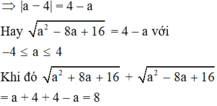\(a^4+16\ge2a^3+8a\)

Những câu hỏi liên quan
a^4+16>=2a^3+8a
Ta có : \((a^4+16)− ( 2 a ^3 + 8 a )\)
\(a ^4 + 16 − 2 a ^3 − 8 a\)
\(a ^4 + 16 − 2 ^3 − 8 a + 8 a ^2 − 8 a ^2\)
\((a^4-8a^2+16)-(2^3-8a^2+8a)\)
\(\left(a^2-4\right)^2-2a\left(a-2\right)^2\)
\(\left(a+2\right)^2\left(a-2\right)^2-2a\left(a-2\right)^2\)
\(\left(a-2\right)^2\left[\left(a+2\right)^2-2a\right]^{ }\)
\(( a − 2 ) 2 ( a ^2 + 4 a + 4 − 2 a )\)
\(( a − 2 ) ^2 ( a ^2 + 2 a + 4 )\)
\(( a − 2 ) ^2 [ ( a ^2 + 2 a + 1 ) + 3 ]\)
\(( a − 2 ) ^2 [ ( a + 2 ) ^2 + 3 ]\)
\(Vì\) \( ( a − ^2 ) 2 [ ( a + 2 ) ^2 + 3 ] ≥ 0\)
\( ( a ^4 + 16 ) − ( 2 a ^3 + 8 a ) ≥ 0\)
\(a ^4 + 16 ≥ 2 a ^3 + 8 a ( đ p c m )\)
Đúng 2
Bình luận (1)
Rút gọn biểu thức
a
2
+
8
a
+
16
+
a
2
-
8
a
+
16
với
-...
Đọc tiếp
Rút gọn biểu thức a 2 + 8 a + 16 + a 2 - 8 a + 16 với - 4 ≤ a ≤ 4 ta được
A. 2a
B. 8
C. -8
D. -2a
Chứng tỏ: a^4+16>=2a^3 + 8a với mọi a
chứng minh bất đẳng thức 2a^3+8a<=a^4+16
\(2a^3+8a\le a^4+16\)
\(\Leftrightarrow2a^3+8a-a^4-16\le0\)
\(\Leftrightarrow\left(2a^3-a^4\right)+\left(8a-16\right)\le0\)
\(\Leftrightarrow-a^3\left(a-2\right)+8\left(a-2\right)\le0\)
\(\Leftrightarrow-\left(a-2\right)\left(a^3-8\right)\le0\Leftrightarrow-\left(a-2\right)^2\left(a^2+2a+4\right)\le0\)
TA THẤY : \(\left(a-2\right)^2\left(a^2+2a+4\right)\ge0\)\(\Leftrightarrow-\left(a-2\right)^2\left(a^2+2a+4\right)\le0\)\(\Leftrightarrow2a^3+8a\le a^4+16\left(dpcm\right)\)
DẤU " = " XẢY RA KHI X = 2
TK CHO MK NKA !!!
Đúng 0
Bình luận (0)
CM: a4+16>=2a3+8a
Gỉa sử \(a^4+16\ge2a^3+8a\Leftrightarrow a^4-2a^3-8a+16\ge0\)
\(\Leftrightarrow a^3\left(a-2\right)-8\left(a-2\right)\ge0\Leftrightarrow\left(a-2\right)\left(a^3-8\right)\ge0\)
\(\Leftrightarrow\left(a-2\right)\left(a-2\right)\left(a^2+2a+4\right)\ge0\Leftrightarrow\left(a-2\right)^2\left(a^2+2a+4\right)\ge0\)
Ta thấy \(\left(a-2\right)^2\left(a^2+2a+4\right)\ge0\forall a\)nên giả sử là đúng
Vậy \(a^4+16\ge2a^3+8a\)
Đúng 0
Bình luận (0)
rút gọn : A = a4 -16 / a4 - 4a3 + 8a2 -16a +16
A = (a^2+4).(a^2-4)/(a^4+4a^2)-(4a^3+16a)+(4a^2+16)
= (a^2+4).(a^2-4)/(a^2+4).(a^2-4a+4)
= (a^2+4).(a-2).(a+2)/(a^2+4).(a-2)^2
= a+2/a-2
Tk mk nha
Đúng 0
Bình luận (0)
Chứng minh
a.2a^3 + 8a < hoặc = a^4 +16
b. x^2+16>= 2x^2+8x
a)\(2a^3+8a\le a^4+16\)
\(\Leftrightarrow a^4-2a^3-8a+16\ge0\)
\(\Leftrightarrow a^3\left(a-2\right)-8\left(a-2\right)\ge0\)
\(\Leftrightarrow\left(a-2\right)\left(a^3-8\right)\ge0\)
\(\Leftrightarrow\left(a-2\right)\left(a-2\right)\left(a^2+2a+4\right)\ge0\)
\(\Leftrightarrow\left(a-2\right)^2\left(a^2+2a+4\right)\ge0\)(luôn đúng)
=>đpcm
Đúng 0
Bình luận (5)
a.
2a3 + 8a \(\le\) a4 +16
<=>2a3 + 8a - a4 -16 \(\le\) 0
<=> a4 - 2a3 -8a + 16 \(\ge\) 0
<=> a3(a - 2) - 8(a - 2) \(\ge\) 0
<=> (a - 2)(a3 - 8)\(\ge\) 0
<=> (a - 2)(a - 2)(a2 + 2a + 4) \(\ge\) 0
<=> (a - 2)2 [(a + 1)2 +3] \(\ge\) 0
Ta thấy (a - 2)2 \(\ge\) 0 \(\forall\)x và (a + 1)2 \(\ge\) 0 \(\forall\)x nên bất đẳng thức cần c/m đúng
b. đề sao sao á :))
Đúng 0
Bình luận (0)
chứng minh rằng 2a^3+8a<=a^4+16
Ta có:a4+16-2a3-8a
=(a4-8a2+16)-(2a3-8a2+8a)
=(a2-4)2-2a(a-2)2
=(a-2)2[(a+2)2-2a]
=(a-2)2(a2+4a+4-2a)
=(a-2)2(a2+2a+4)
=(a-2)2[(a+1)2+3]\(\)\(\ge\)0 với mọi a
=>a4+16-2a3-8a \(\ge\)0
<=>a4+16\(\ge\)2a3+8a
Đúng 1
Bình luận (1)
Cho phân thức: \(M=\frac{a^4-16}{a^4-4a^3+8a^2-16a+16}\)
Tìm giá trị nguyên của a để M nhận giá trị nguyên.
\(M=\frac{a^4-16}{a^4-4a^3+8a^2-16a+16}=\frac{\left(a^2-4\right)\left(a^2+4\right)}{a^4-4a^3+4a^2+4a^2-16a+16}=\frac{\left(a-2\right)\left(a+2\right)\left(a^2+4\right)}{a^2\left(a^2-4a+4\right)+4\left(a^2-4a+4\right)}\)
\(=\frac{\left(a-2\right)\left(a+2\right)\left(a^2+4\right)}{\left(a^2+4\right)\left(a-2\right)^2}=\frac{a+2}{a-2}=\frac{a-2+4}{a-2}=1+\frac{4}{a-2}\)
Để \(M\in Z\Leftrightarrow a-2\inƯ\left(4\right)=\left\{\pm1;\pm2;\pm4\right\}\)
Ta có bảng:
| a - 2 | 1 | -1 | 2 | -2 | 4 | -4 |
| a | 3 | 1 | 4 | 0 | 6 | -2 |
Vậy...
Đúng 0
Bình luận (0)
Cho M=\(\frac{a^4-16}{a^4-4a^3+8a^2-16a+16}\)
Tìm các gt nguyên của A để M thuộc Z