Cho tứ giác ABCD
AB//CD, Góc C = 65 độ, góc D = 95 độ, tính góc A và góc B
Những câu hỏi liên quan
Bài 3: Cho tứ giác ABCD có AB//CD và góc D =60 độ
a) Tính số đo góc A?
b) Biết góc B phần góc D = 4/5. Tính góc B, góc C
Bài 4: Cho tứ giác ABCD, góc A - góc B = 40 độ. Các tia phân giác của góc C, góc D cắt nhau tại O. Cho biết góc COD= 110 độ. Chứng minh rằng AB vuông góc với BC
Nhờ các bạn hướng dẫn mình hai bài này
a) Vì AB//CD, ta có góc ACD = góc BCD = 180 - góc D = 180 - 60 = 120 độ.
Vì AB//CD, ta có góc ACD = góc BAD.
Vậy số đo góc A là 120 độ.
b) Gọi góc BCD là x độ.
Theo giả thiết, góc B phần góc D = 4/5, ta có:
góc B = (4/5) * góc D
= (4/5) * 60
= 48 độ.
Vì AB//CD, ta có góc BCD = góc BAD.
Vậy góc BAD = góc BCD = x độ.
Vì tứ giác ABCD là tứ giác lồi, tổng các góc trong tứ giác ABCD là 360 độ.
Ta có: góc A + góc B + góc C + góc D = 360 độ.
Vì góc D = 60 độ, góc A = 120 độ và góc B = 48 độ, ta có:
120 + 48 + góc C + 60 = 360
góc C = 360 - 120 - 48 - 60 = 132 độ.
Vậy số đo góc B là 48 độ và số đo góc C là 132 độ.
* Ib = bài 4
Đúng 0
Bình luận (0)
Cho tứ giác ABCD có AB = AD, góc B = 90 độ, góc A = 60 độ, góc D = 135 độ. a) Tính góc C và chứng minh BD = BC. b) Kẻ AE vuông góc với CD. Tính các góc của tam giác AEC
Cho tứ giác ABCD có AB = AD, góc B = 90 độ, góc A = 60 độ, góc D = 135 độ. a) Tính góc C và chứng minh BD = BC. b) Kẻ AE vuông góc với CD. Tính các góc của tam giác AEC
Cho tứ giác ABCD có góc A = 65 độ, góc B = 117 độ, góc C = 71 độ. Tính số đo của góc D =?
a 126 độ
b 63 độ
c 119 độ
d 107 độ
Xem thêm câu trả lời
1. cho tứ giác ABCD biết góc A : góc B : góc c ; góc D 1:2:3:4 tính các góc của tứ giác2. chó tứ giác ABCD có góc A 105 độ: góc B 130 độ, góc C-góc D 25 độ. Tính góc C, góc D3. Cho tứ giác ABCD có góc A 57 độ, C 110 độ, D 75 độ. Tính góc ngoài tại B4. Chứng minh rằng: Biết 1 tứ giác tổng 2 đường chéo lớn hơn nửa chu vi của tứ giác 5. Cho tứ giác ABCD có góc B+gócD 180 độ, AC là tia phân giác góc A. Chứng minh cạnh CB cạnh CD
Đọc tiếp
1. cho tứ giác ABCD biết góc A : góc B : góc c ; góc D = 1:2:3:4 tính các góc của tứ giác
2. chó tứ giác ABCD có góc A =105 độ: góc B = 130 độ, góc C-góc D = 25 độ. Tính góc C, góc D
3. Cho tứ giác ABCD có góc A = 57 độ, C= 110 độ, D= 75 độ. Tính góc ngoài tại B
4. Chứng minh rằng: Biết 1 tứ giác tổng 2 đường chéo lớn hơn nửa chu vi của tứ giác
5. Cho tứ giác ABCD có góc B+gócD= 180 độ, AC là tia phân giác góc A. Chứng minh cạnh CB = cạnh CD
1: Đặt góc A=a; góc B=b; góc C=c; góc D=d
Theo đề, ta có: a/1=b/2=c/3=d/4 và a+b+c+d=360
Áp dụng tính chất của DTSBN, ta được:
a/1=b/2=c/3=d/4=(a+b+c+d)/(1+2+3+4)=360/10=36
=>a=36; b=72; c=108; d=144
2:
góc C+góc D=360-130-105=230-105=125
góc C-góc D=25 độ
=>góc C=(125+25)/2=75 độ và góc D=75-25=50 độ
3:
góc B=360-57-110-75=118 độ
số đo góc ngoài tại B là:
180-118=62 độ
Đúng 0
Bình luận (0)
Cho tứ giác ABCD có góc ngoài tại điểm A =65 độ, góc ngoài tại điểm B=100 độ, góc ngoài ở điểm C= 60 độ . Tính góc ngoài ở điểm D
Ta có tổng các góc trong tứ giác là:
\(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^o\)
Mà các góc ngoài của các đỉnh của được tính tương tự:
Tổng các góc ngoài của các đỉnh là:
\(\widehat{A_{\text{ngoài}}}+\widehat{B_{\text{ngoài}}}+\widehat{C_{\text{ngoài}}}+\widehat{D_{\text{ngoài}}}=360^o\)
\(\Rightarrow\widehat{D_{\text{ngoài}}}=360^o-\left(65+100+60\right)=135^o\)
Đúng 1
Bình luận (0)
Số đo góc ngoài tại điểm D là:
360-65-100-60=135 độ
Đúng 1
Bình luận (0)
Cho tứ giác ABCD , AB song song CD góc A = góc 3D , góc B – góc C = 30 độ
Tính góc A , B , C , D
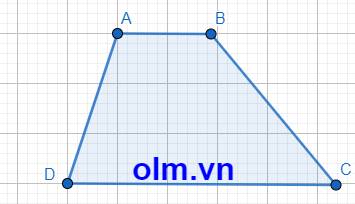
Vì AB//CD nên Góc A và góc D là hai góc trong cùng phía
\(\widehat{A}\)+ \(\widehat{D}\) = 1800 ⇒ \(\widehat{D}\) + 3\(\widehat{D}\) = 1800 ⇒ \(\widehat{D}\) = 1800:4 = 450
\(\widehat{A}\) = 450.3 =1350
\(\widehat{B}\)+\(\widehat{C}\) = 1800 ⇒ \(\widehat{B}\) + \(\widehat{B}\) - 300 = 1800 ⇒2\(\widehat{B}\) =2100 ⇒ \(\widehat{B}\) = 1050
\(\widehat{C}\) = 1050 - 300 = 750
Đúng 0
Bình luận (0)
Cho tứ giác ABCD có AB=BC: CD=DA
a) Chứng minh BD là đường trung trức của AC
B) Cho góc B = 100 độ, góc D = 80 độ. Tính góc A và góc C
a: BA=BC
DC=DA
=>BD là trung trực của AC
b: Xét ΔABD và ΔCBD có
BA=BC
BD chung
DA=DC
=>ΔABD=ΔCBD
=>góc BAD=góc BCD=(360-100-80)/2=90 độ
Đúng 0
Bình luận (0)
cho tứ giác abcd có goc b=100 độ góc d bằng 80 độ, cb=cd
a, nếu góc a- góc c =40 độ hãy tính các góc còn lại của tứ giác
b chứng minh góc bac=góc dac