Tìm min hoặc max của bthc sau: 2x2-4xy+4y2+2x+5
Những câu hỏi liên quan
Tìm max hoặc min của A= -2x^2-8x+1
B=3x^2+3x-1
C=7x-2x^2+3
D=-4xy+4x-y^2-5x^2+3
\(B=3x^2+3x-1\)
\(=3\left(x^2+x-\dfrac{1}{3}\right)\)
\(=3\left(x^2+x+\dfrac{1}{4}-\dfrac{7}{12}\right)\)
\(=3\left(x+\dfrac{1}{2}\right)^2-\dfrac{7}{4}>=-\dfrac{7}{4}\forall x\)
Dấu '=' xảy ra khi x+1/2=0
=>\(x=-\dfrac{1}{2}\)
\(C=-2x^2+7x+3\)
\(=-2\left(x^2-\dfrac{7}{2}x-\dfrac{3}{2}\right)\)
\(=-2\left(x^2-2\cdot x\cdot\dfrac{7}{4}+\dfrac{49}{16}-\dfrac{73}{16}\right)\)
\(=-2\left(x-\dfrac{7}{4}\right)^2+\dfrac{73}{8}< =\dfrac{73}{8}\forall x\)
Dấu '=' xảy ra khi x-7/4=0
=>x=7/4
Đúng 0
Bình luận (0)
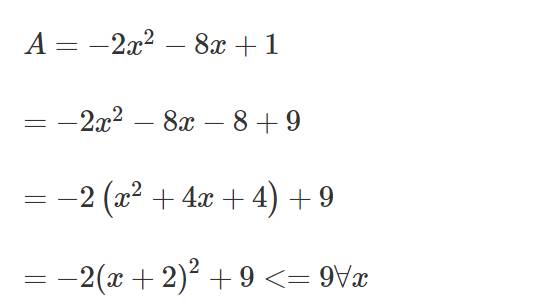
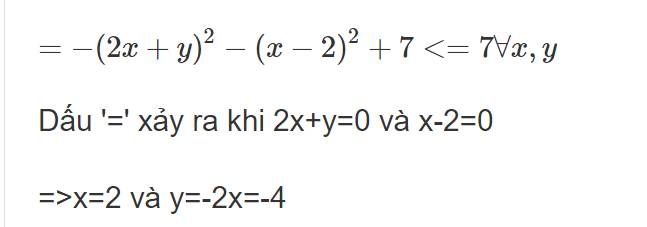
Giải giúp mk bài toán~
Tìm min hoặc max của biểu thức sau
x2+5y2+2x-4xy-10y+14
Cảm ơn nha!
(ai có nhu cầu kb vs mk ko)
Đầu bài bạn thiếu đúng ko xem lại ik
Đúng 0
Bình luận (0)
Tìm GTLN hoặc GTNN của các đa thưc sau:
Xem chi tiết
a, -x2 + 2x + 3
b, x2 - 2x + 4y2 - 4y + 8 c, -x2 - y2 + xy + 2x + 2y + 4 d, x2 + 5y2 - 4xy - 2y + 2015 e, 2x2 + y2 + 6x + 2y + 2xy + 2018
A= -x2+2x+3
=>A= -(x2-2x+3)
=>A= -(x2-2.x.1+1+3-1)
=>A=-[(x-1)2+2]
=>A= -(x+1)2-2
Vì -(x+1)2 ≤0=> A≤-2
Dấu "=" xảy ra khi
-(x+1)2=0 => x=-1
Vây A lớn nhất= -2 khi x= -1
Đúng 4
Bình luận (0)
B=x2-2x+4y2-4y+8
=> B= (x2-2x+1)+(4y2-4y+1)+6
=> B=(x-1)2+(2y+1)2+6
=> B lớn nhất=6 khi x=1 và y=-1/2
Đúng 2
Bình luận (0)
Tìm Min hoặc Max của
C = 2x^2 + y^2 - 2xy - 2y + 5
\(C=2x^2+y^2-2xy-2y+5\)
\(\Rightarrow2C=4x^2+2y^2-4xy-4y-10\)
\(2C=\left(2x\right)^2-2.2x.y+y^2+y^2-4y+4-14\)
\(2C=\left(2x-y\right)^2+\left(y-2\right)^2-14\)
Với mọi x, y ta có: \(\left(2x-y\right)^2\ge0;\left(y-2\right)^2\ge0\)
\(\Rightarrow\left(2x-y\right)^2+\left(y-2\right)^2\ge0\)
\(\Rightarrow2C=\left(2x-y\right)^2+\left(y-2\right)^2-14\ge-14\)
\(\Rightarrow C\ge\frac{-14}{2}=-7\)
Dấu bằng xảy ra khi: \(\hept{\begin{cases}2x-y=0\\y-2=0\end{cases}\Leftrightarrow\hept{\begin{cases}2x=y\\y=2\end{cases}\Leftrightarrow}\hept{\begin{cases}2x=2\\y=2\end{cases}}\Leftrightarrow\hept{\begin{cases}x=1\\y=2\end{cases}}}\)
Vậy x=1 ; y=2 thì min C = -7
HỌC TỐT <3
Đúng 0
Bình luận (0)
tìm min hoặc max của 2x2+x
Tìm GTNN của biểu thức:
2x2 + 4y2 - 4xy - 4y - 2x + 2
\(A=\left(x^2+4y^2+1-4xy+2x-4y\right)+\left(x^2-4x+4\right)-3\)
\(A=\left(x-2y+1\right)^2+\left(x-2\right)^2-3\ge-3\)
Dấu "=" xảy ra khi \(\left(x;y\right)=\left(2;\dfrac{3}{2}\right)\)
Đúng 0
Bình luận (0)
tìm min hoặc max của 2x2 +x
Bài này tìm được min thôi
Ta có: \(2x^2+x=2\left(x^2+\frac{1}{2}x+\frac{1}{16}\right)-\frac{1}{8}=2\left(x+\frac{1}{4}\right)^2-\frac{1}{8}\ge-\frac{1}{8}\left(\forall x\right)\)
Dấu "=" xảy ra khi: \(2\left(x+\frac{1}{4}\right)^2=0\Rightarrow x=-\frac{1}{4}\)
Vậy Min = -1/8 khi x = -1/4
1. Tìm max hoặc min:
a. A = x^2 - 5x - 1
b. B = 1/4x - x + 5.
c. C = x^2 - 4xy + 7y^2 - 2y +3
d. D = 5x^2 - xy + 1/24y^2 + 2x - 1
e. E = x^2 - 3xy + y - 2y - 1
2. Tìm x:
a. ( 2x - 3 )^2 - ( 4x + 1 ).( 4x - 1 ) = ( 2x - 1 ).( 3 - 7x )
b. 1/16x^2 - ( 3x + 5 ) = 0
c. 4.( x - 3 ) - ( x + 2 ) = 0
tìm min, max của các biểu thức sau
a, √ x2-2x+5
b, 2 + √x2-4x+5
Không có max
`a)sqrt{x^2-2x+5}`
`=sqrt{x^2-2x+1+4}`
`=sqrt{(x-1)^2+4}`
Vì `(x-1)^2>=0`
`=>(x-1)^2+4>=4`
`=>sqrt{(x-1)^2+4}>=sqrt4=2`
Dấu "=" xảy ra khi `x=1.`
`b)2+sqrt{x^2-4x+5}`
`=2+sqrt{x^2-4x+4+1}`
`=2+sqrt{(x-2)^2+1}`
Vì `(x-2)^2>=0`
`=>(x-2)^2+1>=1`
`=>sqrt{(x-2)^2+1}>=1`
`=>sqrt{(x-2)^2+1}+2>=3`
Dấu "=" xảy ra khi `x=2`
Đúng 3
Bình luận (2)