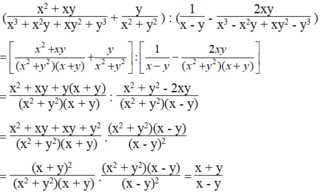x2y+xy2-x-y

Những câu hỏi liên quan
x
2
+
x
y
x
3
+
x
2
y
+
x
y
2
+
y
3...
Đọc tiếp
x 2 + x y x 3 + x 2 y + x y 2 + y 3 + y x 2 + y 2 : 1 x - y - 2 x y x 3 - x 2 y + x y 2 - y 3
E=(x3-x2y+xy2-y3)(x+y) với x=2, y=1/2
Ta có: \(\left(x^3-x^2y+xy^2-y^3\right)\left(x+y\right)\)
\(=\left[x^2\left(x-y\right)+y^2\left(x-y\right)\right]\left(x+y\right)\)
\(=\left(x^2-y^2\right)\left(x^2+y^2\right)\)
\(=x^4-y^4=2^4-\left(\dfrac{1}{2}\right)^4=16-\dfrac{1}{16}=\dfrac{255}{16}\)
Đúng 1
Bình luận (0)
Hệ phương trình
x
2
y
+
x
y
2
6
x
y
+
x
+
y...
Đọc tiếp
Hệ phương trình x 2 y + x y 2 = 6 x y + x + y = 5
A. Có 2 nghiệm (5; 1) và (1; 5)
B. Có 2 nghiệm (2; 1) và (1; 2)
C. Có 1 nghiệm là (2; 2)
D. Có 4 nghiệm (1; 2); (2; 1); (1; 5) và (5; 1)
Chứng minh rằng:
x3 + y3 ≥ x2y + xy2, ∀x, y ≥ 0
Với x ≥ 0; y ≥ 0 thì x + y ≥ 0
Ta có: x3 + y3 ≥ x2y + xy2
⇔ (x3 + y3) – (x2y + xy2) ≥ 0
⇔ (x + y)(x2 – xy + y2) – xy(x + y) ≥ 0
⇔ (x + y)(x2 – xy + y2 – xy) ≥ 0
⇔ (x + y)(x2 – 2xy + y2) ≥ 0
⇔ (x + y)(x – y)2 ≥ 0 (Luôn đúng vì x + y ≥ 0 ; (x – y)2 ≥ 0)
Dấu « = » xảy ra khi (x – y)2 = 0 ⇔ x = y.
Đúng 0
Bình luận (0)
Chứng minh:
(x3+x2y+xy2+y3)(x-y)=x3-y3
(x3+x2y+xy2+y3)(x-y)
=x(x3+x2y+xy2+y3)-y(x3+x2y+xy2+y3)
=x4+x3y+x2y2+xy3-x3y-x2y2+xy3+y4
= x4+y4
đề sai bạn xem lại đề
Đúng 0
Bình luận (1)
Tính giá trị của các biểu thức: x3 + x2y + xy2 + 2xy(x + y)
biết x + y = 2
Đề sai r bn, nếu x,y thay đổi thì tổng biểu thức cũng thay đổi
Đúng 0
Bình luận (0)
Giá trị của biểu thức D
x
3
–
x
2
y
–
x
y
2
+
y
3
khi x y là A. 3 B. 2 C. 1 D. 0
Đọc tiếp
Giá trị của biểu thức D = x 3 – x 2 y – x y 2 + y 3 khi x = y là
A. 3
B. 2
C. 1
D. 0
D = ( x 3 + y 3 ) – x y ( x + y ) = ( x + y ) ( x 2 – x y + y 2 ) – x y ( x + y ) = ( x + y ) ( x 2 – x y + y 2 – x y ) = ( x + y ) [ x ( x – y ) – y ( x – y ) ] = ( x + y ) ( x – y ) 2
Vì x = y ó x – y = 0 nên D = ( x + y ) ( x – y ) 2 = 0
Đáp án cần chọn là: D
Đúng 0
Bình luận (0)
Giá trị của biểu thức B
x
3
+
x
2
y
–
x
y
2
–
y
3
tại x 3,25 ; y 6,75 là A. 350 B. -350 C. 35 D. -35
Đọc tiếp
Giá trị của biểu thức B = x 3 + x 2 y – x y 2 – y 3 tại x = 3,25 ; y = 6,75 là
A. 350
B. -350
C. 35
D. -35
Ta có
B = x 3 + x 2 y – x y 2 – y 3 = x 2 ( x + y ) – y 2 ( x + y ) = ( x 2 – y 2 ) ( x + y ) = ( x – y ) ( x + y ) ( x + y ) = ( x – y ) ( x + y ) 2
Thay x = 3,25 ; y = 6,57 ta được
B = ( 3 , 25 – 6 , 75 ) ( 3 , 25 + 6 , 75 ) 2 = - 3 , 5 . 10 2 = - 350
Đáp án cần chọn là: B
Đúng 0
Bình luận (0)
Thực hiện phép tính:
a)(x-y).(x3+x2y+xy2+y3)
b)x.(3x-18)-3.(x-4).(x-2)+8
a)\(\left(x-y\right)\left(x^3+x^2y+xy^2+y^3\right)=x^4+x^3y+x^2y^2+xy^3-x^3y-x^2y^2-xy^3-y^4=x^4-y^4\)
b) \(x\left(3x-18\right)-3\left(x-4\right)\left(x-2\right)+8=3x^2-18x-3x^2+18x-24+8=-16\)
Đúng 2
Bình luận (0)
cho ∛x + ∛y = 6
Tìm tất cả các giá trị của x và y để 2 ( x+y) = 3(∛x2y + ∛xy2)