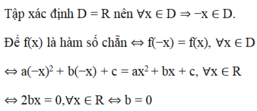Tìm điều kiện của tham số m để hàm số f(x) xác định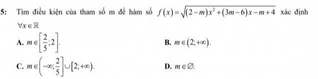

Những câu hỏi liên quan
cho hàm số y=f(x)=1/2x-2 tìm điều kiện của x để hàm số y =f(x) xác định
Tìm điều kiện của tham số m để hàm số \(y=\sqrt{2m-3sinx}\) có tập xác định là R
ĐKXĐ: 2m-3sinx>=0
=>3sin x<=2m
=>sin x<=2m/3
mà -1<=sin x<=1
nên -1<=2m/3<=1
=>-3<=2m<=3
=>-3/2<=m<=3/2
Đúng 0
Bình luận (0)
Tìm điều kiện của tham số m để hàm số sau có tập xác định là R
\(y=\dfrac{1}{\sqrt{2sin3x+2cos3x-m}}\)
Hàm xác định trên R khi với mọi x ta có:
\(2sin3x+2cos3x-m>0\)
\(\Leftrightarrow sin3x+cos3x>\dfrac{m}{2}\)
\(\Leftrightarrow\sqrt{2}sin\left(3x+\dfrac{\pi}{4}\right)>\dfrac{m}{2}\)
\(\Rightarrow\dfrac{m}{2\sqrt{2}}< \min\limits_Rsin\left(3x+\dfrac{\pi}{4}\right)=-1\)
\(\Rightarrow m< -2\sqrt{2}\)
Đúng 1
Bình luận (0)
Tìm điều kiện của tham số m để hàm số f(x) = a x 2 + bx + c là hàm số chẵn
A. a tùy ý, b = 0, c = 0
B. a tùy ý, b = 0, c tùy ý
C. a, b, c tùy ý
D. a tùy ý, b tùy ý, c = 0
Cho hàm số y = (3 – m)x2a) Tìm điều kiện của m để hàm số trên được xác định.b) Xác định m để hàm số đồng biến với mọi x < 0.c) Xác định m để y = 0 là giá trị nhỏ nhất của hàm số tại x = 0.
a, ĐKXĐ để hàm được xác định : \(3-m\ne0\)
\(\Leftrightarrow m\ne3\)
b, - Với x < 0 để hàm số đồng biến thì : \(3-m< 0\)
\(\Leftrightarrow m>3\)
Vậy ...
c, - Để y = 0 là giá trị nhỏ nhất của hàm số tại x = 0
\(\Leftrightarrow a>0\)
\(\Leftrightarrow3-m>0\)
\(\Leftrightarrow m< 3\)
Vậy ...
Đúng 2
Bình luận (0)
a) Để hàm số \(y=\left(3-m\right)x^2\) được xác định thì \(3-m\ne0\)
hay \(m\ne3\)
b) Để hàm số \(y=\left(3-m\right)x^2\) đồng biến với mọi x<0 thì \(3-m< 0\)
\(\Leftrightarrow m>3\)
c) Để y=0 là giá trị nhỏ nhất của hàm số tại x=0 thì 3-m>0
hay m<3
Đúng 2
Bình luận (0)
Tìm điều kiện của tham số m để hàm số sau có tập xác định là R
\(y=\dfrac{sin3x}{\sqrt{sin^6x+cos^6x+msinxcosx}}\)
Hàm xác định trên R khi với mọi x ta có:
\(sin^6x+cos^6x+m.sinx.cosx>0\)
\(\Leftrightarrow1-\dfrac{3}{4}sin^22x+\dfrac{m}{2}sin2x>0\)
\(\Leftrightarrow3sin^22x-2m.sin2x-4< 0\)
Đặt \(sin2x=t\in\left[-1;1\right]\Rightarrow3t^2-2mt-4< 0\)
\(\Leftrightarrow\left\{{}\begin{matrix}3.f\left(-1\right)< 0\\3.f\left(1\right)< 0\\\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}2m-1< 0\\-2m-1< 0\end{matrix}\right.\)
\(\Rightarrow-\dfrac{1}{2}< m< \dfrac{1}{2}\)
Đúng 1
Bình luận (0)
tìm điều kiện của tham số m để f(x)=x^3+(m^2-1)x^2+3x+m+1 là hàm số lẻ
Cho hàm số y=f(x) xác định, liên tục trên R\{1} và có bảng biến thiên như sau
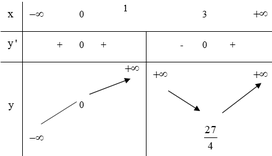
Tìm điều kiện m để phương trình f(x)=m có 3 nghiệm phân biệt
A. m< 0
B. m> 0
C. 0<m<27/4
D. m>27/4
cho hàm số y = f(x) = 5-2x
a) tìm điều kiện của x để hàm số f(x) xác định
b)tính f(-2) ; f(-1) ; f(0) ; f(1/2) ; f(4)
c)tìm x biết f(x) = -4 ; -3 ; 0 ; 5 .