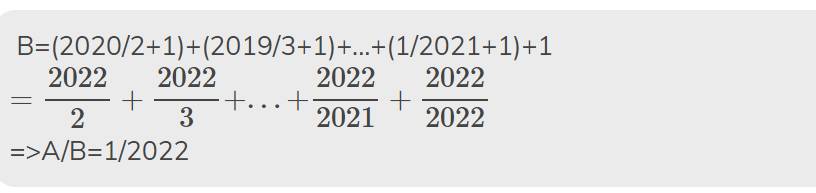-Mình làm tắt được không bạn :/?

\(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}=\dfrac{1}{2022}\)

\(\Rightarrow\dfrac{bc+ca+ab}{abc}=\dfrac{1}{a+b+c}\)

\(\Rightarrow\left(bc+ca+ab\right)\left(a+b+c\right)=abc\)

\(\Rightarrow ab\left(a+b\right)+bc\left(b+c\right)+ca\left(c+a\right)+3abc=abc\)

\(\Rightarrow ab\left(a+b\right)+bc\left(b+c\right)+ca\left(c+a\right)+2abc=0\)

\(\Rightarrow\left(a+b\right)\left(b+c\right)\left(c+a\right)=0\)

\(\Rightarrow a=-b\) hay \(b=-c\) hay \(c=-a\)

\(\Rightarrow c=2022\) hay \(a=2022\) hay \(b=2022\)

-Nếu \(a=-b\)\(\Rightarrow B=\dfrac{1}{a^{2021}}+\dfrac{1}{b^{2021}}+\dfrac{1}{c^{2021}}=\dfrac{1}{a^{2021}}-\dfrac{1}{a^{2021}}+\dfrac{1}{2022^{2021}}=\dfrac{1}{2022^{2021}}\)

-Tương tự các trường hợp còn lại.

Ta có thể viết lại M dưới dạng:

M = (1/2³) + (2/3³ - 1/2³) + (3/4³ - 2/3³) + … + (2022/2023³ - 2021/2022³)

= (1/2³) + [(2/3³ - 1/2³) + (3/4³ - 2/3³)] + … + [(2022/2023³ - 2021/2022³) + (2023/2024³ - 2022/2023³)]

= (1/2³) + (1/3³ - 1/2³) + … + (1/2023³ - 1/2022³)

= 1/2³ + (1/2³ - 1/3³) + (1/3³ - 1/4³) + … + (1/2022³ - 1/2023³)

Ta sử dụng kết quả sau đây: Với mọi số nguyên dương n, ta có

1/n³ > 1/(n+1)³

Điều này có thể được chứng minh bằng cách sử dụng đạo hàm hoặc khai triển. Do đó,

1/2³ > 1/3³
1/3³ > 1/4³
…
1/2022³ > 1/2023³

Vậy ta có

M = 1/2³ + (1/2³ - 1/3³) + (1/3³ - 1/4³) + … + (1/2022³ - 1/2023³) < 1/2³ + 1/3³ + 1/4³ + … + 1/2023³

Để chứng minh rằng M không phải là một số tự nhiên, ta sẽ chứng minh rằng tổng các số mũ ba nghịch đảo từ 1 đến 2023 không phải là một số tự nhiên. Điều này có thể được chứng minh bằng phương pháp giả sử ngược lại và dẫn đến mâu thuẫn.

Giả sử tổng các số mũ ba nghịch đảo từ 1 đến 2023 là một số tự nhiên, ký hiệu là S. Ta có:

S = 1/1³ + 1/2³ + 1/3³ + … + 1/2023³

Với mọi số nguyên dương n, ta có:

1/n³ < 1/n(n-1)

Do đó,

1/1³ < 1/(1x2)
1/2³ < 1/(2x3)
1/3³ < 1/(3x4)
...

1/2023³ < 1/(2023x2024)

Tổng các số hạng bên phải có thể được viết lại dưới dạng:

1/(1x2) + 1/(2x3) + 1/(3x4) + … + 1/(2023x2024) = (1 - 1/2) + (1/2 - 1/3) + (1/3 - 1/4) + … + (1/2023 - 1/2024) = 1 - 1/2024 < 1

Vậy tổng các số mũ ba nghịch đảo từ 1 đến 2023 cũng nhỏ hơn 1. Điều này mâu thuẫn với giả sử ban đầu rằng tổng này là một số tự nhiên. Do đó, giá trị của M không phải là một số tự nhiên.

S = 1/3 + 1/3² + 1/3³ + ... + 1/3²⁰²¹ + 1/3²⁰²²

⇒ S/3 = 1/3² + 1/3³ + 1/3⁴ + ... + 1/3²⁰²² + 1/3²⁰²³

⇒ 2S/3 = S - S/3

= (1/3 + 1/3² + 1/3³ + ... + 1/3²⁰²¹ + 1/3²⁰²²) - (1/3² +1/3³ + 1/3⁴ + ... + 1/3²⁰²² + 1/3²⁰²³)

= 1/3 - 1/3²⁰²³

⇒ S = (1/3 - 1/3²⁰²³) : 2/3

= (1 - 1/3²⁰²²) : 2

Lại có: 1 - 1/3²⁰²² < 1

⇒ S < 1/2

S= \((\dfrac{1}{2}-\dfrac{1}{2\times3^{2022}})\)

?

a) Ta có:

Suy ra: 

Do đó .

Lại có .

Vậy A < B.

\(B=\left(\dfrac{2020}{2}+1\right)+\left(\dfrac{2019}{3}+1\right)+...+\left(\dfrac{1}{2021}+1\right)+1\)

\(=\dfrac{2022}{2}+\dfrac{2022}{3}+...+\dfrac{2022}{2021}+\dfrac{2022}{2022}\)

=2022(1/2+1/3+...+1/2021+1/2022)

=>B/A=2022

Cứu với ;-;