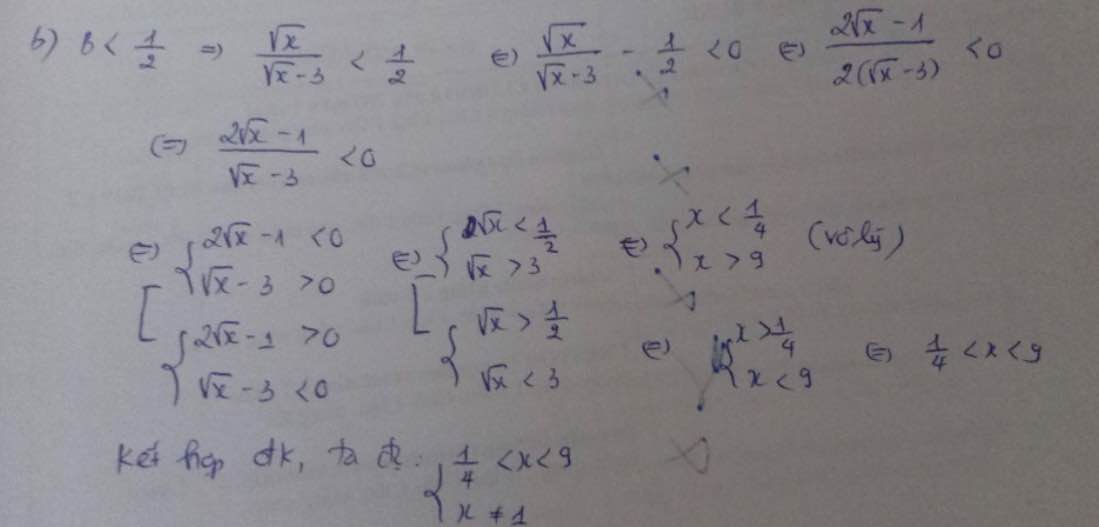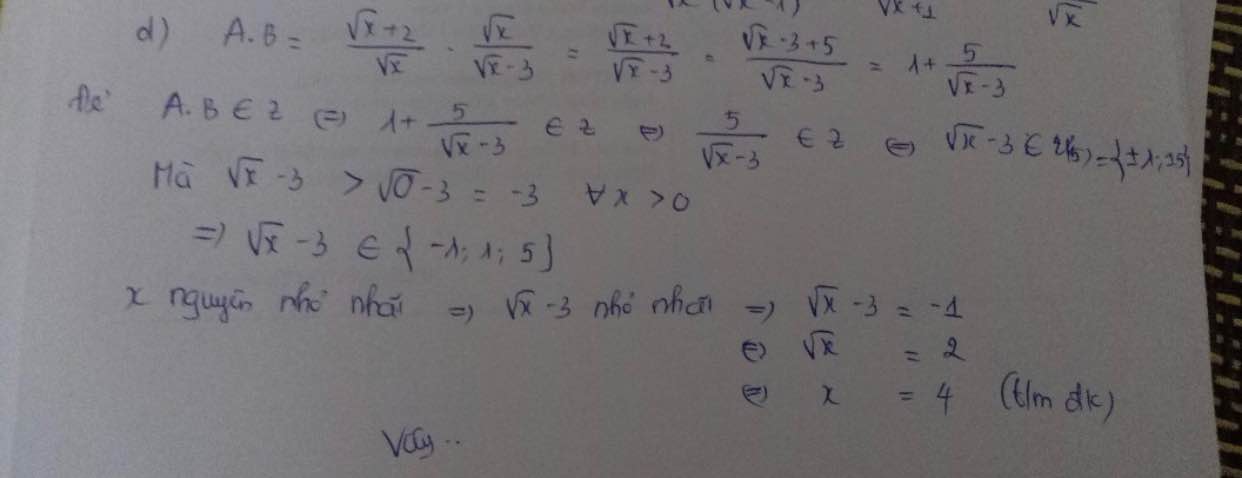mn giúp câu d với

Những câu hỏi liên quan
 Câu d khá khó mn giúp em với
Câu d khá khó mn giúp em với
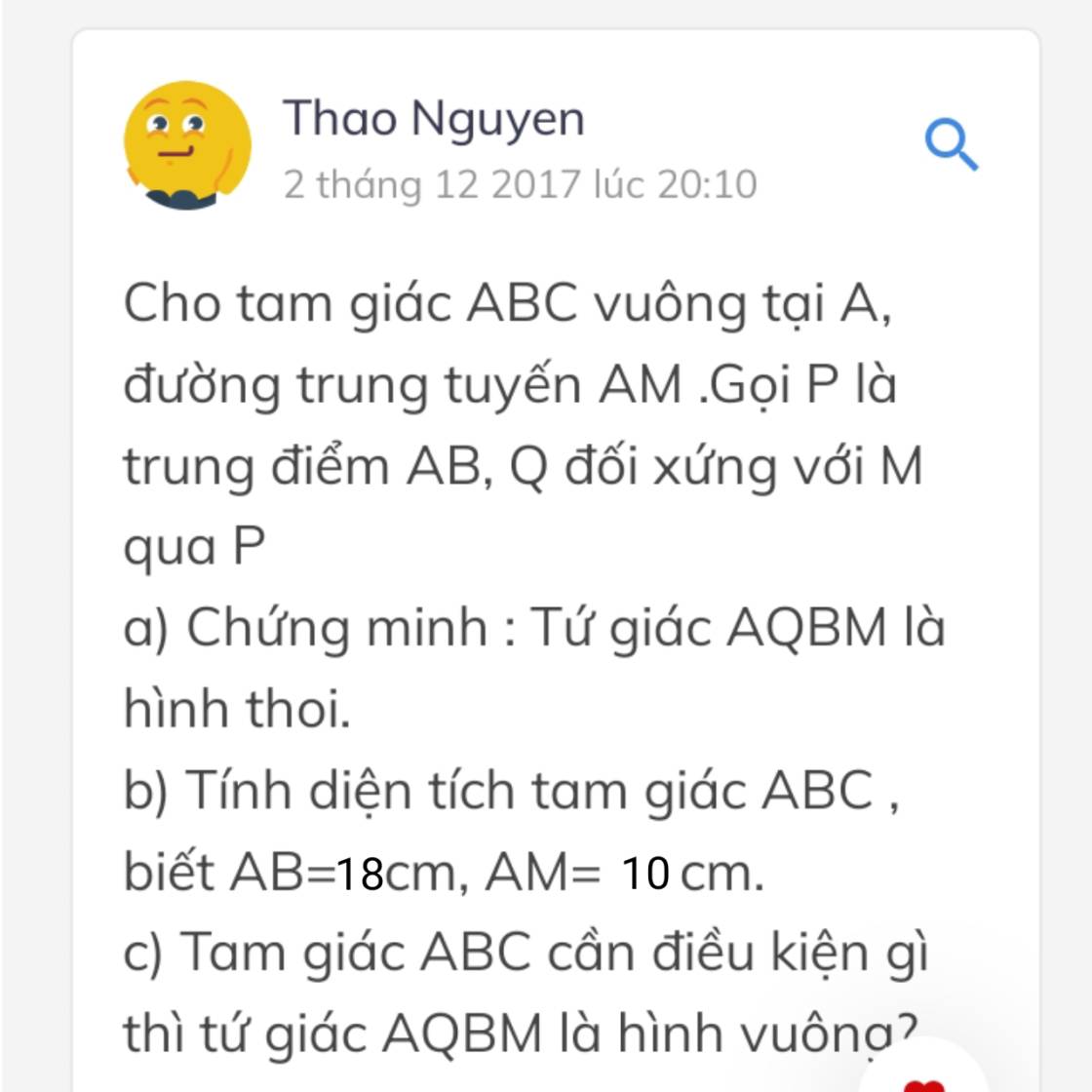
a: Xét ΔABC có
D là trung điểm của AB
E là trung điểm của AC
Do đó: DE là đường trung bình của ΔABC
Suy ra: DE//BC và \(DE=\dfrac{BC}{2}\)(1)
Xét tứ giác BDEC có DE//BC
nên BDEC là hình thang
b: Ta có: F là trung điểm của BC
nên \(FB=\dfrac{BC}{2}\left(2\right)\)
Từ (1) và (2) suy ra DE//BF và DE=BF
hay DEFB là hình bình hành
Đúng 1
Bình luận (0)
\(a,\) Ta có \(AD=BD;AE=EC\) nên \(DE\) là đường trung bình \(\Delta ABC\)
\(\Rightarrow\left\{{}\begin{matrix}DE//BC\\DE=\dfrac{1}{2}BC\end{matrix}\right.\Rightarrow DEFB\) là hình thang
\(b,\) Ta có \(DE=\dfrac{1}{2}BC=BF=FC\) (F là trung điểm BC)
\(DE//BC\Rightarrow DE//BF\)
\(\Rightarrow DEFB\) là hình bình hành
\(c,\) Ta có \(DEFB\) là hbh, \(O\) là trung điểm DF
\(\Rightarrow O\) là trung điểm \(BE\Rightarrow O,B,E\) thẳng hàng
\(d,\) Gọi \(G\) là trung điểm MC
Ta có \(AE=EC;MG=GC\Rightarrow EG\) là đtb \(\Delta AMC\)
\(\Rightarrow EG//AM\Rightarrow EG//OM\)
Mà \(BO=OE\Rightarrow BM=MG\)
\(\Rightarrow BM=MG=GC\Rightarrow BM=\dfrac{1}{3}BC\)
Đúng 2
Bình luận (0)
GIÚP EM CÂU D BÀI 6 VỚI MN
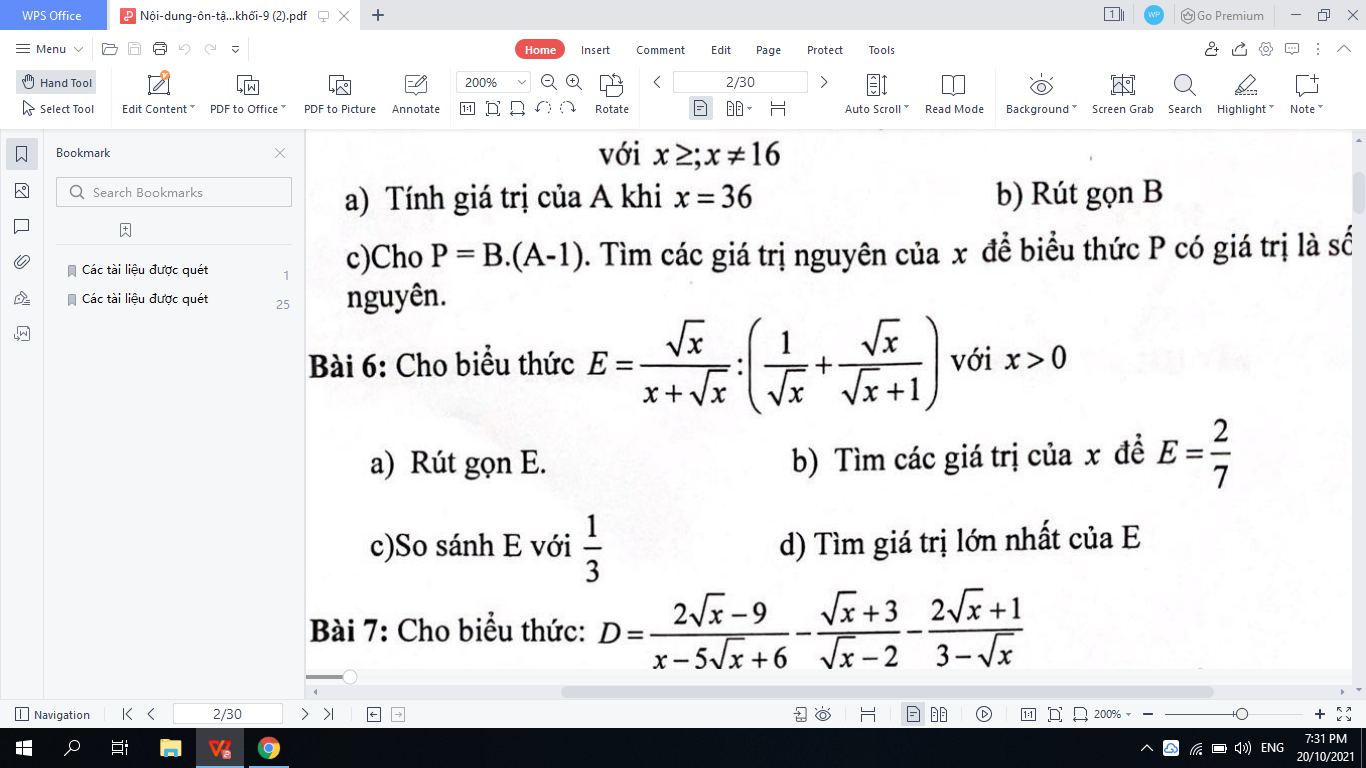
Bài 6:
a: Ta có: \(E=\dfrac{1}{\sqrt{x}+1}:\left(\dfrac{1}{\sqrt{x}}+\dfrac{\sqrt{x}}{\sqrt{x}+1}\right)\)
\(=\dfrac{1}{\sqrt{x}+1}\cdot\dfrac{\sqrt{x}\left(\sqrt{x}+1\right)}{x+\sqrt{x}+1}\)
\(=\dfrac{\sqrt{x}}{x+\sqrt{x}+1}\)
Đúng 0
Bình luận (0)
Mn giúp mik câu c và d với
gửi muộn thế, trưa rùi, ko ai giúp đâu :>
Đúng 1
Bình luận (0)
c: =>4(2x+2)+6>5(3x-2)
=>8x+8+6>15x-10
=>8x+14>15x-10
=>-7x>-24
hay x<24/7
d: =>3(2x+1)-5(2x-2)>225
=>6x+3-10x+10>225
=>-4x+13>225
=>-4x>212
hay x<-53
Đúng 1
Bình luận (0)
mn giúp em câu c và d với ạ!!

$A=x-3\sqrt{x}+1=(x-3\sqrt{x}+\frac{9}{4})-\frac{5}{4}$
$=(\sqrt{x}-\frac{3}{2})^2-\frac{5}{4}$
$\geq \frac{-5}{4}$
Vậy $A_{\min}=-\frac{5}{4}$. Giá trị này đạt tại $\sqrt{x}-\frac{3}{2}=0\Leftrightarrow x=\frac{9}{4}$
----------------
$B=\frac{3\sqrt{x}-1}{\sqrt{x}+2}=3-\frac{5}{\sqrt{x}+2}$
Vì $\sqrt{x}\geq 0$ nên $\sqrt{x}+2\geq 2$
$\Rightarrow \frac{5}{\sqrt{x}+2}\leq \frac{5}{2}$
$\Rightarrow B\geq 3-\frac{5}{2}=\frac{1}{2}$
Vậy $B_{\min}=\frac{1}{2}$ khi $x=0$
Đúng 1
Bình luận (0)
$C=\frac{\sqrt{x}(\sqrt{x}+3)-3(\sqrt{x}+3)+19}{\sqrt{x}+3}$
$=\sqrt{x}-3+\frac{19}{\sqrt{x}+3}$
$=(\sqrt{x}+3)+\frac{19}{\sqrt{x}+3}-6$
$\geq 2\sqrt{19}-6$ theo BĐT Cô-si
Dấu "=" xảy ra khi $(\sqrt{x}+3)^2=19\Leftrightarrow x=28-6\sqrt{19}$
Đúng 1
Bình luận (0)
$D=\frac{\sqrt{x}(\sqrt{x}-1)-2(\sqrt{x}-1)+1}{\sqrt{x}-1}$
$=\sqrt{x}-2+\frac{1}{\sqrt{x}-1}$
$=(\sqrt{x}-1)+\frac{1}{\sqrt{x}-1}-1$
$\geq 2-1=1$ theo BĐT Cô-si
Vậy $D_{\min}=1$. Dấu "=" xảy ra khi $(\sqrt{x}-1)^2=1$
$\Leftrightarrow x=4$
Đúng 1
Bình luận (0)

Mn giúp e làm câu 1 phần D với
1 across
2 far
3 crossroad
4 reason
5 safest
6 only
7 vehicles
8 follow
Đúng 3
Bình luận (0)
Em còn mỗi câu d thôi mn giúp e với
Lời giải:
d.
Áp dụng định lý Menelaus cho tam giác $BDF$ có $A,O,M$ lần lượt thuộc $BD, DF, BF$ và $A,O,M$ thẳng hàng:
$\frac{MF}{MB}.\frac{OD}{OF}.\frac{AB}{AD}=1$
$\Leftrightarrow \frac{MF}{MB}.1.2=1$
$\Leftrightarrow \frac{MF}{MB}=\frac{1}{2}$
$\Rightarrow \frac{BF}{MB}=\frac{3}{2}$
$\Leftrightarrow \frac{BC}{2MB}=\frac{3}{2}$
$\Leftrightarrow BC=3MB$ (đpcm)
Đúng 1
Bình luận (0)
 Em cần giúp câu c và d ạ, mn giúp em với em đang cần gấp
Em cần giúp câu c và d ạ, mn giúp em với em đang cần gấp
b) Áp dụng hệ thức lượng trong tam giác vuông vào ΔAHB vuông tại H có HM là đường cao ứng với cạnh huyền AB, ta được:
\(AM\cdot AB=AH^2\)(1)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔAHC vuông tại H có HN là đường cao ứng với cạnh huyền AC, ta được:
\(AN\cdot AC=AH^2\)(2)
Từ (1) và (2) suy ra \(AM\cdot AB=AN\cdot AC\)
Đúng 0
Bình luận (0)
Mn giúp em câu b,d với ạ. Em cần gấp
a) Thay x=36 vào B, ta được:
\(B=\dfrac{6}{6-3}=\dfrac{6}{3}=2\)
b) Để \(B< \dfrac{1}{2}\) thì \(B-\dfrac{1}{2}< 0\)
\(\Leftrightarrow\dfrac{\sqrt{x}}{\sqrt{x}-3}-\dfrac{1}{2}< 0\)
\(\Leftrightarrow\dfrac{2\sqrt{x}-\sqrt{x}+3}{2\left(\sqrt{x}-3\right)}< 0\)
\(\Leftrightarrow\dfrac{\sqrt{x}+3}{2\left(\sqrt{x}-3\right)}< 0\)
\(\Leftrightarrow\sqrt{x}-3< 0\)
\(\Leftrightarrow x< 9\)
Kết hợp ĐKXĐ, ta được: \(0\le x< 9\)
Đúng 0
Bình luận (0)
c) Ta có: \(A=\left(\dfrac{\sqrt{x}}{\sqrt{x}-1}-\dfrac{1}{x-\sqrt{x}}\right):\dfrac{\sqrt{x}+1}{\sqrt{x}+2}\)
\(=\dfrac{x-1}{\sqrt{x}\left(\sqrt{x}-1\right)}\cdot\dfrac{\sqrt{x}+2}{\sqrt{x}+1}\)
\(=\dfrac{\sqrt{x}+2}{\sqrt{x}}\)
d) Ta có: P=AB
nên \(P=\dfrac{\sqrt{x}+2}{\sqrt{x}}\cdot\dfrac{\sqrt{x}}{\sqrt{x}-3}=\dfrac{\sqrt{x}+2}{\sqrt{x}-3}\)
Để P nguyên thì \(\sqrt{x}+2⋮\sqrt{x}-3\)
\(\Leftrightarrow5⋮\sqrt{x}-3\)
\(\Leftrightarrow\sqrt{x}-3=-1\)(Vì x nhỏ nhất)
\(\Leftrightarrow\sqrt{x}=2\)
hay x=4
Đúng 0
Bình luận (0)
MN ơi giúp mình với còn câu d) chưa làm đc thôi