a: Xét ΔABC có
D là trung điểm của AB
E là trung điểm của AC
Do đó: DE là đường trung bình của ΔABC
Suy ra: DE//BC và \(DE=\dfrac{BC}{2}\)(1)
Xét tứ giác BDEC có DE//BC
nên BDEC là hình thang
b: Ta có: F là trung điểm của BC
nên \(FB=\dfrac{BC}{2}\left(2\right)\)
Từ (1) và (2) suy ra DE//BF và DE=BF
hay DEFB là hình bình hành
\(a,\) Ta có \(AD=BD;AE=EC\) nên \(DE\) là đường trung bình \(\Delta ABC\)
\(\Rightarrow\left\{{}\begin{matrix}DE//BC\\DE=\dfrac{1}{2}BC\end{matrix}\right.\Rightarrow DEFB\) là hình thang
\(b,\) Ta có \(DE=\dfrac{1}{2}BC=BF=FC\) (F là trung điểm BC)
\(DE//BC\Rightarrow DE//BF\)
\(\Rightarrow DEFB\) là hình bình hành
\(c,\) Ta có \(DEFB\) là hbh, \(O\) là trung điểm DF
\(\Rightarrow O\) là trung điểm \(BE\Rightarrow O,B,E\) thẳng hàng
\(d,\) Gọi \(G\) là trung điểm MC
Ta có \(AE=EC;MG=GC\Rightarrow EG\) là đtb \(\Delta AMC\)
\(\Rightarrow EG//AM\Rightarrow EG//OM\)
Mà \(BO=OE\Rightarrow BM=MG\)
\(\Rightarrow BM=MG=GC\Rightarrow BM=\dfrac{1}{3}BC\)

 Câu d khá khó mn giúp em với
Câu d khá khó mn giúp em với




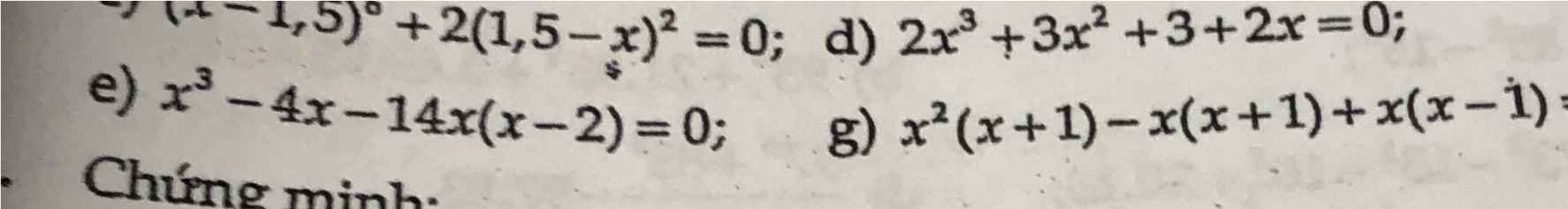

 Mn giúp em bài 3 câu bc với em tính số xấu quá, mong mn giúp ạ:(
Mn giúp em bài 3 câu bc với em tính số xấu quá, mong mn giúp ạ:(

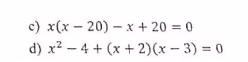 Mn giúp em 2 câu này với
Mn giúp em 2 câu này với






