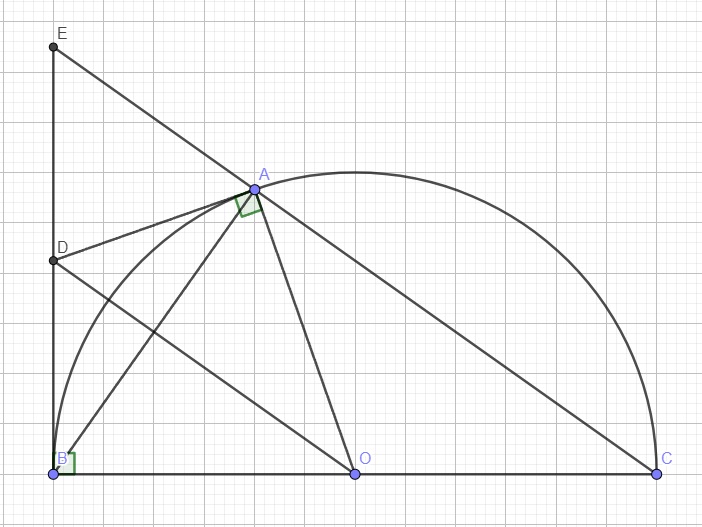
Điểm A thuộc nửa đường tròn ( O;6cm) đường kính BC sao cho diện tích tam giác ABC lớn nhất. Khi đó ,số đo cung AC là A. 60° B.45°

Những câu hỏi liên quan
cho nửa đường tròn tâm O có đường kínhAB bằng 2r kẻ hai tiếp tuyến Ax By của nửa O tại A và B Ax By và nửa đường tròn O thuộc cùng một nửa mặt phẳng có bờ là đường thẳng AB qua điểm M thuộc nửa đường tròn M khác A B kẻ tiếp tuyến với nửa đường tròn cắt tia Ax By theo thứ tự tại C Da chứng minh AC + BD CD và tam giác BCD vuông tại Ob Tính tích AC nhân BD theo ABc các đường thẳng AB và BC cắt nhau tại N Chứng minh MN vuông góc với AB
Đọc tiếp
cho nửa đường tròn tâm O có đường kínhAB bằng 2r kẻ hai tiếp tuyến Ax By của nửa O tại A và B Ax By và nửa đường tròn O thuộc cùng một nửa mặt phẳng có bờ là đường thẳng AB qua điểm M thuộc nửa đường tròn M khác A B kẻ tiếp tuyến với nửa đường tròn cắt tia Ax By theo thứ tự tại C D
a chứng minh AC + BD = CD và tam giác BCD vuông tại O
b Tính tích AC nhân BD theo AB
c các đường thẳng AB và BC cắt nhau tại N Chứng minh MN vuông góc với AB
Cho nửa đường tròn tâm O có đường kính AB 2R. Kẻ hai tiếp tuyến Ax, By của nửa đường tròn (O) tại A và B (Ax, By và nửa đường tròn thuộc cùng một nửa mặt phẳng có bờ là đường thẳngAB). Qua điểm M thuộc nửa đường tròn (M khác A và B), kẻ tiếp tuyến với nửa đường tròn, cắt tia Ax và By theo thứ tự tại C và D.a) Chứng minh tam giác COD vuông tại 0;b) Chứng minh AC.BDR^2;c) trên tia Cx lấy điểm N sao cho AC CN , chứng minh CO // NM .
Đọc tiếp
Cho nửa đường tròn tâm O có đường kính AB = 2R. Kẻ hai tiếp tuyến Ax, By của nửa đường tròn (O) tại A và B (Ax, By và nửa đường tròn thuộc cùng một nửa mặt phẳng có bờ là đường thẳng
AB). Qua điểm M thuộc nửa đường tròn (M khác A và B), kẻ tiếp tuyến với nửa đường tròn, cắt tia Ax và By theo thứ tự tại C và D.
a) Chứng minh tam giác COD vuông tại 0;
b) Chứng minh AC.BD=R^2;
c) trên tia Cx lấy điểm N sao cho AC = CN , chứng minh CO // NM .
a: Xét (O) có
CM là tiếp tuyến
CA là tiếp tuyến
Do đó: CM=CA và OC là tia phân giác của góc MOA(1)
Xét (O) có
DM là tiếp tuyến
DB là tiếp tuyến
Do đó: DM=DB và OD là tia phân giác của góc MOB(2)
Từ (1) và (2) suy ra \(\widehat{COD}=\dfrac{1}{2}\cdot\left(\widehat{MOA}+\widehat{MOB}\right)=\dfrac{1}{2}\cdot180^0=90^0\)
b: Xét ΔCOD vuông tại O có OM là đường cao
nên \(CM\cdot MD=OM^2=R^2\)
hay \(AC\cdot BD=R^2\)
Đúng 0
Bình luận (0)
Cho nửa đường tròn tâm O có đường kính AB 2R. Kẻ hai tiếp tuyến Ax, By của nửa đường tròn (O) tại A và B (Ax, By và nửa đường tròn thuộc cùng một nửa mặt phẳng có bờ là đường thẳng AB). Qua điểm M thuộc nửa đường tròn (M khác A và B), kẻ tiếp tuyến với nửa đường tròn, cắt tia Ax và By theo thứ tự tại C và D.
a, CM : góc COD 90o
b, CM : CD AC + BD
c, gọi H là hình chiếu của M trên AB , I là giao điểm BC và MH . CM : IM IH
Đọc tiếp
Cho nửa đường tròn tâm O có đường kính AB = 2R. Kẻ hai tiếp tuyến Ax, By của nửa đường tròn (O) tại A và B (Ax, By và nửa đường tròn thuộc cùng một nửa mặt phẳng có bờ là đường thẳng AB). Qua điểm M thuộc nửa đường tròn (M khác A và B), kẻ tiếp tuyến với nửa đường tròn, cắt tia Ax và By theo thứ tự tại C và D.
a, CM : góc COD = 90o
b, CM : CD = AC + BD
c, gọi H là hình chiếu của M trên AB , I là giao điểm BC và MH . CM : IM = IH
Bạn có thể tham khảo bài tương tự ở đây:
BT: Cho nửa đường tròn (O;R) đường kính AB. Kẻ 2 tiếm tuyến Ax, By của nửa đường tròn (O). Qua M thuộc nửa đường tròn (... - Hoc24
Đúng 0
Bình luận (0)
CM góc COD = 90 độ
Theo tính chất 2 tiếp tuyến cắt nhau
Ta có : OC là phân giác góc AOM
=> góc COM = 1/2 góc AOM
OD là phân giác góc BOM
=> góc DOM = 1/2 góc BOM
=> góc COD = góc COM + góc DOM = 1/2 ( góc AOM + góc BOM ) = 1/2 góc AOB = 1/2 x 180 độ = 90 độ
Đúng 0
Bình luận (0)
CM CD = AC + BD
Theo tính chất của 2 tiếp tuyến cắt nhau ta có :
AC = CM
BD = MD
=> CD = MC + MD hay
CD = AC + BD
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
2) Cho điểm M thuộc nửa đường tròn (O; R) đường kính AB. Trên nửa mặt phẳng bờ AB chứa điểm M, kẻ các tia tiếp tuyến Ax, By với nửa đường tròn. Tiếp tuyến tại M của nửa đường tròn cắt tia Ax tại C.a) Chứng minh rằng 4 điểm A, C, O, M cùng thuộc một đường tròn. Chỉ rõ tâm đường đó.b) Tiếp tuyến tại M cắt tia By tại D. Chứng minh rằng AC + BD CD và ACOD vuông tại O.c) Gọi E là giao điểm của AD và BC, K là giao điểm của ME và AB. Chứng minh rằng E là trung điểm MK.
Đọc tiếp
2) Cho điểm M thuộc nửa đường tròn (O; R) đường kính AB. Trên nửa mặt phẳng bờ AB chứa điểm M, kẻ các tia tiếp tuyến Ax, By với nửa đường tròn. Tiếp tuyến tại M của nửa đường tròn cắt tia Ax tại C.
a) Chứng minh rằng 4 điểm A, C, O, M cùng thuộc một đường tròn. Chỉ rõ tâm đường đó.
b) Tiếp tuyến tại M cắt tia By tại D. Chứng minh rằng AC + BD = CD và ACOD vuông tại O.
c) Gọi E là giao điểm của AD và BC, K là giao điểm của ME và AB. Chứng minh rằng E là trung điểm MK.
a: Xét tứ giác CAOM có góc CAO+góc CMO=180 độ
nên CAOM là tứ giác nội tiếp
Tâm là trung điểm của OC
b: Xét (O) có
CM,CA là các tiếp tuyến
nên CM=CA và OC là phân giác của góc MOA(1)
Xét (O) có
DM,DB là các tiếp tuyến
nên DM=DB và OD là phân giác của góc MOB(2)
Từ (1), (2) suy ra góc COD=1/2*180=90 độ
AC+BD=CM+MD=CD
Đúng 0
Bình luận (0)
Bài 15. Cho điểm N thuộc nửa (O; R) đường kính AB. Trên nửa mặt phẳng bờ AB chưa điểm N, kẻ các tia tiếp tuyến Ax, By với nửa đường tròn. Tiếp tuyến tại N của nửa đường tròn cắt tia Ax tại C. a) CMR: A, C, O, N cùng thuộc 1 đường tròn. Chỉ rõ tâm b) Tiếp tuyến tại N cắt tia By tại D Em cần gấp và cho em xin hình
a: góc CAO+góc CNO=90+90=180 độ
=>CAON nội tiếp đường tròn đường kính CO
Tâm là trung điểm của OC
Đúng 1
Bình luận (0)
Cho nửa đường tròn tâm O đường kính AB bằng 2r kẻ hai tiếp tuyến Ax By của mỗi đường tròn tâm O tại b và a (Ax , By phân nửa đường tròn thuộc cùng một mặt phẳng có bờ là đường thẳng AB) qua điểm M thuộc nửa đường tròn (Khác A và B) tiếp tuyến với nửa đường tròn cắt tia Ox và Oy theo thứ tự tại C và D
chứng minh tam giác COD có góc A bằng 90 độ
Chứng minh AC x BC r Bình
Kẻ MH vuông góc với AD E thuộc AC Chứng minh rằng BC đi qua trung điểm của MH
Đọc tiếp
Cho nửa đường tròn tâm O đường kính AB bằng 2r kẻ hai tiếp tuyến Ax By của mỗi đường tròn tâm O tại b và a (Ax , By phân nửa đường tròn thuộc cùng một mặt phẳng có bờ là đường thẳng AB) qua điểm M thuộc nửa đường tròn (Khác A và B) tiếp tuyến với nửa đường tròn cắt tia Ox và Oy theo thứ tự tại C và D
chứng minh tam giác COD có góc A bằng 90 độ
Chứng minh AC x BC = r Bình
Kẻ MH vuông góc với AD E thuộc AC Chứng minh rằng BC đi qua trung điểm của MH
Bài 4: Cho nửa đường tròn (O;R) đường kính BC. Trên nửa mặt phẳng bờ BC chứa nửa đường trònvẽ tiếp tuyến Bx của(O), A là điểm bất kì thuộc nửa đường tròn sao cho AB Tiếp tuyến tại A của (O) cắt tia Bx tại D.a) Chứng minh bốn điểm A,D,B,O cùng thuộc một đường tròn;AB tại điểmK.b) Tia CA cắt Bx tại E. Chứng minh rằng ODsong song CEvà CA.CE4R;
Đọc tiếp
Bài 4: Cho nửa đường tròn (O;R) đường kính BC. Trên nửa mặt phẳng bờ BC chứa nửa đường tròn
vẽ tiếp tuyến Bx của(O), A là điểm bất kì thuộc nửa đường tròn sao cho AB Tiếp tuyến tại A của (O) cắt tia Bx tại D.
a) Chứng minh bốn điểm A,D,B,O cùng thuộc một đường tròn;
AB tại điểm
K.
b) Tia CA cắt Bx tại E. Chứng minh rằng OD
song song CE
và CA.CE=4R;
a: Xét tứ giác ADBO có
\(\widehat{DBO}+\widehat{DAO}=90^0+90^0=180^0\)
=>ADBO là tứ giác nội tiếp
=>A,D,B,O cùng thuộc một đường tròn
b: Xét (O) có
ΔBAC nội tiếp
BC là đường kính
Do đó: ΔBAC vuông tại A
=>BA\(\perp\)AC tại A
=>BA\(\perp\)CE tại A
Xét (O) có
DA,DB là các tiếp tuyến
DO đó: DA=DB
=>D nằm trên đường trung trực của AB(1)
ta có: OA=OB
=>O nằm trên đường trung trực của AB(2)
Từ (1),(2) suy ra OD là đường trung trực của AB
=>OD\(\perp\)AB
Ta có: OD\(\perp\)AB
CE\(\perp\)AB
Do đó: OD//CE
Xét ΔEBC vuông tại B có BA là đường cao
nên \(CA\cdot CE=CB^2\)
=>\(CA\cdot CE=\left(2R\right)^2=4R^2\)
Đúng 1
Bình luận (0)
Cho nửa đường tròn tâm O có đường kính AB2R. Kẻ hai tiếp tuyến Ax,By của nửa đường tròn (O) tại A và B (Ax,By và nửa đường tròn thuộc cùng một nửa mặt phẳng có bờ là đường thẳng AB).Qua điểm M thuộc nửa đường tròn (M khác A và B), kẻ tiếp tuyến với nửa đường tròn, cắt tia Ax và By theo thứ tự tại C và D.
1.chứng minh tam giác COD vuông tại O;
2.chứng minh AC.BDR²;
3.kẻ MH vuông AB (H thuộc AB).chứng minh rằng BC đi qua trung điểm của đoạn MH-
Đọc tiếp
Cho nửa đường tròn tâm O có đường kính AB=2R. Kẻ hai tiếp tuyến Ax,By của nửa đường tròn (O) tại A và B (Ax,By và nửa đường tròn thuộc cùng một nửa mặt phẳng có bờ là đường thẳng AB).Qua điểm M thuộc nửa đường tròn (M khác A và B), kẻ tiếp tuyến với nửa đường tròn, cắt tia Ax và By theo thứ tự tại C và D. 1.chứng minh tam giác COD vuông tại O; 2.chứng minh AC.BD=R²; 3.kẻ MH vuông AB (H thuộc AB).chứng minh rằng BC đi qua trung điểm của đoạn MH-
1: Xét (O) có
CM,CA là tiếp tuyến
nen CM=CA và OC là phân giác của góc MOA(1)
Xét (O) có
DM,DB là tiếp tuyến
nên DM=DB và OD là phân giác của góc MOB(2)
Từ (1), (2) suy ra góc COD=1/2*180=90 độ
2: AC*BD=MC*MD=OM^2=R^2
Đúng 0
Bình luận (0)
:. Cho nửa đường tròn (O), đường kính AB 2R. Gọi Ax, By là các tia vuông góc với AB (Các tia Ax, By và nửa đường tròn thuộc cùng một nửa mặt phẳng bờ AB). Qua điểm I thuộc nửa đường tròn (I khác A và B) kẻ tiếp tuyến với nửa đường tròn (O), nó cắt các tia Ax, By lần lượt ở M và N. a) Chứng minh:góc MON90 độ b) Chứng minh : MN AM + BN. c) Chứng minh AB là tiếp tuyến của đường tròn đường kính MN. d) Xác định vị trí của điểm I trên nửa đường tròn (O) để diện tích tứ giác...
Đọc tiếp
:. Cho nửa đường tròn (O), đường kính AB = 2R. Gọi Ax, By là các tia vuông góc với AB (Các tia Ax, By và nửa đường tròn thuộc cùng một nửa mặt phẳng bờ AB). Qua điểm I thuộc nửa đường tròn (I khác A và B) kẻ tiếp tuyến với nửa đường tròn (O), nó cắt các tia Ax, By lần lượt ở M và N.
a) Chứng minh:góc MON=90 độ
b) Chứng minh : MN = AM + BN.
c) Chứng minh AB là tiếp tuyến của đường tròn đường kính MN.
d) Xác định vị trí của điểm I trên nửa đường tròn (O) để diện tích tứ giác AMNB đạt giá trị nhỏ nhất.
a: Xét (O) có
MI,MA là tiếp tuyến
nên MI=MA và OM là phân giác của góc AOI(1)
Xét (O) có
NI,NB là tiếp tuyến
nên NI=NB và ON là phân giác của góc IOB(2)
Từ (1), (2) suy ra góc MON=1/2*180=90 độ
b: MN=MI+IN
=>MN=MA+NB
c: Gọi H là trung điểm của MN
Xét hình thang AMNB có
O,H lần lượt là trung điểm của AB,MN
nên HO là đường trung bình
=>HO//AM//BN
=>HO vuông góc AB
=>AB là tiếp tuyến của(H)
Đúng 0
Bình luận (0)
Bài 4: Cho nửa đường tròn (O;R) đường kính BC. Trên nửa mặt phẳng bờ BC chứa nửa đường trònvẽ tiếp tuyến Bx của(O), A là điểm bất kì thuộc nửa đường tròn sao cho AB Tiếp tuyến tại 4 của (O) cắt tia Bx tại D.a) Chứng minh bốn điểm A,D,B,O cùng thuộc một đường tròn;AB tại điểmK.b) Tia CA cắt Bx tại E. Chứng minh rằng ODsong song CEvà CA.CE4R;
Đọc tiếp
Bài 4: Cho nửa đường tròn (O;R) đường kính BC. Trên nửa mặt phẳng bờ BC chứa nửa đường tròn
vẽ tiếp tuyến Bx của(O), A là điểm bất kì thuộc nửa đường tròn sao cho AB Tiếp tuyến tại 4 của (O) cắt tia Bx tại D.
a) Chứng minh bốn điểm A,D,B,O cùng thuộc một đường tròn;
AB tại điểm
K.
b) Tia CA cắt Bx tại E. Chứng minh rằng OD
song song CE
và CA.CE=4R;
a.
Do AD là tiếp tuyến tại A \(\Rightarrow\widehat{OAD}=90^0\)
\(\Rightarrow\) 3 điểm O, A, D thuộc đường tròn đường kính OD (1)
BD là tiếp tuyến tại B \(\Rightarrow\widehat{OBD}=90^0\)
\(\Rightarrow\) 3 điểm O, B, D thuộc đường tròn đường kính OD (2)
(1);(2) \(\Rightarrow\) 4 điểm A, D, B, O cùng thuộc đường tròn đường kính OD
b.
Do D là giao điểm 2 tiếp tuyến tại A và B, theo t/c hai tiếp tuyến cắt nhau
\(\Rightarrow DA=DB\)
Mà \(OA=OB=R\)
\(\Rightarrow OD\) là trung trực của AB \(\Rightarrow OD\perp AB\) (3)
BC là đường kính và A thuộc đường tròn nên \(\widehat{BAC}\) là góc nt chắn nửa đường tròn
\(\Rightarrow\widehat{BAC}=90^0\Rightarrow BA\perp CA\) (4)
(3);(4) \(\Rightarrow OD||CA\) (cùng vuông góc AB) hay \(OD||CE\)
Áp dụng hệ thức lượng trong tam giác vuông BCE với đường cao BA ứng với cạnh huyền:
\(BC^2=CA.CE\Rightarrow\left(2R\right)^2=CA.CE\)
\(\Rightarrow CA.CE=4R^2\)
Đúng 1
Bình luận (2)
Em kiểm tra lại đề bài, đoạn này là sao nhỉ: "Tiếp tuyến tại 4 của (O) "
Đúng 0
Bình luận (4)