Cho ∆ABC.M là điểm nằm trong ∆ABC.Vẽ MD vuông góc BC tại D,ME vuông góc AC tại E,MF vuông góc AB tại F.Chứng minh rằng AF² + BD² + CE² = AE² + BF² + CD²

Những câu hỏi liên quan
cho tam giác ABC. M là điểm nằm trong tam giác đó. Vẽ MD vuông với BC tại D, ME vuôn với AC tại E, MF vuông với AB tại F. Chứng minh AF^2+BD^2+CE^2=AE^2+BF^2+CD^2
Cho M nằm trong tam giác ABC.Vẽ MD vuông góc với BC,ME vuông góc với AC, MF vuông góc với AB
a) CMR:AE^2 + CD^2 + BF^2 = AF^2 +BD^2 +CE^2
b) Xác định vị trí M sao cho AE^2 + CD^2 +BF^2 nhỏ nhất
Cho ΔABC. Lấy điểm M bất kì nằm trong ΔABC. Kẻ MD, ME, MF lần lượt vuông góc với BC, AC, AB tại D, E, F. Chứng minh rằng AF^2 + BD^2 + EC^2 = AE^2 + FB^2 + DC^2.
CHO tam giác ABC cân tại A,M là trung điểm BC
a.chứng minh tam giác AMB=AMC
b.Vẽ ME vuông góc AB TẠI E ,MF vuông góc AC tại F.Chứng minh AM vuông góc AF
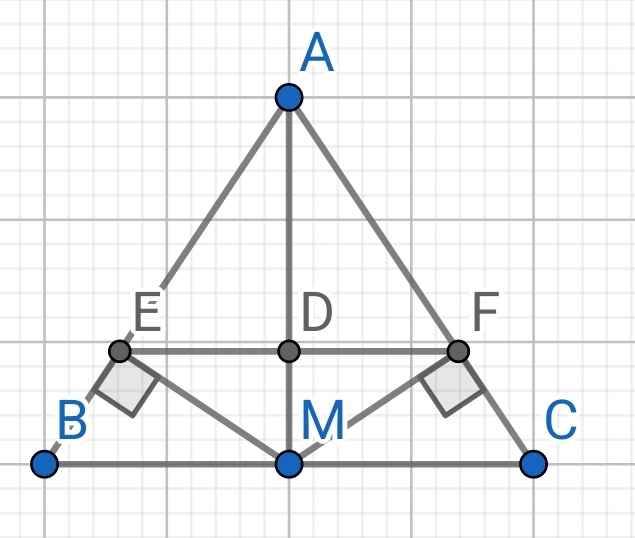 a) Do M là trung điểm của BC (gt)
a) Do M là trung điểm của BC (gt)
⇒ BM = CM
Do ∆ABC cân tại A (gt)
⇒ AB = AC
Xét ∆AMB và ∆AMC có:
AM là cạnh chung
AB = AC (cmt)
BM = CM (cmt)
⇒ ∆AMB = ∆AMC (c-c-c)
b) Sửa đề:
Chứng minh AM EF
Giải:
Gọi D là giao điểm của AM và EF
Do ∆AMB = ∆AMC (cmt)
⇒ ∠MAB = ∠MAC (hai góc tương ứng)
⇒ ∠MAE = ∠MAF
Xét hai tam giác vuông: ∆MAE và ∆MAF có:
AM là cạnh chung
∠MAE = ∠MAF (cmt)
⇒ ∆MAE = ∆MAF (cạnh huyền - góc nhọn)
⇒ AE = AF (hai cạnh tương ứng)
Do ∠MAE = ∠MAF (cmt)
⇒ ∠DAE = ∠DAF
Xét ∆ADE và ∆ADF có:
AD là cạnh chung
∠DAE = ∠DAF (cmt)
AE = AF (cmt)
⇒ ∆ADE = ∆ADF (c-g-c)
⇒ ∠ADE = ∠ADF (hai góc tương ứng)
Mà ∠ADE + ∠ADF = 180⁰ (kề bù)
⇒ ∠ADE = ∠ADF = 180⁰ : 2 = 90⁰
⇒ AD ⊥ EF
Đúng 3
Bình luận (0)
Từ điểm M nằm trong tam giác ABC vẽ MDvuông góc BC tại D, ME vuông góc với AC tại E, MF vuông góc với AB tại F. Trên các tia MD,ME,MF, lằn lượt lấy các điềm I,K,L sao cho MI/BC=MK/AC=MI/AB. Chứng minh rằng M là trọng tâm của tam giác I,K,L
cho tam giác ABC vuông cân tại A. H là trung điểm cạnh BC.M là điểm nằm giữa B và H. Bẽ MD vuông góc AB tại D, ME vuông góc AC tại E .chứng minh rằng : a, AH vuông góc BC
b, ADb= CE , BD = AE
c, MB2 + MC2 = 2MA2
Cho tam giác ABC đều có đường cao AH=h. M là điểm nằm trong tam giác ABC, vẽ MD vuông góc AB tại D , ME vuông góc BC tại E và MF vuông góc AC tại F.
a/ CMR MD+ME+MF=h
b/ xác định vị trí của điểm M trong trường hợp MD=ME=MF
1.Cho tam giác ABC vuông tại A (ABAC)a) Cho biết AB 8cm, BC 10cm. Tính AC.b) Gọi M là trung điểm cạnh BC. Trên tia đối tia MA lấy D sao cho MD MA. Vẽ AH vuông góc BC tại H, trên tia đối của tia HA lấy E sao cjo HEHA. Cứng minh rằng:*CD vuông góc AC *tam giác CAEcân *BDCE *AE vuông góc ED 2.Cho tam giác ABC vuông cân tại A. H là trung điểm cạnh BC. M là điểm nằm giữa B và H. Vẽ MD vuông góc AB tại D, ME vuông góc AC tại E. Chứng minh rằng:a)AH vuông góc...
Đọc tiếp
1.Cho tam giác ABC vuông tại A (AB>AC)
a) Cho biết AB= 8cm, BC= 10cm. Tính AC.
b) Gọi M là trung điểm cạnh BC. Trên tia đối tia MA lấy D sao cho MD =MA. Vẽ AH vuông góc BC tại H, trên tia đối của tia HA lấy E sao cjo HE=HA. Cứng minh rằng:
*CD vuông góc AC *tam giác CAEcân *BD=CE *AE vuông góc ED
2.Cho tam giác ABC vuông cân tại A. H là trung điểm cạnh BC. M là điểm nằm giữa B và H. Vẽ MD vuông góc AB tại D, ME vuông góc AC tại E. Chứng minh rằng:
a)AH vuông góc BC b) AD=CE, BD=AE c) MB2 + MC2 = 2MA2
Mình cần gấp, các bạn giải nhanh và đầy đủ giúp mình nhé, cảm ơn.
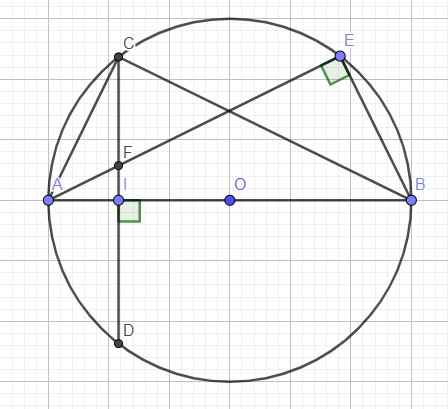
Cho (O) đường kính AB.Vẽ dây CD vuông góc với AB tại I (I nằm giữa A và O).Lấy điểm E trên cung nhỏ BC,AE cắt CD tại F.Chứng minh rằng: a.Tứ giác BEFI nội tiếp b.AE . AF = AC^2
a: Xét (O) có
ΔAEB nội tiếp
AB là đường kính
Do đó: ΔAEB vuông tại E
Xét tứ giác BEFI có
\(\widehat{BEF}+\widehat{BIF}=180^0\)
Do đó: BEFI là tứ giác nội tiếp
b: Xét ΔACE và ΔAFC có
\(\widehat{CAF}\) chung
\(\widehat{AEC}=\widehat{ACF}\)
Do đó: ΔACE\(\sim\)ΔAFC
Suy ra: \(\dfrac{AE}{AC}=\dfrac{AC}{AF}\)
hay \(AE\cdot AF=AC^2\)
Đúng 1
Bình luận (0)
Do E thuộc đường tròn \(\Rightarrow\widehat{AEB}\) là góc nội tiếp chắn nửa đường tròn
\(\Rightarrow\widehat{AEB}=90^0\)
Lại có \(\widehat{FIB}=90^0\) (do \(CD\perp AB\) tại I)
\(\Rightarrow\) E và I cùng nhìn BF dưới 1 góc vuông
\(\Rightarrow\) Tứ giác BEFI nội tiếp đường tròn đường kính BF
b.
Xét hai tam giác vuông AIF và AEB có: góc \(\widehat{IAF}\) chung
\(\Rightarrow\Delta_VAIF\sim\Delta_VAEB\left(g.g\right)\Rightarrow\dfrac{AI}{AE}=\dfrac{AF}{AB}\Rightarrow AI.AB=AE.AF\) (1)
Mặt khác \(\widehat{ACB}\) là góc nội tiếp chắn nửa đường tròn
\(\Rightarrow\Delta ACB\) vuông tại C
Áp dụng hệ thức lượng cho tam giác vuông ACB với đường cao CI:
\(AC^2=AI.AB\) (2)
(1);(2) \(\Rightarrow AE.AF=AC^2\)
Đúng 2
Bình luận (0)