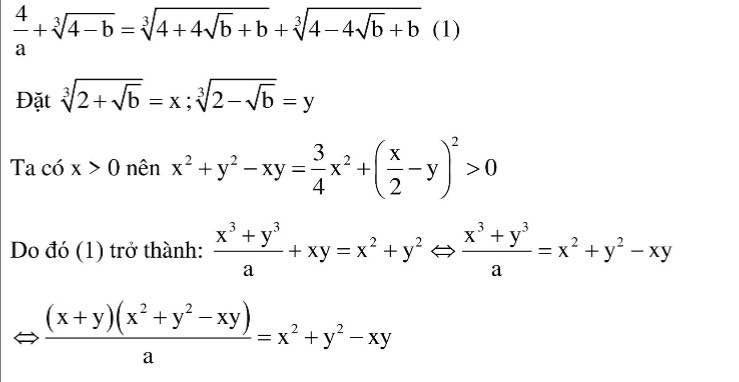Giải phương trình nghiệm nguyên: \(\dfrac{4}{x}+\dfrac{2}{y}=1\)

Những câu hỏi liên quan
Giải phương trình nghiệm nguyên sau
x + \(\dfrac{1}{x}\) + y + \(\dfrac{1}{y}\) = 4
\(x+\dfrac{1}{x}+y+\dfrac{1}{y}=4\)
\(\Rightarrow x+y+\dfrac{x+y}{xy}=4\)
\(\Rightarrow\left(x+y\right)\left(xy+1\right)=4xy\)
Đặt \(\left\{{}\begin{matrix}x+y=u\\xy=v\end{matrix}\right.\) với \(u;v\in Z\) và \(u^2\ge4v\); \(v\ne0\)
\(\Rightarrow u\left(v+1\right)=4v\)
\(\Rightarrow u=\dfrac{4v}{v+1}=4-\dfrac{4}{v+1}\)
\(\Rightarrow v+1=Ư\left(4\right)\Rightarrow v+1=\left\{-4;-2;-1;1;2;4\right\}\)
\(\Rightarrow v=\left\{-5;-3;-2;1;3\right\}\)
\(\Rightarrow u=\left\{5;6;8;2;3\right\}\)
Loại cặp \(\left(u;v\right)=\left(3;3\right)\) không thỏa mãn \(u^2\ge4v\)
Ta được \(\left(u;v\right)=\left(5;-5\right);\left(6;-3\right);\left(8;-2\right);\left(2;1\right)\)
TH1: \(\left\{{}\begin{matrix}x+y=5\\xy=-5\end{matrix}\right.\) không tồn tại x;y nguyên thỏa mãn
TH2: \(\left\{{}\begin{matrix}x+y=6\\xy=-3\end{matrix}\right.\) ko tồn tại x;y nguyên thỏa mãn
TH3: \(\left\{{}\begin{matrix}x+y=8\\xy=-2\end{matrix}\right.\) không tồn tại x;y nguyên thỏa mãn
TH4: \(\left\{{}\begin{matrix}x+y=2\\xy=1\end{matrix}\right.\) \(\Rightarrow x=y=1\)
Vậy pt có đúng 1 cặp nghiệm nguyên \(\left(x;y\right)=\left(1;1\right)\)
Đúng 0
Bình luận (0)
Giải phương trình nghiệm nguyên: y = \(\dfrac{x^2-x+1}{x^2+x+1}\)
Các bn giải theo phương pháp sử dụng đk có nghiệm của phương trình bậc hai giúp mk ạ!
Đúng 1
Bình luận (0)
mình có 1 cách khác nữa:
vì y ∈ Z nên \(\dfrac{x^2-x+1}{x^2+x+1}\) ∈ Z
=>x2-x+1⋮x2+x+1=> x2+x+1 -2x ⋮x2+x+1
=>2x⋮x2+x+1 (1)
Xét hiệu (x2+x+1)-2x=(x-\(\dfrac{1}{2}\))2+\(\dfrac{3}{4}\)>0
=>x2+x+1 > 2x (2)
Từ (1) và (2) kết hợp với 2x và x2+x+1 ∈ Z
=> 2x =0 => x =0 => y=1
Vậy phương trình có nghiệm (x,y) là (0,1)
Đúng 1
Bình luận (0)
Tìm nghiệm nguyên của phương trình \(\dfrac{5}{x}-\dfrac{y}{4}=\dfrac{1}{12}\)
\(\dfrac{5}{x}-\dfrac{y}{4}=\dfrac{1}{12}\Leftrightarrow\dfrac{20-xy}{4x}=\dfrac{1}{12}\Leftrightarrow240-12xy=4x\Leftrightarrow240-12xy-4x=0\Leftrightarrow60-3xy-x=0\Leftrightarrow-3xy-x=-60\Leftrightarrow-x\left(3y+1\right)=60\)Đến đây do x,y nguyên nên bạn lập bảng xét ước nhá, lưu ý 3y + 1 chia 3 dư 1 để bớt trường hợp xét nhá.
Đúng 1
Bình luận (0)
1) Chứng minh rằng: \(x^3-7y=51\) không có nghiệm nguyên
2) Tìm nghiệm nguyên của phương trình \(x^2-5y^2=27\)
3) Tìm nghiệm nguyên dương
a) \(\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}=1\)
b)\(\dfrac{1}{x}+\dfrac{1}{y}=z\)
1) Xét x=7k (k ∈ Z) thì x3 ⋮ 7
Xét x= \(7k\pm1\) thì x3 ⋮ 7 dư 1 hoặc 6.
Xét x=\(7k\pm2\) thì x3 ⋮ 7 dư 1 hoặc 6.
Xét x=\(7k\pm3\)\(\) thì x3 ⋮ 7 dư 1 hoặc 6.
Do vế trái của pt chia cho 7 dư 0,1,6 còn vế phải của pt chia cho 7 dư 2. Vậy pt không có nghiệm nguyên.
3) a, Ta thấy x,y,z bình đẳng với nhau, không mất tính tổng quát ta giả thiết x ≥ y ≥ z > 0 <=> \(\dfrac{1}{x}\le\dfrac{1}{y}\le\dfrac{1}{z}\) ,ta có:
\(1=\dfrac{1}{z}+\dfrac{1}{y}+\dfrac{1}{z}\le\dfrac{3}{z}< =>z\le3\)
Kết luận: nghiệm của pt là ( x;y;z): (6:3:2), (4;4;2), (3;3;3) và các hoán vị của nó (pt này có 10 nghiệm).
Đúng 1
Bình luận (0)
1) Giải hệ phương trình:dfrac{1}{x-2}+dfrac{1}{y-1}2dfrac{2}{x-2}-dfrac{3}{y-1}12) Cho phương trình: ^{x^2}– 2(m + 1)x + 4m 0a,Tìm m để phương trình có hai nghiệm phân biệt x_1,x_2b. Tìm m để hai nghiệm x1, x2 thỏa mãn left(x_1-x_2right)^2-x_1.x_23Giaỉ chi tiết giúp mình 1 chút ạ. Mình cảm ơn
Đọc tiếp
1) Giải hệ phương trình:
\(\dfrac{1}{x-2}+\dfrac{1}{y-1}=2\)
\(\dfrac{2}{x-2}-\dfrac{3}{y-1}=1\)
2) Cho phương trình: \(^{x^2}\)– 2(m + 1)x + 4m = 0
a,Tìm m để phương trình có hai nghiệm phân biệt \(x_1,x_2\)
b. Tìm m để hai nghiệm x1, x2 thỏa mãn \(\left(x_1-x_2\right)^2-x_1.x_2=3\)
Giaỉ chi tiết giúp mình 1 chút ạ. Mình cảm ơn
1, ĐKXĐ:\(x\ne2,y\ne1\)
Đặt `1/(x-2)` = a, `1/(y-1)` = b
\(Hệ.\Leftrightarrow\left\{{}\begin{matrix}a+b=2\\2a-3b=1\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{7}{5}\\b=\dfrac{3}{5}\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}\dfrac{1}{x-2}=\dfrac{7}{5}\\\dfrac{1}{y-1}=\dfrac{3}{5}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}7x-14=5\\3y-3=5\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{19}{7}\\y=\dfrac{8}{3}\end{matrix}\right.\)\(2,\Delta'=\left[-\left(m+1\right)\right]^2-4m=m^2+2m+1-4m=m^2-2m+1=\left(m-1\right)^2\ge0\)
Để pt có 2 nghiệm phân biệt thì \(\Delta'>0\Leftrightarrow\left(m-1\right)^2>0\Leftrightarrow m-1\ne0\Leftrightarrow m\ne1\)
b, Theo Vi-ét:\(\left\{{}\begin{matrix}x_1+x_2=2m+2\\x_1x_2=4m\end{matrix}\right.\)
\(\left(x_1-x_2\right)^2-x_1x_2=3\\ \Leftrightarrow\left(x_1+x_2\right)^2-5x_1x_2=3\\ \Leftrightarrow\left(2m+2\right)^2-5.4m-3=0\\ \Leftrightarrow4m^2+8m+4-20m-3=0\\ \Leftrightarrow4m^2-12m+1=0\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{3+2\sqrt{2}}{2}\\x=\dfrac{3-2\sqrt{2}}{2}\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Bài 1: Giải hệ phương trình sauleft{{}begin{matrix}dfrac{1}{2x-y}+left(x+3yright)dfrac{3}{2}dfrac{4}{2x-y}-5left(x+3yright)-2end{matrix}right.Bài 2: Cho phương trình: x^2+(m-1)x-m^2-20a) CMR: phương trình luôn có 2 nghiệm phân biệt forallmb) Tìm m để biểu thức Aleft(dfrac{x_1}{x_2}right)^3+left(dfrac{x_2}{x_1}right)^3 đạt giá trị lớn nhất.
Đọc tiếp
Bài 1: Giải hệ phương trình sau
\(\left\{{}\begin{matrix}\dfrac{1}{2x-y}+\left(x+3y\right)=\dfrac{3}{2}\\\dfrac{4}{2x-y}-5\left(x+3y\right)=-2\end{matrix}\right.\)
Bài 2: Cho phương trình: x\(^2\)+(m-1)x-m\(^2\)-2=0
a) CMR: phương trình luôn có 2 nghiệm phân biệt \(\forall\)m
b) Tìm m để biểu thức A=\(\left(\dfrac{x_1}{x_2}\right)^3+\left(\dfrac{x_2}{x_1}\right)^3\) đạt giá trị lớn nhất.
Bài 2:
a) Ta có: \(\Delta=\left(m-1\right)^2-4\cdot1\cdot\left(-m^2-2\right)\)
\(=m^2-2m+1+4m^2+8\)
\(=5m^2-2m+9>0\forall m\)
Do đó, phương trình luôn có hai nghiệm phân biệt với mọi m
Đúng 1
Bình luận (0)
Bài 1:
ĐKXĐ \(2x\ne y\)
Đặt \(\dfrac{1}{2x-y}=a;x+3y=b\)
HPT trở thành
\(\left\{{}\begin{matrix}a+b=\dfrac{3}{2}\\4a-5b=-2\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{3}{2}-b\\4\left(\dfrac{3}{2}-b\right)-5b=-2\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{3}{2}-b\\6-9b=-2\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}b=\dfrac{8}{9}\\a=\dfrac{11}{18}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x+3y=\dfrac{8}{9}\\2x-y=\dfrac{18}{11}\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}y=2x-\dfrac{18}{11}\\x+3\left(2x-\dfrac{18}{11}\right)=\dfrac{8}{9}\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{82}{99}\\y=\dfrac{2}{99}\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Tìm nghiệm nguyên của phương trình: \(\dfrac{2016}{x+y}+\dfrac{x}{y+2015}+\dfrac{y}{4031}+\dfrac{2015}{x+2016}=2\)
1. Tìm các số nguyên dương a; b sao cho:dfrac{4}{a} + 3sqrt{4-b} 3sqrt{4+4sqrt{b}+b} + 3sqrt{4-4sqrt{b}+b}2. Giải phương trình nghiệm nguyênx^3-y^3-6x^2+12x27
Đọc tiếp
1. Tìm các số nguyên dương a; b sao cho:
\(\dfrac{4}{a}\) \(+\) 3\(\sqrt{4-b}\) \(=\) 3\(\sqrt{4+4\sqrt{b}+b}\) \(+\) 3\(\sqrt{4-4\sqrt{b}+b}\)
2. Giải phương trình nghiệm nguyên
\(x^3-y^3-6x^2+12x=27\)
đăng câu hỏi kiểu j mà đặng đc lên như thế này đấy
Đúng 0
Bình luận (0)
1.
Đặt \(\sqrt[3]{2+\sqrt{b}}=x;\sqrt[3]{2-\sqrt{b}}=y\)
Do \(x>0\Rightarrow x^2+y^2-xy=\dfrac{3}{4}x^2+\left(\dfrac{1}{2}x-y\right)^2>0\)
\(PT\Leftrightarrow\dfrac{x^3+y^3}{a}+xy=x^2+y^2\Leftrightarrow\dfrac{\left(x+y\right)\left(x^2-xy+y^2\right)}{a}=x^2-xy+y^2\\ \Leftrightarrow\left(x^2-xy+y^2\right)\left(\dfrac{x+y}{a}-1\right)=0\\ \Leftrightarrow\dfrac{x+y}{a}=1\\ \Leftrightarrow\sqrt[3]{2+\sqrt{b}}+\sqrt[3]{2-\sqrt{b}}=a\left(1\right)\\ \Leftrightarrow\left(\sqrt[3]{2+\sqrt{b}}+\sqrt[3]{2-\sqrt{b}}\right)^3=a^3\\ \Leftrightarrow4+3a\sqrt[3]{4-b}=a^3\left(2\right)\\ \Rightarrow4-b=\left(\dfrac{a^3-4}{3a}\right)^3\)
Mặt khác \(b\in \mathbb{Z^+}\)
\(\Rightarrow\left(a^3-4\right)⋮3a\Rightarrow\left(a^3-4\right)⋮a\\ \Rightarrow4⋮a\Rightarrow a\in\left\{1;2;4\right\}\)
Với \(a=1\Rightarrow4-b=1\Rightarrow b=5\)
Với \(a=2;a=4\Rightarrow b\notin \mathbb{Z}\)
Vậy \(\left(a;b\right)=\left(1;5\right)\)
Đúng 2
Bình luận (0)
Xem thêm câu trả lời
a) giải phương trình: 8x-3=5x+12
b) giải bất phương trình sau và biểu diễn tập hợp nghiệm trên trục số: \(\dfrac{8-11x}{4}\)< 13
c) Chứng minh rằng: (\(\dfrac{x}{x^2-36}\)- \(\dfrac{x-6}{x^2+6x}\)): \(\dfrac{2x-6}{x^2+6x}\)+ \(\dfrac{x}{6-x}\)= 1
a:=>3x=15
=>x=5
b: =>8-11x<52
=>-11x<44
=>x>-4
c: \(VT=\left(\dfrac{x^2-\left(x-6\right)^2}{x\left(x+6\right)\left(x-6\right)}\right)\cdot\dfrac{x\left(x+6\right)}{2x-6}+\dfrac{x}{6-x}\)
\(=\dfrac{12x-36}{2x-6}\cdot\dfrac{1}{x-6}-\dfrac{x}{x-6}=\dfrac{6}{x-6}-\dfrac{x}{x-6}=-1\)
Đúng 1
Bình luận (0)